高转差率电动机驱动的游梁式抽油机平衡判定调整方法与流程

本发明涉及游梁式抽油机采油系统平衡调节技术领域，特别涉及高转差率电动机驱动的游梁式抽油机平衡判定调整方法。

背景技术：

游梁式抽油机是主要的采油设备，占总采油设备的90％以上。数以万计的游梁式抽油机完成了我国80％的采油量。据中石油信息研究所的一份《国内外油田地面生产系统节能技术调研》报告称，美国抽油机井系统的效率一般为40％，而我国抽油机系统的效率仅为26％。机采能耗费用占采油成本的比例比较大，其中抽油机平衡不好，平衡调节困难是效率低的主要原因之一。

游梁式抽油机的平衡是通过在抽油机的游梁或者曲柄中加入平衡重利用重物升降改变位能来实现整机平衡。在抽油机的下冲程中，将平衡重从低处向高处举升，储存势能，上冲程时，平衡块下落释放这些势能，协助电动机举升抽油杆柱和液柱，减轻电动机负载和减速器的传递扭矩，缓解电动机载荷不均的现象。

游梁式抽油机平衡判别与调整是采油管理中的一项重要内容。游梁式抽油机通过准确的平衡判定及合理的平衡调整，能够有效的降低能耗，提高效率，减轻冲击，延长设备使用寿命。

为了改进现有的游梁式抽油机系统的效率和性能，采用了高转差率和超高转差率电动机进行驱动。由于高转差率电动机的转子电阻较大，电动机起动转矩有较大提高，则抽油机的启动性能得到改善，装机容量有效降低；高转差率电动机的机械特性较软，遇到冲击载荷时，转速下降，在曲柄惯性作用下，减速器和电动机的扭矩变化趋势较硬特性电动机驱动时平缓，扭矩峰值降低，一定程度上改善了机、杆、泵的配合，能有效提高泵的充满度，有节能效果。

高转差率电动机驱动抽油机的主要特点如下：

(1)高转差率电动机的结构使其具有较好的起动性能、较大的起动转矩和软的机械特性，因此抽油机电动机装机容量可以有效降低。

(2)高转差率电动机的额定效率比普通的电动机低，但是在驱动抽油机运行时，由于机、杆、泵的合理匹配，却具有较高的平均效率。

(3)高转差率电动机驱动抽油机时，若配有专用的控制系统，则抽油机采油系统的无功功率和线损可以有效降低，功率因数有效提高。

(4)对于存在倒发电的抽油机采油系统，高转差率电动机可以有效的降低或者消除到发电状态，能够降低供电容量，减少能量转换过程及其损耗，实现了节能功能。

对于高转差率驱动抽油机时，抽油机游梁的平衡，没有发现有专用的平衡判定方法。因此，从现有的抽油机平衡判定方法分析其适合性。目前常用的平衡准则有三种：准则一，抽油机电动机上、下冲程对外做功相等；准则二，悬点上、下冲程中减速箱曲柄轴峰值扭矩相等；准则三，整个冲程中减速箱曲柄轴扭矩均方根值最小。准则二多用于运行中抽油机平衡状态的检验和调整。电动机的输入电流和功率与减速箱曲柄轴扭矩成正比，其变化规律也相同，加上减速箱输出轴扭矩难以测量，因此常用电流法、功率法和扭矩法代替准则二。按准则二调整平衡时，峰值扭矩最小，但负扭矩最大，准则三反之，准则一介于这两者之间。从对减速箱工作状态的影响来看，无法确定哪个准则更好。对于电动机来说，准则三的均方根扭矩最小，其平衡效果最佳，可以降低抽油机能耗而提高经济效益。现在还没有统一标准来评判这三种平衡准则的效果好坏。

在国内油田抽油机平衡状态的运行维护中，应用最多的是准则二。而相应的抽油机平衡测试的方法主要有电流法、功率法、扭矩曲线法等3种方法。

在油田实际生产管理中，采用电流法判断游梁是否时，通常认为下冲程峰值电流与上冲程峰值电流的比值在85％～100％之间时，即为平衡状态。电流法是最简单、实用的方法，采油现场可以用电流表直接测量和判断，但是会出现虚假平衡，即计算数据显示平衡实则不平衡。对于平衡块的调整没有具体计算量，大多时候依靠经验，则很难保证一次准确调整至最佳平衡位置。采用功率法进行平衡判定时，如果下冲程电机峰值功率与上冲程峰值功率的比值在80％～100％之间，则认为抽油机处于平衡状态。扭矩曲线需要分别找出抽油机上、下冲程中曲柄扭矩的峰值，进行比，如峰值比小于90％，则认为不平衡。

有些学者和工程师认为直接测量抽油机曲柄扭矩很难实现，通过示功图计算其扭矩是可行方法之一，但是计算过程中需要的抽油机结构参数较多，且目前抽油机型号和生产厂家较多，不容易实现。抽油机电动机的输入功率与曲柄扭矩有一定的关系，通过电动机输入功率计算曲柄扭矩比较容易，不需要抽油机的结构参数等。电动机输入功率与曲柄扭矩的计算公式如下：

式中，p为电动机瞬时输入功率，kW；T为曲柄扭矩，N·m；n为电动机转速，r/min；η为传动效率。

从上面的公式可以分析出，在抽油机电动机转速波动不大，可以近似的认为恒定的时候，此方法是比较好的方法之一。但是对于高转差率电动机来说，抽油机运行过程中，电动机转速随着负载的变化而变化，不是一个可以近似的恒定转速，所以此方法不适用于高转差驱动的游梁式抽油机平衡的判断，同样也不适合于抽油机进行变速采油时的平衡判定。

超高转差率电动机的较软的机械特性，与游梁式抽油机周期性交变载荷的适用性，都表明了该电动机比普通电动机驱动具有更大的优越性。但是，高转差率电动机或者超高转差率电动机驱动抽油机时，抽油机曲柄转速不再可以近似认为是恒定，有较大波动，同样对抽油机进行动力学分析时，再认为曲柄转速为常数，则会出现计算错误。将曲柄转速波动因素考虑在内时，则建立的曲柄运动规律的运动微分方程与抽油杆柱振动的波动方程之间有着较强的耦合，其求解较为困难。

因此在陕西省教育厅项目(项目编号2013JK1024)支持下，本发明提出一种适合于高转差率电动机驱动的抽油机或者抽油机变速运行时的平衡判定方法，利用电动机的磁链观测方法计算抽油机电动机的转速，结合抽油机动力学分析，进而得出抽油机曲柄的运动规律，分别计算出抽油机悬点的速度、加速度和位移，以及悬点的载荷，计算出抽油机曲柄扭矩，将上、下冲程的最大扭矩进行比较，其比值作为游梁平衡的判定依据。

技术实现要素：

为了克服上述现有技术的缺陷，本发明的目的在于提供一种高转差率电动机驱动游梁式抽油机的平衡判定方法，利用电动机的矢量控制原理和电动机转速磁链观测方法，计算出抽油机曲柄转速，得到其变化规律，使曲柄运动方程和抽油杆柱的波动方程之间解除耦合关系，再分别对抽油机悬点进行运动学和动力学的分析，基于现有的平衡判定方法基础上，利用得到的曲柄扭矩的上、下冲程的峰值，进行平衡判定。

高转差率电动机驱动游梁式抽油机平衡判定方法，包括以下步骤：

步骤一、计算电动机转速

采用三相交流异步电动机定子电压和电流的磁链观测模型，进行电动机转速的计算，电动机定子电压、电流的磁链观测模型为：

ψ_s＝∫(U_s-I_sR_s)dt

式中，ψ_s为定子磁链，Wb；U_s为定子电压，V；I_s为定子电流，A；R_s为定子电阻，Ω；

在ABC坐标系下，定子电压u_a，u_b，u_c和电流i_a，i_b，i_c可以通过坐标变换得到α-β坐标系下的电压u_α，u_β和电流i_α，i_β：

根据α-β坐标系下的电压，求出定子电压的幅值u_s和相位如下：

同样可以得出定子电流的幅值i_s和相位如下：

α-β坐标系下，磁链分量ψ_α和ψ_β，如下：

ψ_α＝∫(u_α-R_si_α)dt ψ_β＝∫(u_β-R_si_β)dt

定子磁链的幅值ψ_sm和相位ψ_ψ，如下：

由计算得到的定子磁链和定子电流，可以得到异步电动机电磁转矩T_e，如下：

T_e＝p_n(ψ_αi_β-ψ_βi_α)

式中，p_n为极对数；

由以上计算得到的电磁转矩、定子磁链，可以计算出电动机转子转差角速度ω_f，如下：

根据ABC坐标系下的电动机定子电压方程，可以计算出电动机定子同步角速度ω_s，如下：

则，电动机转子机械转速ω，如下：

ω＝(ω_s-ω_f)/p_n

根据电动机在ABC坐标系下的三相电压电流转换到α-β坐标系下，利用定子磁链观测的方法，得出了电动机转速；

步骤二、曲柄轴净扭矩计算

将曲柄作为等效构件，建立等效数学模型，求解减速器曲柄轴净扭矩，曲柄运动规律微分方程如下：

式中M_ed为等效驱动力矩，N·m；M_ef为等效阻力矩，N·m；J_e系统转动惯量，kg·m²；θ为t时刻时曲柄所在位置的转角，rad；

电动机产生的等效驱动力矩M_ed，根据电动机的机械特性曲线得出，即

根据电动机额定参数由下式计算：

ω₀＝2πn₀/60

式中，i_MB为电动机输出轴到减速箱的传动比；η_MB为电动机输出轴到减速箱的传动效率；M_M为电动机在转子角速度为的输出扭矩，N·m；λ_k为电动机最大扭矩与额定扭矩的比；M_H为额定扭矩，N·m；P_H为额定功率，kW；n₀为同步转速，min^-1；n_H为额定转速，min^-1，电动机输出扭矩由皮带传递给减速箱得到的扭矩为抽油机减速箱输出净扭矩M_ed，则减速箱输出轴净扭矩M_ed的计算公式：

M_ed＝T_ei_pη_pi_jη_j

式中，T_e为电动机输出扭矩，N·m；η_p为皮带的传动效率；η_j为减速箱的传动效率；i_p为皮带的传动比；i_j减速箱的传动比；

等效阻力矩由下式计算：

式中为游梁式抽油机扭矩因数，m；PRL为抽油机悬点载荷，N；B_W为抽油机平衡配重，N；M_C为曲柄平衡力矩，N·m；τ为平衡重的滞后角，rad；η_CL为曲柄到悬点的传动效率；k₁为系数，与悬点速度相关；

等效转动惯量J_e的计算：

将由抽油机悬点到电动机转子的所有运动部件的质量和转动惯量依据动能相等的原则转化到减速器的输出轴上，则

式中，J_i为第i个部件的转动惯量，kg·m²；ω_i为第i个部件转动速度，1/s；m_i为第i个部件绕的质量，kg；v_i为第i个部件的质心运动速度，m/s；

根据抽油杆柱的波动方程，用F_i,j表示节点i在j时刻的抽油杆柱的载荷，用PRL表示悬点载荷，进而根据抽油机电动机的运动规律，利用运动学可以得出悬点的速度、加速度和位移，即可以求解悬点载荷；将悬点载荷、扭矩因数、抽油机平衡配重、曲柄平衡力矩、平衡重的滞后角以及曲柄到悬点的传动效率等参数代入曲柄净扭矩计算公式即可；

步骤三、游梁平衡的判定

由计算得到的上、下冲程中曲柄轴净扭矩的最大值进行比作为平衡度，即上、下冲程中的扭矩峰值比，如下：

式中，T_max1、T_max2为上、下冲程中的最大的扭矩值；

如果，ε大于0.7，则游梁式抽油机处于平衡状态；如果ε小于0.7，则需要调整平衡块位置，使其达到调整后平衡。

发明的效果：

1)针对像高转差率电动机驱动游梁式抽油机，在变速运行时，抽油机游梁平衡判定的有效方法。

2)采用电动机定子磁链的观测方法推算电动机转速，得出抽油机曲柄运动规律，使曲柄运动微分方程与抽油杆柱的波动方程解耦。

3)充分利用了电动机矢量控制原理，抽油机运动学和动力学的分析，采用磁链观测的方法得出了抽油机曲柄的运行规律，得出了抽油机悬点的速度、加速度和位移，以及载荷。

4)弥补了曲线扭矩法在抽油机变速运行时，平衡判定的不足。

5)经过实例验证，该方法可行，判定较为准确。

6)准确度高：在无载荷位移传感器使用的情况下，通过电动机定子的观测，进行数据采集处理，提高了数据的可靠性，提高游梁平衡判定的准确度。

7)抗干扰性强：电动机定子的电流电压传感器对数据进行采样的过程中，均设计了抗干扰措施和保护措施，数据真实可靠。

高转差率电动机通过增加转子电阻来提高电动机的转差率，具有机械软特性，当阻力矩增大时动力力矩也随之增大，速度也随之减小。游梁式抽油机具有周期性负载，在高转差率电动机进行驱动时，其转速波动较大。因此，游梁式抽油机曲柄的转角不再均匀变化，不能像低转差电动机驱动时再认为曲柄转速为常数，因此以曲柄转速为常数的游梁式抽油机平衡判定方法不再适用。在此提出通过计算转子转速得到曲柄转角的运动规律，进而计算出曲柄净扭矩，选取扭矩平衡法判定计算游梁平衡度。此方法同样适用于游梁式抽油机变速采油时的游梁平衡判定。

附图说明

图1本发明的实施例中抽油机悬点的速度、加速度和位移示意图。

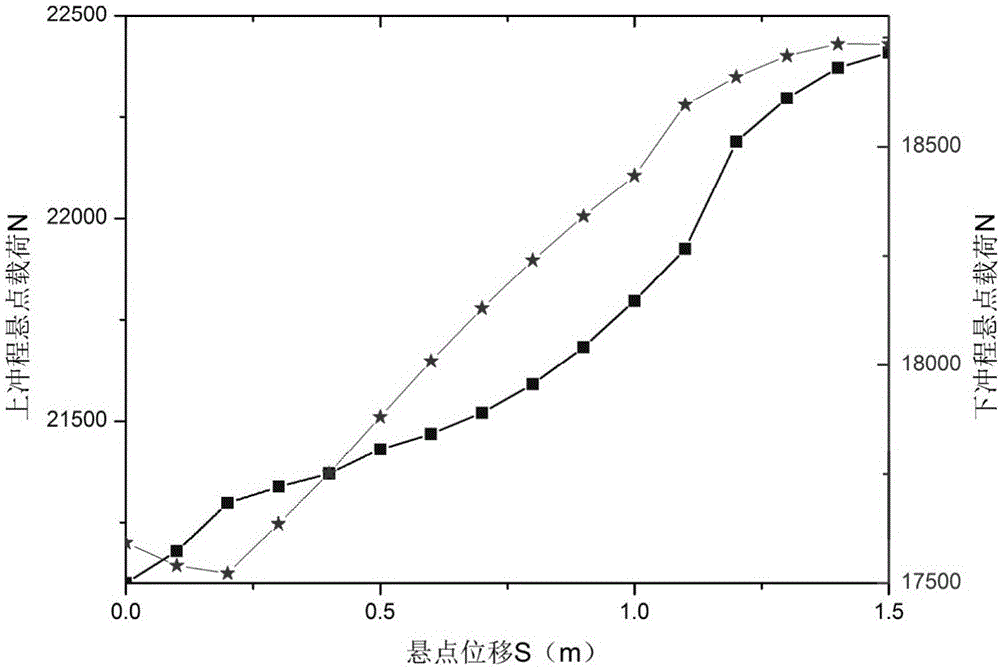
图2本发明的实施例中抽油机上、下冲程的悬点载荷示意图。

图3本发明的实施例中抽油机电动机转速和曲柄净扭矩示意图。

具体实施方式

下面结合附图对本发明做详细叙述。

高转差率电动机驱动游梁式抽油机平衡判定方法，包括以下步骤：

步骤一、计算电动机转速

高转差率电动机在结构与普通三相异步交流电动机的主要区别是高转差率电动机的转子电阻较大。因此，对于普通三相异步交流电动机的定子或者转子的磁链观测方法进行电动机转速的估算，同样适用于高转差率电动机。在此，采用三相交流异步电动机定子电压和电流的磁链观测模型，进行了电动机转速的计算，电动机定子电压、电流的磁链观测模型为：

ψ_s＝∫(U_s-I_sR_s)dt

式中，ψ_s为定子磁链，Wb；U_s为定子电压，V；I_s为定子电流，A；R_s为定子电阻，Ω。

为了计算方便进行了ABC坐标系到α-β坐标系的变换。在ABC坐标系下，定子电压u_a，u_b，u_c和电流i_a，i_b，i_c可以通过坐标变换得到α-β坐标系下的电压u_α，u_β和电流i_α，i_β：

根据α-β坐标系下的电压，求出定子电压的幅值u_s和相位如下：

同样可以得出定子电流的幅值i_s和相位如下：

α-β坐标系下，磁链分量ψ_α和ψ_β，如下：

ψ_α＝∫(u_α-R_si_α)dt ψ_β＝∫(u_β-R_si_β)dt

定子磁链的幅值ψ_sm和相位ψ_ψ，如下：

由计算得到的定子磁链和定子电流，可以得到异步电动机电磁转矩T_e，如下：

T_e＝p_n(ψ_αi_β-ψ_βi_α)

式中，p_n为极对数；

由以上计算得到的电磁转矩、定子磁链，可以计算出电动机转子转差角速度ω_f，如下：

根据ABC坐标系下的电动机定子电压方程，可以计算出电动机定子同步角速度ω_s，如下：

则，电动机转子机械转速ω，如下：

ω＝(ω_s-ω_f)/p_n

根据电动机在ABC坐标系下的三相电压电流转换到α-β坐标系下，利用定子磁链观测的方法，得出了电动机转速；

步骤二、曲柄轴净扭矩计算

将曲柄作为等效构件，建立等效数学模型，求解减速器曲柄轴净扭矩，电动机转子与曲柄运动规律通过恒定的传动比相互确定，因此电动机匀速运行时曲柄为匀速运行，电动机变速运行时曲柄变速运行，曲柄运动规律微分方程如下：

式中M_ed为等效驱动力矩，N·m；M_ef为等效阻力矩，N·m；J_e系统转动惯量，kg·m²；θ为t时刻时曲柄所在位置的转角，rad。

电动机产生的等效驱动力矩M_ed，根据电动机的机械特性曲线得出，即

根据电动机额定参数由下式计算：

ω₀＝2πn₀/60

式中i_MB为电动机输出轴到减速箱的传动比；η_MB为电动机输出轴到减速箱的传动效率；M_M为电动机在转子角速度为的输出扭矩，N·m；λ_k为电动机最大扭矩与额定扭矩的比；M_H为额定扭矩，N·m；P_H为额定功率，kW；n₀为同步转速，min^-1；n_H为额定转速，min^-1。不难看出应用以上方法求解等效驱动力矩同样需要知道电动机转子的运动规律，即或者已知。因此本专利采用电动机定子磁链观测的方法直接计算电动机的电磁转矩(在步骤一中已有叙述)。电动机输出扭矩由皮带传递给减速箱得到的扭矩为抽油机减速箱输出净扭矩M_ed，则减速箱输出轴净扭矩M_ed的计算公式：

M_ed＝T_ei_pη_pi_jη_j

式中，T_e为电动机输出扭矩，N·m；η_p为皮带的传动效率；η_j为减速箱的传动效率；i_p为皮带的传动比；i_j减速箱的传动比。

等效阻力矩由下式计算：

式中为游梁式抽油机扭矩因数，m；PRL为抽油机悬点载荷，N；B_W为抽油机平衡配重，N；M_C为曲柄平衡力矩，N·m；τ为平衡重的滞后角，rad；η_CL为曲柄到悬点的传动效率；k₁为系数，与悬点速度相关；

等效转动惯量J_e的计算：

将由抽油机悬点到电动机转子的所有运动部件的质量和转动惯量依据动能相等的原则转化到减速器的输出轴上，则

式中，J_i为第i个部件的转动惯量，kg·m²；ω_i为第i个部件转动速度，1/s；m_i为第i个部件绕的质量，kg；v_i为第i个部件的质心运动速度，m/s。

由以上分析可知，计算等效阻力矩的方法有两种，一种方法是经过对电动机转速进行磁链观测后，可以根据曲柄运动规律微分方程和等效驱动力矩方程；另一种方法同样也是需要已知电动机运动规律后，直接利用等效力矩方程进行计算。本专利选用了直接计算的方法。根据刘华伟等人在《抽油机平衡度调整方法解析及其比对研究》的论述，这里的等效阻力矩可以认为是曲柄轴净扭矩。

根据抽油杆柱的波动方程，用F_i,j表示节点i在j时刻的抽油杆柱的载荷，用PRL表示悬点载荷，进而根据抽油机电动机的运动规律，利用运动学得出悬点的速度、加速度和位移，即可以求解悬点载荷。将悬点载荷、扭矩因数、抽油机平衡配重、曲柄平衡力矩、平衡重的滞后角以及曲柄到悬点的传动效率等参数代入曲柄净扭矩计算公式即可；

步骤三、游梁平衡的判定

如果上、下冲程中曲柄轴净扭矩的最大值的百分比大于70％，则认为平衡；否则不平衡。

由计算得到的上、下冲程中曲柄轴净扭矩的最大值进行比作为平衡度，即上、下冲程中的扭矩峰值比，如下：

式中，T_max1、T_max2为上、下冲程中的最大的扭矩值。

如果，ε大于0.7，则游梁式抽油机处于平衡状态；如果ε小于0.7，则需要调整平衡块位置，使其达到调整后平衡。

实施例一

根据现有的三种平衡判定准则和现有的平衡判定方法，以游梁式抽油机的工作原理为基础，分析了抽油机变速运行时，比如高转差率电动机驱动时，平衡判定的问题。基于此问题，利用电动机的矢量控制原理和电动机转速磁链观测方法，计算出抽油机曲柄转速，得到其变化规律，使曲柄运动方程和抽油杆柱的波动方程之间解除耦合关系，对抽油机悬点进行运动学和动力学的分析，计算了抽油机悬点的速度、加速度、位移和载荷，计算了曲柄扭矩，采用扭矩曲线进行了游梁的平衡判定。

以CYJW10-3-37HY型号的抽油机为例，对游梁式抽油机平衡度的调整判定方法进行计算验证，抽油机驱动用超高转差率电动机额定转速为740r/min，型号为YH132M-4。油井泵挂深度1000m，油管直径62mm，动液面800m，杆柱直径22mm，泵径57mm。

步骤一、计算电动机转速

采用三相交流异步电动机定子电压和电流的磁链观测模型，进行电动机转速的计算。对高转差率电动机的定子进行了三项电流电压的数据采集。为了计算方便进行了ABC坐标系到α-β坐标系的变换。

则α-β坐标系下的电压，定子电压的幅值u_s和相位如下：

定子电流的幅值i_s和相位如下：

磁链分量ψ_α和ψ_β，如下：

ψ_α＝∫(u_α-R_si_α)dt ψ_β＝∫(u_β-R_si_β)dt

定子磁链的幅值ψ_sm和相位ψ_ψ，如下：

高转差率电动机电磁转矩T_e，如下：

T_e＝p_n(ψ_αi_β-ψ_βi_α)

高转差率电动机转子转差角速度ω_f，如下：

高转差率电动机定子同步角速度ω_s，如下：

则，高转差率电动机转子机械转速ω，如下：

ω＝(ω_s-ω_f)/p_n

磁链观测的高转差率电动机转速，见图3中的电机转速所示。

步骤二、曲柄轴净扭矩计算

根据发明内容中的曲柄净扭矩的计算方法，采用了直接计算法，采用公式如下：

式中为游梁式抽油机扭矩因数，m；PRL为抽油机悬点载荷，N；B_W为抽油机平衡配重，N；M_C为曲柄平衡力矩，N·m；τ为平衡重的滞后角，rad；η_CL为曲柄到悬点的传动效率；k₁为系数，与悬点速度相关。

代入抽油机型号的尺寸的数值，直接进行计算，可求出所需要的游梁式抽油机的几何参数和悬点运动参数，包括速度、加速度和位移，计算结果见图1所示。

扭矩因数的计算，只取决于抽油机的几何尺寸和曲柄转角，计算如下：

式中：A为游梁前臂长，m；C为游梁后臂长，m；R为曲柄旋转半径，m。

等效转动惯量J_e的计算。将由抽油机悬点到电动机转子的所有运动部件的质量和转动惯量依据动能相等的原则转化到减速器的输出轴上。计算如下：

抽油机悬点载荷的计算。以下死点为位移的零点，向上为位移正方向，任意时刻悬点的位移S_i计算如下：

式中，P为连杆长度，mm；K为游梁支承中心到减速器输出轴中心的距离，mm；L为曲柄销中心到游梁支承中心之间的距离，mm。由波动方程，计算得到的悬点动载荷为：

式中，F_0,j为抽油杆柱在节点0在j时刻的载荷，即悬点载荷PRL；u(x,t)为位移函数；E_r为弹性模量；A_r为截面面积。计算结果见图2。利用以上计算的出的数据，进行计算可以得出曲柄扭矩，结果见图3。

步骤三、抽油机平衡判定

根据曲柄扭矩曲线的上、下冲程中最大的扭矩值T_max1、T_max2，则其平衡度计算如下：

所求得的上、下冲程中的曲柄净扭矩值，可知上冲程中最大扭矩值为47530N，下冲程中最大扭矩值为37240N。

则平衡度为

因平衡度ε大于0.7，说明游梁式抽油机满足平衡要求，不需再调整。