基于地震拓频处理的相控随机反演薄储层预测方法与流程

本发明涉及石油勘探、开发中储层预测
技术领域：
，特别是涉及到一种基于地震拓频处理的相控随机反演薄储层预测方法。
背景技术：
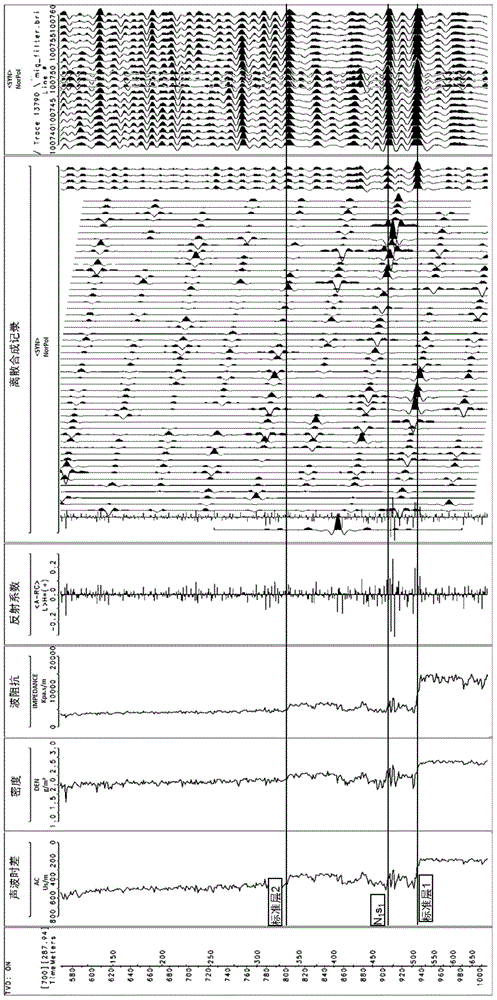
：随着石油勘探开发程度的提高，油气勘探的潜在目标越来越复杂，寻找隐蔽油气藏、薄互层油气藏已成为目前油气勘探的主要目标，这就要求不断提高相应的勘探技术水平。现有的薄储层地震预测技术有很多，包括地震拓频技术、地震属性分析技术、谱分解技术、测井约束反演技术、正演模型技术等。地震拓频技术是采用高精度的宽频带处理技术，使高频段信息进行有效增强，识别薄储层；地震属性分析技术利用的是三维地震资料横向分辨率高的优势，能够识别地震分辨率之外的储层的平面展布；谱分解技术是通过在频率域内对地震数据进行全频段扫描、成像，摆脱常规地震资料分辨率的限制，提高薄储层预测能力；测井约束反演技术的优势在于将具有高横向分辨率的地震资料和具有高纵向分辨率的测井资料有机结合，在一定程度上提高了薄储层的垂向分辨能力和横向表征精度；正演模型技术讲地质模型和地震模型有机结合，验证薄储层的地震反射特征，为利用地震资料识别薄储层提供了一定的依据。现有薄储层预测技术存在的主要问题是，测井约束反演技术、正演模型技术等识别薄储层依靠的是高纵向分辨率的测井资料的加入，没有从原始地震资料入手；而地震拓频技术、地震属性分析和谱分解等技术是对地震资料进行处理或者是运算，并没有测井资料的介入。为此我们发明了一种新的基于地震拓频处理的相控随机反演薄储层预测方法，解决了以上技术问题。技术实现要素：本发明的目的是提供一种可以提高对于薄层的预测可靠程度的基于地震拓频处理的相控随机反演薄储层预测方法。本发明的目的可通过如下技术措施来实现：基于地震拓频处理的相控随机反演薄储层预测方法，该基于地震拓频处理的相控随机反演薄储层预测方法包括：步骤1，利用地震解释数据及测井资料进行精细储层标定，明确储 层在地震剖面上的响应特征；步骤2，对目的层段地震资料开展基于拓频技术的精细目标处理，提高目的层地震资料分辨率；步骤3，根据井上储层特征分析，优选能够明确区分储层与围岩的敏感判别曲线；步骤4，对研究区的地震资料开展基于递推反演的约束稀疏脉冲反演，获得研究区的波阻抗反演数据；步骤5，以不同的研究目的层段沉积模式、沉积微相分析为前提，明确各种沉积相的储层参数空间分布规律，确定纵向及水平变程；以及步骤6，利用确定性反演数据，结合各沉积相储层参数空间分布参数，开展基于蒙特卡洛马尔科夫链算法的随机反演。本发明的目的还可通过如下技术措施来实现：在步骤1中，对声波时差曲线和密度曲线进行曲线校正，提高测井资料的可靠程度，调整不同子波进行褶积，使得合成地震记录与井旁道地震反射达到最佳匹配程度，利用地震解释数据及测井资料，建立深度域钻井资料与时间域地震的对应关系，开展精细的储层标定，明确储层在地震剖面上的响应特征。在步骤2中，受研究区目的层岩性组合的影响，研究区储层在地震资料对应地震反射弱及空白反射现象，在对研究区精细储层标定的基础上，开展地震资料提高分辨率处理：(1)选择目的层时窗；(2)时窗范围内反Q能量补偿；(3)基于测井约束的拓频处理；(4)能量均衡及去噪处理。在步骤2中，对研究区目的层段地震资料进行基于几何球面扩散补偿、地表一致性振幅补偿技术、多域面波压制技术、多域线性干扰去噪技术、预测反褶积和地表一致性串联反褶积技术的地震资料拓频处理，包括：对所述研究区目的层段地震资料采取能量补偿处理，消除非地质因素对地震信号的影响，开展叠前去噪处理及反褶积技术，提高处理精度、波组特征和成像效果，达到提高地震资料纵向分辨率的目的。在步骤3中，对井上目的层段测井数据进行交会分析，优选出区分储层与围岩的敏感判别曲线，分析得到储层敏感参数变化范围。在步骤3中，针对研究区内所用的地质、测井资料开展储层地球物理特征分析，在研究区中若波阻抗曲线能较好的区分储层与围岩即储层处于相对 高的波阻抗或者都处于相对低的阻抗，则建立波阻抗区分曲线；若波阻抗曲线不能很好的区分储层与围岩，则进行多曲线判别分析，明确区分储层与围岩的敏感判别曲线，优选出识别储层特征曲线的门槛值。在步骤4中，在精细的井震标定基础上，通过不断试验调整，明确适合研究区的确定性反演参数，获得一个高质量的确定性反演结果，用来质控随机协模拟和反演结果同时刻度随机反演结果横向预测的准确度，并对目标区的岩性展布、比例在总体上有一个正确的把握。在步骤5中，分析研究区沉积相以及物源供给情况，以不同的研究目的层段沉积模式、沉积微相分析为前提，明确各种沉积相的储层参数空间分布规律，确定纵向、水平方向变差函数，包括：分析研究区目的层段的沉积环境或者物源分布情况，利用通过地震数据提取的基本反映岩性分布情况的地震属性分块或分层进行变差函数分析，明确适合所述研究区的变差函数分析参数。在步骤6中，利用确定性地震反演作为初始模型输入及约束条件，以井的声波阻抗作为输入，结合确定的纵向、水平方向变差函数，以及直方图分析，确定出方差构造的累计条件分布概率函数，沿着协方差函数场中某一网格化的随机路径有序的模拟，利用蒙特卡洛马尔科夫链算法获得每一个网格节点处的随机函数值，建立波阻抗与优选出的判别曲线之间的线性关系，进而模拟出高分辨率的储层敏感参数的数据体，获得区分储层与围岩的某储层参数反演剖面，依据优选出的储层与围岩判别曲线的门槛值开展有利储层的预测描述。在步骤6中，在一个给定的空间数据集上，设条件数据为{Z(xa)，a(n)}，Z(x)为未采样点即待模拟点值；首先，对变量场的分布特征进行分级，目的是将累计条件分布概率函数值限制于所分类别之中，设Z0为级别中的门槛值，定义x点处的二值指示变量为：I(x,Z0)=0Z(x)>Z01Z(x)≤Z0---(1)]]>可以证明，其条件期望值为E{I(x,Z0)|Z(xa),a∈(n)}＝P{Z(x)≤Z0|Z(xa),a∈(n)}(2)其中，P{Z(x)≤Z0|Z(xa),a∈(n)}是指示变量的条件概率分布值，式(2)表明，通过指示变量条件期望值的估算，可以得到其相应的条件概率分布值，条件期望值通过克立格法对条件数据进行指示转换来估算，亦即利用条件数据点Z(xa)，由指示克立格可得到期望值的最优无偏线性估计，期望估计值即为累计条件分布概率函数的估计值，即有F*{Z(x)≤Z0|Z(xa),a∈(n)}=Σa=1nλa(x,Z0)i(xa,Z0)---(3)]]>在这里F*为累计条件分布概率函数估计值，i(xa,Z0)为以Z0为门槛的样点值Z(xa)的指示变换，λa(x,Z0)为克里格权系数克里格权系数则可以通过知识克里格方程求得，即有Σb=1nλb(x,Z0)C1(xb-xa,Z0)+μ(x,Z0)=C1(x-xa,Z0)(a=1,2,...,n)Σb=1nλb(x,Z0)=1---(4)]]>(4)式中λb(x,Z0)为克里格权系数，C1(xb-xa,Z0)和C1(x-xa,Z0)为指示协方差函数，μ为拉格朗日常数，通过以上求取累计条件分布概率函数估计值，便可以利用蒙特卡洛马尔科夫链算法模拟每一网格节点的随机函数值，在位置x处抽取一个均匀随机数P(m)∈[0,1]，然后转换为累计条件分布概率函数估计值的分位数值，该分位数即为位置x的模拟值，即有F*(-1){x；Zm(x)|(n)}＝P(m)(5)Zm(x)＝F*(-1){x；P(m)|(n)}(5)式中Zm(x)为位置x的模拟值，F*(-1)为逆累计条件分布概率函数估计值或P(m)∈[0,1]的分位数函数，在此基础上，对指示数据集采用模拟值进行更新，这样，一个网格点的模拟完成，再对另外的位置沿着随机路径继续使用指示模拟。本发明中的基于地震拓频处理的相控随机反演薄储层预测方法，在地震资料分辨率较低的问题上通过拓频处理技术提高原始地震资料的分辨率；在利用随机反演技术开展储层预测过程中，针对不同沉积相(包括沉积微相)砂体的厚度及平面分布形态，建立不同沉积相与反演相关参数之间最优配置关系，设置了对应优化的变程等反演参数，使得反演效果达到最佳，从而提高对于薄层的预测可靠程度。附图说明图1为本发明的基于地震拓频处理的相控随机反演薄储层预测方法的一具体实施例的流程图；图2为本发明的一具体实施例中某井合成地震记录层位标定流程示意图；图3为本发明的一具体实施例中地震资料拓频解释性处理前的示意图；图4为本发明的一具体实施例中地震资料拓频解释性处理后的示意图；图5为本发明的一具体实施例中不同测井资料区分储层、围岩对比显示图；图6为本发明的一具体实施例中随机反演过程中变程变差函数相关参数设置示意图；图7为本发明的一具体实施例中某地区well1-well2连井随机反演剖面的示意图。具体实施方式下面结合实例和附图对本发明的一种基于地震拓频处理的相控随机反演薄储层预测方法予以进一步说明，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。如图1所示，图1为本发明的基于地震拓频处理的相控随机反演薄储层预测方法的流程图。在步骤101，利用地震解释数据及测井资料进行精细储层标定，明确储-震对应关系。对某一研究区的声波时差曲线和密度曲线标定，建立深度域与时间域的对应关系，开展精细的储层标定，明确储层在地震剖面上的响应特征。对声波时差曲线和密度曲线进行校正，提高资料的可靠程度。调整不同子波进行褶积，使得合成地震记录与井旁道地震反射达到最佳匹配程度，利用地震解释数据及测井资料，建立深度域钻井资料与时间域地震的对应关系，开展精细的储层标定，明确储层在地震剖面上的响应特征。图2为本发明应用实例合成地震记录层位标定流程示意图，图中包括了声波时差测井曲线、密度曲线、波阻抗曲线、反射系数序列、地震子波、离散合成记录、合成记录及井旁地震道，通过精细的标定过程，可以明确目的层段储层顶底在地震上的对应关系。流程进入到步骤102。在步骤102，对目的层段地震资料开展基于拓频技术的精细目标处理，提高目的层地震资料分辨率。受所述研究区目的层岩性组合的影响，研究区储层在地震资料对应地震反射弱及空白反射现象，在对所述研究区精细储层标定的基础上，开展地震资料提高分辨率拓频处理：(1)选择目的层时窗；(2)时窗范围内反Q能量补偿；(3)基于测井约束的拓频处理；(4)能量均衡及去噪处理。在一实施例中，对所述研究区目的层段地震资料进行基于几何球面扩散补偿、地表一致性振幅补偿技术、多域面波压制技术、多域线性干扰去噪技术、预测反褶积和地表一致性串联反褶积技术的地震资料拓频处理，包括：对所述研究区目的层段地震资料采取能量补偿处理，消除非地质因素对地震信号的影响。开展叠前去噪处理及反褶积技术，提高处理精度、波组特征和成像效果，达到提高地震资料纵向分辨率的目的。图3和图4为拓频解释性处理前后对比图，图3为原始地震剖面，由于地震分辨率较低以及储层位于强反射附近的原因，储层在原始地震剖面中没有 形成反射。图4为拓频提高分辨率处理后地震剖面，由于分辨率的提高，砂岩储层位置出现地震反射。流程进入到步骤103。在步骤103，对井上测井数据进行交会分析，优选出测井数据交会图上储层与围岩的敏感判别曲线，分析得到储层的参数范围。针对研究区内所用的地质、测井资料开展储层地球物理特征分析，在所述研究区中如果储层与围岩的相对关系在波阻抗曲线上是区分的即储层处于相对高的波阻抗或者都处于相对低的阻抗，则建立波阻抗区分曲线，如果阻抗不能很好的区分储层与围岩，则进行多曲线判别分析，明确区分储层与围岩的敏感判别曲线，优选出识别储层特征曲线的门槛值。图5为同测井资料区分储层、围岩对比显示图，图中包括了某井的岩性柱状剖面、自然电位曲线、电阻率曲线、自然伽马、波阻抗、声波时差、密度曲线，对比发现，自然电位对砂岩段储层指示敏感。电阻率曲线虽然对目标层砂岩有一定的指示作用，但并不代表所述研究区储层段的普遍规律，因此，选定自然电位曲线作为所述研究区目的层段砂体展布规律预测的敏感曲线。流程进入到步骤104。在步骤104，对研究区的地震资料开展基于递推反演的约束稀疏脉冲反演，获得所述研究区的波阻抗反演数据。在精细的井震标定基础上，通过不断试验调整，明确适合研究区的确定性反演参数，获得一个高质量的确定性反演结果，用来质控随机协模拟和反演结果同时刻度随机反演结果横向预测的准确度，并对目标区的岩性展布、比例在总体上有一个正确的把握。在一实施例中，通过步骤101中精细的井震标定基础上，将深度域的资料精确的标定到时间域的地震剖面上，通过不断试验调整，最终明确适合研究区的确定性反演参数，获得一个高质量的确定性反演结果，对目标区的岩性展布、比例在总体上有一个正确的把握。流程进入到步骤105。在步骤105，以不同的研究目的层段沉积模式、沉积微相分析为前提，明确各种沉积相的储层参数空间分布规律，确定纵向、水平方向变差函数。分析所述研究区沉积相以及物源供给情况，以不同的研究目的层段沉积模 式、沉积微相分析为前提，明确各种沉积相的储层参数空间分布规律，确定纵向、水平方向变差函数，包括：分析研究区目的层段的沉积环境或者物源分布情况，利用通过地震数据提取的基本反映岩性分布情况的地震属性分块或分层进行变差函数分析，明确适合所述研究区的变差函数分析参数。图6为随机反演过程中变差函数分析相关参数设置示意图，图中重点参数包括了变程、基台值、块金常数，图中重要的一个参数为变程，变程的大小不仅能反映储层参数在某一方向上变化的大小，而且还能从总体上反映出砂体在某个方向的平均尺度，从而可利用变程来预测砂体在某个方向上的延伸尺度，达到实现预测砂体规模的目的。通过变差函数的拟合分析，可以获得在纵向上的变程，然后，根据不同的沉积相，分析不同沉积模式下砂体的分布规模，最终分沉积模式的水平变程参数。流程进入到步骤106。在步骤106，利用确定性地震反演作为初始模型输入及约束条件，结合各沉积相储层参数空间分布规律，开展基于蒙特卡洛马尔科夫链算法的随机反演，获得区分储层与围岩的某储层参数反演剖面。依据优选出的储层与围岩判别曲线的门槛值开展有利储层的预测描述，包括：利用确定性地震反演作为初始模型输入及约束条件，以井的声波阻抗作为输入，建立波阻抗与优选出的判别曲线之间的线性关系，进而模拟出高分辨率的储层敏感参数的数据体。在一实施例中，利用确定性地震反演作为初始模型输入及约束条件，结合105中确定的纵向变程和水平方向的变程参数，以及直方图分析，确定出方差构造的累计条件分布概率函数，沿着协方差函数场中某一网格化的随机路径有序的模拟，利用蒙特卡洛马尔科夫链算法获得每一个网格节点处的随机函数值，具体步骤包括：在一个给定的空间数据集上，设条件数据为{Z(xa)，a(n)}，Z(x)为未采样点(待模拟点)值。首先，对变量场的分布特征进行分级(类)，目的是将累计条件分布概率函数值限制于所分类别之中。设Z0为级别中的门槛值，定义x点处的二值指示变量为：I(x,Z0)=0Z(x)>Z01Z(x)≤Z0---(1)]]>可以证明，其条件期望值为E{I(x,Z0)|Z(xa),a∈(n)}＝P{Z(x)≤Z0|Z(xa),a∈(n)}(2)其中，P{Z(x)≤Z0|Z(xa),a∈(n)}是指示变量的条件概率分布值。式(2)表明，通过指示变量条件期望值的估算，可以得到其相应的条件概率分布值。条件期望值通过克立格法对条件数据进行指示转换(指示克立格)来估算，亦即利用条件数据点Z(xa)，由指示克立格可得到期望值的最优无偏线性估计。期望估计值即为累计条件分布概率函数的估计值，即有F*{Z(x)≤Z0|Z(xa),a∈(n)}=Σa=1nλa(x,Z0)i(xa,Z0)---(3)]]>在这里F*为累计条件分布概率函数估计值，i(xa,Z0)为以Z0为门槛的样点值Z(xa)的指示变换，λa(x,Z0)为克里格权系数克里格权系数则可以通过知识克里格方程求得，即有Σb=1nλb(x,Z0)C1(xb-xa,Z0)+μ(x,Z0)=C1(x-xa,Z0)(a=1,2,...,n)Σb=1nλb(x,Z0)=1---(4)]]>(4)式中λb(x,Z0)为克里格权系数，C1(xb-xa,Z0)和C1(x-xa,Z0)为指示协方差函数，μ为拉格朗日常数。通过以上求取累计条件分布概率函数估计值，便可以利用蒙特卡洛马尔科夫链算法模拟每一网格节点的随机函数值。在位置x处抽取一个均匀随机数P(m)∈[0,1]，然后转换为累计条件分布概率函数估计值的分位数值，该分位数即为位置x的模拟值，即有F*(-1){x；Zm(x)|(n)}＝P(m)(5)Zm(x)＝F*(-1){x；P(m)|(n)}(5)式中Zm(x)为位置x的模拟值，F*(-1)为逆累计条件分布概率函数估计值或P(m)∈[0,1]的分位数函数在此基础上，对指示数据集采用模拟值进行更新，这样，一个网格点的模拟完成，可以对另外的位置沿着随机路径继续使用指示模拟。图7是本发明实施例所述研究区well1-well2连井随机反演剖面，从反演剖面上可以看出，能较好的刻画出目的层段砂体的横向展布规律及砂体在井间的连续性。本发明通过精细的储层标定，明确储层在地震剖面上的响应特征，针对所述研究区地震资料的弱反射或者空白反射现象，采用静校正、反Q能量补偿、去噪处理等一系列处理技术，提高地震资料的纵向分辨率，在此基础上，分沉积相确定随机反演的反演参数，采用了确定性反演与随机反演相结合的方法，有效提高了反演的精度。以上所述的具体实施方式，对本发明的目的、技术方案和有益效果进行了进一步的说明，所应理解的是，以上所述仅为本发明的具体实施方式而已，并不用于限定本发明的保护范围，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。当前第1页1 2 3