机械零部件的疲劳寿命评估方法与流程

本发明涉及机械零部件的疲劳寿命评估方法。
背景技术：
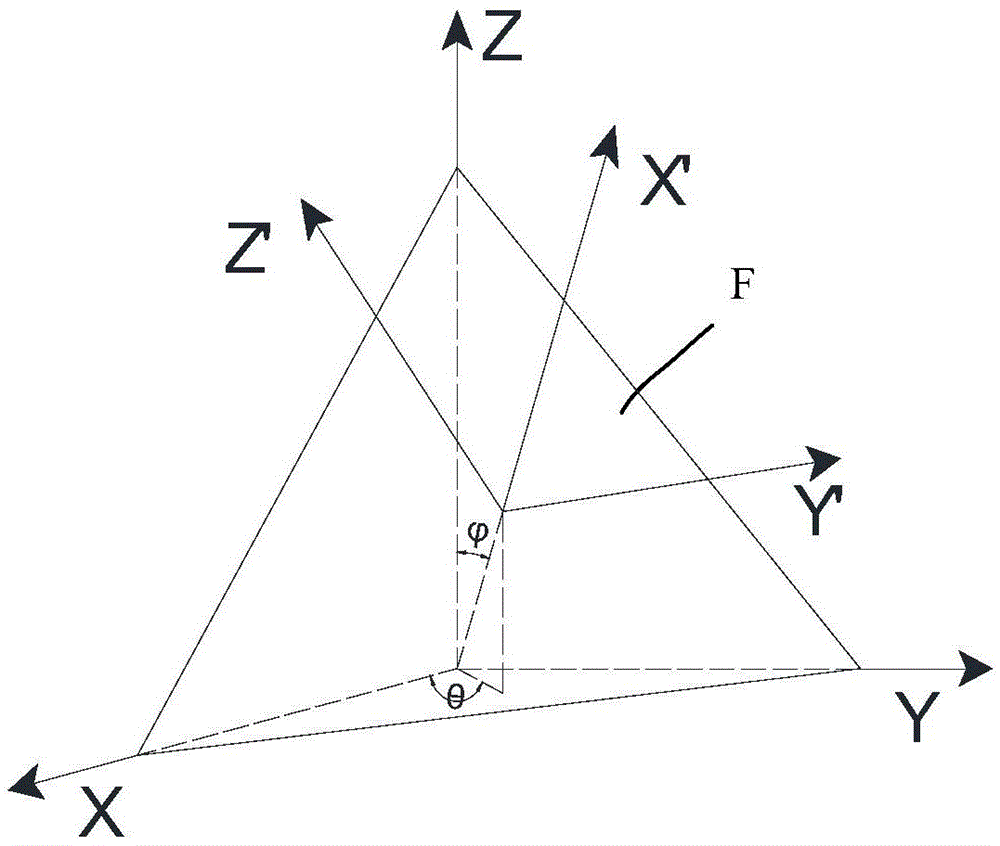
：航空发动机热端部件如涡轮叶片、榫槽等部位往往在高温、高应力的苛刻工作条件下服役，而由于结构形式、载荷条件复杂性，其应力应变状态往往处于三维变幅多轴状态，对其进行高温、三维多轴疲劳寿命评估就成为这些部件设计阶段的一项重要工作。这些部件对于可靠性、轻量化设计具有重大需求.高温部件工作温度往往也变化剧烈。目前工程上对于评估零部件在三维应力应变、变幅载荷、变温高温工作条件下机械零部件的疲劳寿命具有较大的困难。技术实现要素：本发明的目的在于提供一种机械零部件的疲劳寿命评估方法。为实现所述目的的机械零部件的疲劳寿命评估方法，其包括获取载荷历程数据；对载荷历程数据的载荷历程反复计数；基于临界面法确定临界面及其损伤参量；对于每一个所述载荷历程反复，若其最高温度T低于材料的蠕变开始发生温度，则仅评估疲劳损伤Df1，若T达到蠕变开始发生温度，则评估疲劳损伤Df2并且评估蠕变损伤Dc；根据公式D＝∑Df1+∑Df2+∑Dc评估总损伤；由总损伤评估疲劳寿命。所述的疲劳寿命评估方法的较佳实施例中，对于每一个所述载荷历程反复，基于其最高温度T来评估疲劳损伤Df1以及蠕变损伤Dc，并基于不高于T的温度来评估疲劳损伤Df2。所述的疲劳寿命评估方法的较佳实施例中，评估疲劳损伤Df1或Df2是依据所述T对应的应变-寿命曲线获得，或者具有从低到高的不低于常温的T1，T2……Tn共n个温度对应n条应变-寿命曲线获得，即其中，Df为Df1或Df2，DfTi是对应温度Ti的疲劳损伤，1<i<n，Ti为第i条应变-寿命曲线对应的温度，Tm为材料的熔化温度，i和n为整数。所述的疲劳寿命评估方法的较佳实施例中，所述载荷历程数据包括时间t、以及对应该时间t的温度、各方向正应力σ和正应变ε、各方向剪应力τ和剪应变γ，其中三维应力矩阵和应变矩阵如下：应变矩阵：ϵxγxyγxzγyxϵyγyzγzxγzyϵz,]]>其中γxy＝γyx,γxz＝γzx,γyz＝γzy应变矩阵独立分量为[εxεyεzγxyγyzγzx]应力矩阵：σxτxyτxzτyxσyτyzτzxτzyσz,]]>其中τxy＝τyx,τxz＝τzx,τyz＝τzy应力独立分量为：[σxσyσzτxyτyzτzx]其中：εx,εy,εz为X-Y-Z直角坐标系下的正应变；γxy,γyz,γzx,γyx,γzy,γxz为X-Y-Z坐标系下的剪应变；σx,σy,σz为X-Y-Z坐标系下的正应力；τxy,τyz,τzx,τyx,τzy,τxz为X-Y-Z坐标系下的剪应力。所述的疲劳寿命评估方法的较佳实施例中，确定临界面的方法首先对各点应变矩阵和应力矩阵进行坐标转换，由坐标系X-Y-Z下的应变、应力分量得到坐标系X’-Y’-Z’下的应变、应力分量，然后依据临界面的设定条件获得临界面的位向角和临界面上的损伤参量，其中应变转换矩阵为：ϵx′ϵy′ϵz′γx′y′γx′z′γy′z′=a112a122a132a11a12a11a13a13a12a212a222a232a21a22a21a23a23a22a312a322a332a31a32a31a33a33a322a11a212a12a222a13a23(a11a22+a12a21)(a13a21+a11a23)(a12a23+a13a22)2a11a312a12a322a13a33(a11a32+a12a31)(a13a31+a11a33)(a13a32+a12a33)2a21a312a22a322a23a33(a21a32+a22a31)(a23a31+a21a33)(a22a33+a23a32)ϵxϵyϵzγxyγxzγyz]]>应力转换矩阵为：σx′σy′σz′τx′y′τx′z′τy′z′=a112a122a1322a11a122a11a132a13a12a212a222a2322a21a222a21a232a23a22a312a322a3322a31a322a31a332a33a32a11a21a12a22a13a23(a11a22+a12a21)(a13a21+a11a23)(a12a23+a13a22)a11a31a12a32a13a33(a11a32+a12a31)(a13a31+a11a33)(a13a32+a12a33)a21a31a22a32a23a33(a21a32+a22a31)(a23a31+a21a33)(a22a33+a23a32)σxσyσzτxyτxzτyz]]>其中转换矩阵的系数为：a21＝-sinθa22＝cosθa23＝0θ和为确定坐标系X’-Y’-Z’相对于坐标系X-Y-Z位置关系的两个夹角。所述的疲劳寿命评估方法的较佳实施例中，蠕变损伤为Dc=ttc]]>其中t为一个反复的周期，tc为持久断裂时间，tc依据持久热强参数综合方程求解，持久应力采用下式计算：σc=σeq|max+σeq|min2]]>其中σeq|max为一个反复的最大等效应力；σeq|min为一个反复的最小等效应力；σc为一个反复的持久应力。所述的疲劳寿命评估方法的较佳实施例中，疲劳损伤Df1或Df2是基于统一型多轴疲劳寿命预测模型评估，所述损伤参量包括最大剪切应力变幅和最大正应力变幅。所述的疲劳寿命评估方法的较佳实施例中，获取载荷历程数据还包括载荷历程整理，依次求出每一个时刻点的等效应变，载荷历程数据在最大等效应变点处断开，将该点之前数据作为最后一个时刻点之后载荷历程数据。所述的疲劳寿命评估方法的较佳实施例中，基于多轴循环计数方法(如Wang-Brown等效相对应变的多轴计数方法)，对整理后的多轴载荷历程进行反复计数。所述的疲劳寿命评估方法的较佳实施例中，所述机械零部件的疲劳为三维应力应变状态下的高温且变幅多轴且低周疲劳，所述高温是所述工况的最高温度大于所述机械零部件材料的蠕变开始温度，所述变幅多轴是多向应力或应变变化，所述低周是疲劳破坏发生时载荷不高于106个循环。工程上处理蠕变疲劳的方法常见有时间寿命分数法、基于连续损伤力学(CDM)的方法、应变范围区分法等等。与其不同的是，前述方法将蠕变损伤和疲劳损伤分别考虑，因此前述方法提高了计算的准确性和合理性。附图说明本发明的上述的以及其他的特征、性质和优势将通过下面结合附图和实施例的描述而变得更加明显，其中：图1为本发明一实施例中机械零部件的疲劳寿命评估方法的流程图；图2为本发明一实施例中示意临界面获取方法的示意图。具体实施方式下面结合具体实施例和附图对本发明作进一步说明，在以下的描述中阐述了更多的细节以便于充分理解本发明，但是本发明显然能够以多种不同于此描述的其它方式来实施，本领域技术人员可以在不违背本发明内涵的情况下根据实际应用情况作类似推广、演绎，因此不应以此具体实施例的内容限制本发明的保护范围。如图1所示，机械零部件的疲劳寿命评估方法包括获取载荷历程数据，获取载荷历程数据可以是通过传感器测量机械零部件的疲劳部位的载荷大小，然后将测量数据输入到计算装置中，机械零部件的疲劳部位的位置可以是通过经验获得，或者是通过实验获得，或者通过计算获得。载荷历程数据可以包括时间t、以及对应该时间t的温度、各方向正应力σ和正应变ε、各方向剪应力τ和剪应变γ，其中三维应力矩阵和应变矩阵如下：应变矩阵：ϵxγxyγxzγyxϵyγyzγzxγzyϵz,]]>其中γxy＝γyx,γxz＝γzx,γyz＝γzy应变矩阵独立分量为[εxεyεzγxyγyzγzx]应力矩阵：σxτxyτxzτyxσyτyzτzxτzyσz,]]>其中τxy＝τyx,τxz＝τzx,τyz＝τzy应力独立分量为：[σxσyσzτxyτyzτzx]其中：εx,εy,εz为X-Y-Z直角坐标系下的正应变；γxy,γyz,γzx,γyx,γzy,γxz为X-Y-Z坐标系下的剪应变；σx,σy,σz为X-Y-Z坐标系下的正应力；τxy,τyz,τzx,τyx,τzy,τxz为X-Y-Z坐标系下的剪应力。在非三维应力应变状态下的机械零部件，可以将前述z向的分量设置为0。获得的载荷历程通常对应机械零部件的一个载荷循环的数据。还可以对获得的载荷历程数据进行整理，例如依次求出每一个时刻点的等效应变，载荷历程数据在最大等效应变点处断开，将该点之前数据作为最后一个时刻点之后载荷历程数据。继续参照图1，依据本发明的疲劳寿命评估方法还包括对载荷历程数据的载荷历程反复(或者循环)计数。对反复的计数包括但不限于是基于Wang-Brown等效相对应变的多轴计数方法，对整理后的多轴载荷历程进行反复计数。继续参照图1，依据本发明的疲劳寿命评估方法还包括基于临界面法确定临界面及其损伤参量。在本发明的一实施例中，临界面的设定条件是最大剪切应变幅△γmax所在的面，损伤参量同样选取△γmax。在本发明的其他实施例中，临界面可以通过其他设定条件而确定。临界面上的损伤参量包括但不限于正应力、剪切应力、正应变、剪切应变。参照图1和图2，确定临界面的方法首先对各点应变矩阵和应力矩阵进行坐标转换，由坐标系X-Y-Z下的应变、应力分量得到坐标系X’-Y’-Z’下的应变、应力分量，然后依据临界面的设定条件获得临界面的位向角和临界面上的损伤参量，其中应变转换矩阵为：ϵx′ϵy′ϵz′γx′y′γx′z′γy′z′=a112a122a132a11a12a11a13a13a12a212a222a232a21a22a21a23a23a22a312a322a332a31a32a31a33a33a322a11a212a12a222a13a23(a11a22+a12a21)(a13a21+a11a23)(a12a23+a13a22)2a11a312a12a322a13a33(a11a32+a12a31)(a13a31+a11a33)(a13a32+a12a33)2a21a312a22a322a23a33(a21a32+a22a31)(a23a31+a21a33)(a22a33+a23a32)ϵxϵyϵzγxyγxzγyz]]>应力转换矩阵为：σx′σy′σz′τx′y′τx′z′τy′z′=a112a122a1322a11a122a11a132a13a12a212a222a2322a21a222a21a232a23a22a312a322a3322a31a322a31a332a33a32a11a21a12a22a13a23(a11a22+a12a21)(a13a21+a11a23)(a12a23+a13a22)a11a31a12a32a13a33(a11a32+a12a31)(a13a31+a11a33)(a13a32+a12a33)a21a31a22a32a23a33(a21a32+a22a31)(a23a31+a21a33)(a22a33+a23a32)σxσyσzτxyτxzτyz]]>其中转换矩阵的系数为：a21＝-sinθa22＝cosθa23＝0θ和为确定坐标系X’-Y’-Z’相对于坐标系X-Y-Z位置关系的两个夹角。如图2所示，设定的临界面F以与坐标系X-Y-Z分别相交的三角形来表示，坐标系X’-Y’-Z’中的轴X’为临界面F的法向，并与坐标系X-Y-Z的原点相交，夹角θ为轴X’在XY平面内的投影与轴X的夹角，夹角为轴X’与轴Z的夹角，通过夹角θ、可以确定一个坐标系X’-Y’-Z’相对于坐标系X-Y-Z位置关系，这个位置关系足以用来最终确定临界面的位置。在临界面的设定条件是最大剪切应变幅△γmax所在的面的条件下，将θ、分别以5°的变幅在360度范围内变化，然后将最大剪切应变幅△γmax对应的θ、用来确定临界面的位置。另外，根据前述转换矩阵，可以计算相应的损伤参量。继续参照图1，依据本发明的疲劳寿命评估方法还包括获得每个反复的温度，对于每一个所述载荷历程反复，若其最高温度T低于材料的蠕变开始发生温度，则仅评估疲劳损伤Df1，若T达到蠕变开始发生温度，则评估疲劳损伤Df2并且评 估蠕变损伤Dc。在本发明的一实施例中，每个时间点的温度都可能是不同的，在一个反复中取其最高温度作为计算温度T。对于金属材料，一般认为蠕变发生与否和金属的熔点温度Tm有关，一般可根据计算温度十分大于Tm的一半进行判断。因此如果T低于材料熔化温度Tm的一半，则按照高温疲劳计算。若T高于熔化温度Tm的一半，则按照蠕变疲劳计算。但界限不一定是要Tm的一半，对于合金，蠕变发生开始温度一般在(0.4-0.6)Tm。评估疲劳损伤Df1或Df2是依据温度T对应的已知应变-寿命曲线获得。若没有对应的已知应变-寿命曲线，可以从具有从低到高的不低于常温的T1，T2……Tn共n个温度对应n条应变-寿命曲线获得，即其中，Df为Df1或Df2，DfTi是对应温度Ti的疲劳损伤，1<i<n，Ti为第i条应变-寿命曲线对应的温度，Tm为材料的熔化温度，i和n为整数。蠕变疲劳产生疲劳损伤Df2可以采用最低温度对应的应变-寿命曲线获得。在本发明一实施例中，疲劳损伤Df1或Df2是基于统一型多轴疲劳寿命预测模型评估。统一型多轴疲劳寿命预测模型的计算公式如下：ϵn*2+13(Δγmax2)2=σ′fE(2Nf)b+ϵ′f(2Nf)c]]>其中△γmax分别为临界面的正应变范围以及剪切应变范围，σ'f，b，ε'f，c为机械零部件的材料低周疲劳参数。在本发明的一是实施例中，蠕变损伤为Dc=ttc]]>其中t为一个反复的周期，tc为持久断裂时间，tc依据持久热强参数综合方程求解，持久应力采用下式计算：σc=σeq|max+σeq|min2]]>其中σeq|max为一个反复的最大等效应力；σeq|min为一个反复的最小等效应力；σc为一个反复的持久应力。持久热强参数综合方程可以是拉森-米勒(Larson-Miller)持久热强参数综合方程或者曼森-索克普(Manson-Succop)持久热强参数综合方程。材料持久热强参数综合方程(L-M)形式为：lgσ＝5.891306-11.71323P+17.52412P2-17.28321P3其中P＝T(lgt+25.32)/105,T＝(9θ/5+32)+460，θ为摄氏温度可以代入前述计算温度，方程中的σ可以代入前述σc，这样可以求得方程中的t，即得到前述持久断裂时间tc。本发明的评估方法然后根据公式D＝∑Df1+∑Df2+∑Dc评估总损伤。最后由总损伤评估疲劳寿命。疲劳寿命N与总损伤的关联关系可以是N＝1/D，也可以是其他方式，例如D＝1/N+1/N2。值得一提的是，本发明的疲劳寿命评估方法不仅适合于金属也适合于塑料，尤其适合于机械零部件的疲劳为三维应力应变状态下的高温且变幅多轴且低周疲劳的情况，所述高温是所述工况的最高温度大于所述机械零部件材料的蠕变开始温 度，所述变幅多轴是多向应力或应变变化，所述低周是疲劳破坏发生时载荷不高于106个循环。下面通过具体的载荷数据历程进一步说明前述具体实施方式。后述的示例中临界面是基于最大剪切应变幅的临界面，疲劳损伤模型采用了统一型多轴疲劳寿命预测模型，持久损伤计算采用了拉森-米勒(Larson-Miller)持久热强参数综合方程，损伤累积采用Miner定理，即线性损伤累计方法。示例中最终求取的结果D为总损伤，N为寿命，即为评估结果。示例采用的材料低周疲劳参数如下表1，持久热强参数综合方程如表2，材料熔点为1290℃。表格1材料低周疲劳参数温度/℃σfEεfbc36016982100000.949-0.07-0.8455015461982000.412-0.07-0.7365014761820000.108-0.09-0.58表格2材料持久热强参数综合方程参数ba0a1a2a3熔点25.1251.5660025.671844.353919-23.602521290材料持久热强参数综合方程(L-M)形式为：lgσ＝5.891306-11.71323P+17.52412P2-17.28321P3其中P＝T(lgt+25.32)/105,T＝(9θ/5+32)+460，θ为摄氏温度统一型多轴疲劳寿命预测模型为：ϵn*2+13(Δγmax2)2=σ′fE(2Nf)b+ϵ′f(2Nf)c]]>其中：和△γmax为临界面法求出的多轴疲劳损伤参量。获得的历程数据如下表3(其中应变为单位为％，应力单位为MPa，时间单位为ms)：表格3输入数据步骤1)：读取载荷历程数据。载荷历程数据中包含每一时刻点的时间t、温度T、各方向正应力σ和正应变ε、各方向剪应力τ和剪应变γ等共14项数据，如上表格。步骤2)：载荷历程整理。依次求出每一个时刻点的等效应变，载荷历程数据在最大等效应变点处断开，该点之前数据平移到最后。示例中的最大等效应变点为第11行，平移并调整之后的历程如下表：表格4调整之后的载荷历程数据步骤3)：多轴载荷历程反复计数。基于Wang-Brown等效相对应变的多轴计数方法，对整理后的多轴载荷历程进行反复计数。统计出该历程包含两个反复：第1-18行和第18-35行，用时间表示为11000ms-28000ms和28000ms-45000ms。步骤4)：基于临界面法确定三维应力/应变状态下的临界面及其损伤参量。根据所采用的统一型多轴疲劳模型，以最大剪应变所在面为临界面，临界面上损伤参量为临界面件应变范围Δγ和临界面剪应变折返点间正应变范围Δε即如果每次新坐标系对θ或旋转的角度为5°(变幅大小)，以最大剪应变幅所在的变为临界面，可以求出，第一个反复的临界面位向角为θ＝340°，第二个反复的临界面位向角为θ＝340°，求解结果如下：表格5临界面法求解结果步骤5)：通过确定每个反复的计算温度，确定损伤计算的方法。材料熔点为1290℃，熔点的一半为645℃；可以求出第一个反复的计算温度为500℃，低于645℃，按照高温疲劳损伤计算方法计算；第二个反复计算温度为650℃，高于645℃，按照蠕变-疲劳损伤求解方法计算。步骤6)：计算多轴疲劳损伤。选择统一型多轴疲劳寿命预测模型ϵn*2+13(Δγmax2)2=σ′fE(2Nf)b+ϵ′f(2Nf)c]]>将步骤4)求出的临界面求解参量和材料参数代入，即可求解该反复应计入的疲劳损伤。对于变温的处理方法：第一个反复的计算温度为500℃，按照高温疲劳求解疲劳损伤，疲劳损伤按照360℃和550℃下的低周疲劳应变-寿命曲线插值计算疲劳损伤，不计持久损伤；按照统一型多轴疲劳寿命预测模型，360℃条件疲劳损伤为0.0003493,550 ℃条件下疲劳损伤为0.0003888，则插值计算500℃条件下疲劳损伤为0.0003784；第二个反复的计算温度为650℃，超过了材料熔点的一半，采用多轴蠕变-疲劳损伤计算方法求疲劳损伤。采用360℃(已有的最低温度)条件下材料疲劳参数计算疲劳损伤，依据统一型多轴疲劳寿命预测模型可以求出疲劳损伤为0.0003446。步骤7)：求持久蠕变损伤。第二个反复的计算温度为650℃，超过了材料熔点的一半，需要计算持久蠕变损伤。该反复内最高等效应力为653MPa，最低等效应力为17Mpa，则持久应力为0.5*(653+17)＝335MPa，持久断裂时间为3761h，该反复的持续时间为45000-28000＝17000ms，则持久损伤为17000/1000/3600/3761＝1.2e-6。步骤8)：损伤累积。本例采用线性损伤累计方法。总损伤为：D＝0.0003784+(0.0003446+0.0000012)＝0.0007242寿命为：N＝1/D＝1381块，即经过1381个示例载荷快，该评估点发生蠕变-疲劳破坏。经过以上八个步骤，即完成了对该高温条件下三维应力应变状态的蠕变-疲劳损伤评估。工程上处理蠕变疲劳的方法常见有时间寿命分数法、基于连续损伤力学(CDM)的方法、应变范围区分法等等。前述实施方式时间寿命分数法将蠕变损伤和疲劳损伤分算。温度升高会造成材料性能下降，而在变温作用下对于疲劳损伤求解，采用单一温度下的应变寿命曲线就会不准确，而又不可能具有每个温度下的应变寿命曲线，前述实施例提出了变温作用下的疲劳损伤插值计算方法，提高了计算的准确性和合理性。材料发生多轴蠕变疲劳破坏，由于应力是多轴的且大小是变化，不能简单地通过采用某一个应力分量来表征持久应力来求出蠕变损伤，前述实施例提出了在多轴蠕变疲劳损伤计算中一个反复的持久应力计算方法，为蠕变损伤确定提供了依据。前述实施例尤其适合于评估处于高温环境、三维应力应变状态工作条件的 热端部件低周多轴蠕变-疲劳损伤评估和寿命预测，本发明人已经过试验验证，该方法在评估热端部件高温蠕变-疲劳寿命上具有较高的精度。本发明虽然以较佳实施例公开如上，但其并不是用来限定本发明，任何本领域技术人员在不脱离本发明的精神和范围内，都可以做出可能的变动和修改。因此，凡是未脱离本发明技术方案的内容，依据本发明的技术实质对以上实施例所作的任何修改、等同变化及修饰，均落入本发明权利要求所界定的保护范围之内。当前第1页1 2 3