一种基于谱反演的砂体厚度预测方法及系统与流程

本发明属于石油勘探地震储层预测技术领域，具体地说，尤其涉及一种基于谱反演的砂体厚度预测方法及系统。

背景技术：

随着油气藏勘探开发的不断深入，开发目标不再是以厚储层为主的构造油气藏，而是更多为储层厚度较薄(单砂体厚度多小于10米)的复杂油气藏。

厚度大于1/4波长的储层存在调谐效应，结合测井资料阻抗反演和拟声波反演可以满足储层识别需求。受目前地震分辨率影响，当地震子波主频为30hz左右时，很难分辨厚度小于1/4波长(20米以下)薄砂体的顶、底地震反射。而现今勘探开发层系的河道砂体厚度往往小于1/4波长，且沉积相横向变化快，河道薄砂体的识别与预测问题日益突出。

因此，需要一种能够提高地震资料分辨率、预测厚度小于1/4波长薄层砂体的方法。

技术实现要素：

为解决以上问题，本发明提供了一种基于谱反演的砂体厚度预测方法及系统，用于提高厚度小于1/4波长薄层砂体厚度的预测精度。

根据本发明的一个方面，提供了基于谱反演的砂体厚度预测方法，包括：

从原始地震数据中获取地震子波和地层反射系数；

建立目标函数，并根据所述目标函数、所述地震子波、奇偶分解后的地层反射系数进行谱反演，以获取偶分量反射系数序列；

根据所述地震子波、所述偶分量反射系数序列和所述目标函数合成新地震数据；

根据所述新地震数据预测砂体厚度。

根据本发明的一个实施例，获取所述偶分量反射系数序列进一步包括：

建立包括地震记录、地震子波、奇偶分解后的地层反射系数的目标函数；

在指定频率范围内，根据所述目标函数对每道地震记录进行运算，以确定对应地层反射系数的偶分量反射系数和奇分量反射系数的位置点和幅值大小；

反复迭代修改偶分量反射系数和奇分量反射系数的位置点和幅值直到满足预设要求，以确定偶分量反射系数序列。

根据本发明的一个实施例，所述目标函数为：

其中，s(t,f)为地震记录；w(t,f)为地震子波；re为偶分量反射系数序列；ro为奇分量反射系数序列；fl为低截频；fh为高截频；n为时窗内包含的地层反射系数的个数；ti为第i层与第n-i+1层之间的间隔；αe和αo为加权系数，t为采样时间，f为主频，re取实部，im取虚部，t为地震道计算时间，re(i,n-i+1)和ro(i,n-i+1)分别表示第i层与第n-i+1层之间的偶分量反射系数序列和奇分量反射系数序列。

根据本发明的一个实施例，合成新地震数据进一步包括：

将所述奇分量反射系数设置为零；

将所述偶分量反射系数序列与所述地震子波进行褶积计算，以得到新地震数据。

根据本发明的一个实施例，根据所述新地震数据预测砂体厚度进一步包括：

根据砂体地震波形结构特征，计算所述新地震数据中每一道地震记录目的层段的地震波谷面积；

统计整个地震数据体的地震波谷面积形成波谷面积的平面累积厚度；

将过井地震道的波形面积与测井解释砂层厚度对比，建立砂体厚度线性对应关系；

以钻井砂体厚度为约束条件，通过插值将波谷面积时间厚度转换为砂体平面厚度。

根据本发明的另一个方面，还提供了一种基于谱反演的砂体厚度预测系统，包括，

数据获取模块，从原始地震数据中获取地震子波和地层反射系数；

反射系数序列获取模块，建立目标函数，并根据所述目标函数、所述地震子 波、奇偶分解后的地层反射系数进行谱反演，以获取偶分量反射系数序列；

新地震数据合成模块，根据所述地震子波、所述偶分量反射系数序列和所述目标函数合成新地震数据；

砂体厚度预测模块，根据所述新地震数据预测砂体厚度。

根据本发明的一个实施例，所述反射系数序列获取模块通过以下步骤获取偶分量反射系数序列：

建立包括地震记录、地震子波、奇偶分解后的地层反射系数的目标函数；

在指定频率范围内，根据所述目标函数对每道地震记录进行运算，以确定对应地层反射系数的偶分量反射系数和奇分量反射系数的位置点和幅值大小；

反复迭代修改偶分量反射系数和奇分量反射系数的位置点和幅值直到满足预设要求，以确定偶分量反射系数序列。

根据本发明的一个实施例，所述目标函数为：

其中，s(t,f)为地震记录；w(t,f)为地震子波；re为偶分量反射系数序列；ro为奇分量反射系数序列；fl为低截频；fh为高截频；n为时窗内包含的地层反射系数的个数；ti为第i层与第n-i+1层之间的间隔；αe和αo为加权系数，t为采样时间，f为主频，re取实部，im取虚部，t为地震道计算时间，re(i,n-i+1)和ro(i,n-i+1)分别表示第i层与第n-i+1层之间的偶分量反射系数序列和奇分量反射系数序列。

根据本发明的一个实施例，所述新地震数据合成模块通过以下步骤合成新地震数据：

将所述奇分量反射系数设置为零；

将所述偶分量反射系数序列与所述地震子波进行褶积计算，以得到新地震数据。

根据本发明的一个实施例，所述砂体厚度预测模块通过以下步骤预测砂体厚度：

根据砂体地震波形结构特征，计算所述新地震数据中每一道地震记录目的层段的地震波谷面积；

统计整个地震数据体的地震波谷面积形成波谷面积的平面累积厚度；

将过井地震道的波形面积与测井解释砂层厚度对比，建立砂体厚度线性对应关系；

以钻井砂体厚度为约束条件，通过插值将波谷面积时间厚度转换为砂体平面厚度。

本发明的有益效果：

本发明的谱反演结果分辨率优于常规反演，其具有无需先验模型、反射系数假设、测井约束等优点，可提高薄层地质目标识别效果，基于谱反演的薄砂体预测方法操作成本低、应用效果好。

本发明的其它特征和优点将在随后的说明书中阐述，并且，部分地从说明书中变得显而易见，或者通过实施本发明而了解。本发明的目的和其他优点可通过在说明书、权利要求书以及附图中所特别指出的结构来实现和获得。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要的附图做简单的介绍：

图1是地层反射系数的奇偶分解原理图；

图2a是地层反射系数及对应的奇偶分量主频与厚度的关系示意图；

图2b是地层反射系数及对应的奇偶分量峰值振幅与厚度的关系示意图；

图3a是地震子波的地层反射系数与对应的奇分量反射系数和偶分量反射系数的关系示意图；

图3b是图3a中三种反射系数的频率和振幅对比关系示意图；

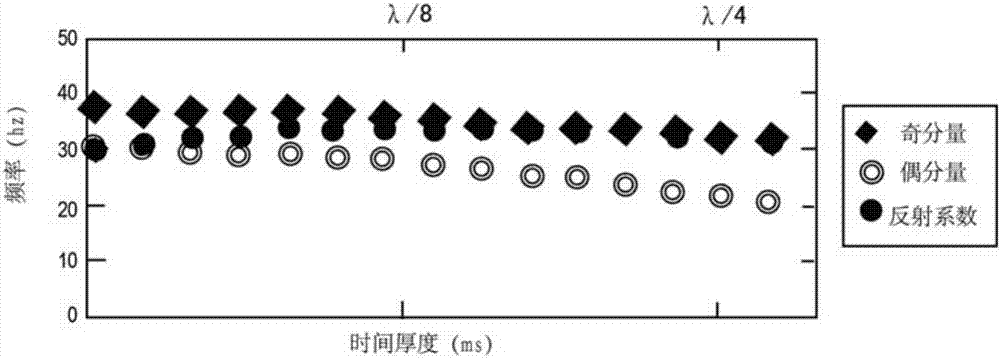
图3c是图3a中三种反射系数的厚度和主频对比关系示意图；

图4是根据本发明的一个实施例的方法流程图；

图5是根据本发明的一个实施例的谱反演求取地层反射系数位置和幅值大小的示意图；

图6是根据本发明的一个实施例的原始地震数据与谱反演数据对比图；

图7是根据本发明的一个实施例的谱反演处理前后的地震剖面对比图；

图8时根据本发明的一个实施例的砂体地质模型及其地震响应特征示意图；

图9是根据本发明的一个实施例的地震波形结构剖面识别河道砂体的示意图；以及

图10是对应图9的河道砂体平面图。

具体实施方式

以下将结合附图及实施例来详细说明本发明的实施方式，借此对本发明如何应用技术手段来解决技术问题，并达成技术效果的实现过程能充分理解并据以实施。需要说明的是，只要不构成冲突，本发明中的各个实施例以及各实施例中的各个特征可以相互结合，所形成的技术方案均在本发明的保护范围之内。

谱反演理论是在谱分解技术结合地震反演，用谱分解获得的局部频谱资料进行反演，计算出薄层反射系数，其反演结果分辨率优于常规反演。将薄层反射系数分解成偶分量和奇分量，通过模型试算已经证明可用来分辨小于调谐厚度(1/4波长)的薄层。当然，该方法也可以用来分辨大于调谐波长的薄层。以下结合附图及理论分析，说明利用地层反射系数的奇分量和偶分量确定砂体厚度的原理。

在地震数据中，有波阻抗差的地层就会产生反射系数，地面接收到的地震记录数据正是反射系数和地震子波褶积的结果。从地震记录数据中去除子波，则可得到地层反射系数。地层反射系数是由一些离散的信号组成，可以分解成一系列偶分量和奇分量，如图1所示为地层反射系数r1和r2各自分解为一个偶分量和一个奇分量的原理图。

如图2a所示为随着地层厚度的减薄，由奇部分量、偶部分量形成的地层反射系数对应模型的主频变化规律。随着地层减薄，地层厚度从调谐厚度(1/4波长)减至调谐厚度一半(1/8波长)时，奇分量和偶分量反射系数的主频先随之增加，然后减小到地震子波的峰值频率30hz。随着地层减薄至零时，主频呈现连续的变化。同时，由图2a可知，奇分量和偶分量反射系数随着地层厚度减小(小于1/4波长)，奇分量与偶分量的主频随地层厚度变化逐渐增大是一个确定关系，表明高频属性更能反映薄层信息。

如图2b所示为当地层厚度从调谐厚度(1/4波长)减至调谐厚度一半(1/8波长)时，在地层厚度为零时，奇部分量、偶部分量形成的反射系数对应的总峰值振幅并不为零，偶分量峰值振幅与总峰值振幅一致。偶分量振幅谱与地层厚度(小于1/4波长)存在倒数对应关系，偶分量更有利于分辨薄层(小于1/4波长)，而奇分量不利于分辨薄层。

因此，地层反射系数经过奇偶分解之后，在地层层厚小于调谐厚度一半(1/8 波长)后，奇分量与偶分量的主频随地层厚度变化逐渐增大是一个确定关系。在地震资料主频确定的情况下，反射系数通过奇偶分解可以准确预测小于调谐厚度下的薄层厚度。但偶分量和奇分量有不同的薄层频谱响应特征和分辨能力，偶分量能够明显提高薄层的分辨率，而奇分量反射系数不利于分辨薄层。

如图3a所示为采集到的一个地震子波的地层反射系数与对应奇偶分解之后的奇分量反射系数和偶分量反射系数的关系示意图，偶分量反射系数合成的地震子波波形与原始地层反射系数对应的波形近似，而奇分量反射系数相差较远。如图3b所示，地层反射系数奇偶分解后，偶分量频率峰值与地层反射系数频率峰值一致，奇分量频率峰值更低。如图3c所示为三种不同反射系数识别实际地层厚度的差别示意图，可知偶分量识别的地层时间厚度与实际地层厚度误差小、精度高，奇分量识别的地层时间厚度与实际地层厚度误差大。

因此，基于以上原理，本发明提供了一种基于谱反演的厚度小于1/4波长薄砂体的预测方法，用于提高厚度小于1/4波长的薄层砂体厚度的预测精度。当然，本发明也可以用来预测厚度大于1/4波长的砂体厚度。

如图4所示为根据本发明的一个实施例的一种基于谱反演的砂体厚度预测方法流程图，以下参考图4来对本发明进行详细说明。

首先，在步骤s110中，从原始地震数据中获取地震子波和地层反射系数。具体的，在该步骤中，从原始地震数据中精确的提取地震子波，避免出现由非地质成因而产生的假象，减少地震子波对反演结果的影响。虽然地震子波一般是未知的，但地震数据中包含有子波信息，可以采用无井控制统计方法从地震记录中求取子波，该方法不需要测井信息也能得到子波。在采用以上无井控制统计方法求取地震子波时，采用的理论模型为：

s(t)＝r(t)*w(t)(1)

其中，s(t)为地震记录，r(t)为地层反射系数，w(t)为地震子波。设定初始r(t)和w(t)的值，经反复迭代和修改得到与原始地震记录拟合度最好的s(t)，此时对应的r(t)和w(t)即为所求的地层反射系数和地震子波。

接下来，在步骤s120中，建立目标函数，并根据目标函数、地震子波、奇偶分解后的地层反射系数进行谱反演，以获取偶分量反射系数序列。

在步骤s110中得到的地层反射系数是一系列离散的信号，此时的地层反射系数是无序的，无法与地层进行对应。因此，在步骤s120中，通过将地层反射 系数进行奇偶分解，并通过谱反演获取与地层序列对应的偶分量反射系数序列。

谱反演的原理就是根据时间域褶积模型，从地震记录中去除地震子波的影响，进而得到反射系数序列的奇分量和偶分量。在本发明中，假设地层波阻抗模型所对应的反射系数序列模型是稀疏分布的，即地震反射系数是由起主导作用的强反射系数序列和具有高斯背景的弱反射系数序列(薄互层)叠加而成，如图5所示。谱反演是将地震记录进行反褶积去除子波得到地层反射系数，求得具有稀疏特性的反射系数序列。谱反演需要建立目标函数，求解目标函数的过程就是去除地震子波，并确定反射系数奇、偶性和反射系数值的大小。

具体的，获取与地层序列对应的偶分量反射系数序列包括以下的几个步骤。首先建立目标函数，该目标函数包括地震记录、地震子波、奇偶分解后的地层反射系数的目标函数：

其中，s(t,f)为地震记录；w(t,f)为地震子波；re为偶分量反射系数序列；ro为奇分量反射系数序列；fl为低截频；fh为高截频；n为时窗内包含的地层反射系数的个数；ti为第i层与第n-i+1层之间的间隔；αe和αo为加权系数，t表示采样时间，f表示主频，re取实部，im取虚部，t表示地震道计算时间，re(i,n-i+1)和ro(i,n-i+1)分别表示第i层与第n-i+1层之间的偶分量反射系数序列和奇分量反射系数序列。

接着，在指定频率范围fl-fh内，根据目标函数对每道地震记录进行运算，以确定对应地层反射系数的偶分量反射系数和奇分量反射系数的位置点和幅值大小。具体的，将偶分量反射系数和奇分量反射系数的位置点和幅值代入目标函数式(1)中，使得目标函数的值接近零，这样可以初步获得多组偶分量反射系数序列和奇分量反射系数序列。

接着，反复迭代修改偶分量反射系数和奇分量反射系数的位置点和幅值直到满足预设要求，以确定偶分量反射系数序列。具体的，通过反复迭代修改每个地层反射系数(奇分量和偶分量反射系数合成地层反射系数)的位置点和幅度，以使得与地震子波褶积运算后得到一个与实际地震资料达到最佳逼近的合成地震 记录，最终获得宽频带内的偶分量反射系数序列分布。

接下来，在步骤s130中，根据地震子波、偶分量反射系数序列和目标函数合成新地震数据。具体的，将奇分量反射系数设置为零，将偶分量反射系数序列与地震子波进行褶积计算，以得到新地震数据。如图6所示为原始地震数据与谱反演数据的井震标定对比图，可知谱反演数据保留了原始地震数据的强反射特征，峰值频率从30hz拓宽到40hz。结合井震标定，可发现偶分量反射系数提高了薄层识别效果，且符合测井解释对应的地层特征。图7所示为谱反演处理前后的地震剖面对比图，由图7所示，谱反演处理后地震资料频带变宽、主频提高，薄层识别能力增强。wb37井有两套薄砂体，在原始地震资料上是不能分开的(图7中a部分)，而处理后则可清晰的识别(图7中的b部分)，能够满足厚度小于λ/4的薄层识别需求。

最后，在步骤s140中，根据新地震数据预测砂体厚度。具体的，计算新地震数据中每一道地震记录目的层段的地震波谷面积，统计整个地震数据体的波谷面积形成波谷面积的平面累积厚度，将过井地震道的波形面积与测井解释砂层厚度对比，建立砂体厚度线性对应关系，以钻井砂体厚度为约束条件，通过插值将波谷面积时间厚度转换为砂体平面厚度。

以下通过一个具体的例子来说明如何根据新地震数据预测砂体厚度。如图8所示为根据本发明的一个实施例的砂体地质模型及其地震响应特征示意图，通过地震正演模拟三套砂体纵向厚度及横向变化特征，明确河道砂体地震波形结构特征模型。与原始地震数据相比，谱反演地震数据分辨率明显提高，其主频提高了10hz、频带拓宽了20hz，强反射界面更清楚，弱反射界面显著增强。地质模型中第一套砂体厚0-15m，第二套砂体厚0-20m，第三套砂体厚0-10m，其中泥岩速度2500m/s，砂岩速度3000m/s。正演模型结果表明，20m厚砂体对应的波谷最宽、面积最大；随着砂体厚度减薄，波谷变窄、面积变小。

图9所示为地震波形结构剖面识别河道砂体示意图，可发现河道砂体层厚规模与波谷波形面积具有较好的对应关系，砂体厚度越大对应波谷面积越大，连续性越好；砂泥薄互层对应波谷面积小，连续性差。根据剖面上波谷地震波形结构特征识别和预测了过井位置和井间的河道砂体发育特征，20m以上砂体和20m以下砂体(小于1/4波长)都可以识别和预测，表明基于谱反演数据的河道薄砂体预测技术具有很好的实用性。图10所示为地震波形结构预测河道砂体平面图。 在开发区外围有三个20m以下河道砂体发育区，是油田下一步开发调整和产量接替的有利阵地。

在本发明中，谱反演结果分辨率优于常规反演，其具有无需先验模型、反射系数假设、测井约束等优点，可提高薄层地质目标识别效果，基于谱反演的薄砂体预测方法操作成本低、应用效果好。

根据本发明的另一个方面，还提供了一种基于谱反演的砂体厚度预测系统，该系统，包括数据获取模块、反射系数序列获取模块、新地震数据合成模块和砂体厚度预测模块。

其中，数据获取模块从原始地震数据中获取地震子波和地层反射系数；反射系数序列获取模块建立目标函数，并根据目标函数、地震子波、奇偶分解后的地层反射系数进行谱反演，以获取偶分量反射系数序列；新地震数据合成模块根据所述地震子波、偶分量反射系数序列和所述目标函数合成新地震数据；砂体厚度预测模块根据新地震数据预测砂体厚度。

在本发明的一个实施例中，反射系数序列获取模块通过以下步骤获取偶分量反射系数序列：建立包括地震记录、地震子波、奇偶分解后的地层反射系数的目标函数；在指定频率范围fl-fh内，根据目标函数对每道地震记录进行运算，以确定对应地层反射系数的偶分量反射系数和奇分量反射系数的位置点和幅值大小；反复迭代修改偶分量反射系数和奇分量反射系数的位置点和幅值直到满足预设要求，以确定偶分量反射系数序列。

在本发明的一个实施例中，该目标函数如式(2)所示。

在本发明的一个实施例中，该新地震数据合成模块通过以下步骤合成新地震数据：将奇分量反射系数设置为零；将偶分量反射系数序列与所述地震子波进行褶积计算，以得到新地震数据。

在本发明的一个实施例中，砂体厚度预测模块通过以下步骤预测砂体厚度：根据砂体地震波形结构特征，计算所述新地震数据中每一道地震记录目的层段的地震波谷面积；统计整个地震数据体的地震波谷面积形成波谷面积的平面累积厚度；将过井地震道的波形面积与测井解释砂层厚度对比，建立砂体厚度线性对应关系；以钻井砂体厚度为约束条件，通过插值将波谷面积时间厚度转换为砂体平面厚度。

虽然本发明所公开的实施方式如上，但所述的内容只是为了便于理解本发明 而采用的实施方式，并非用以限定本发明。任何本发明所属技术领域内的技术人员，在不脱离本发明所公开的精神和范围的前提下，可以在实施的形式上及细节上作任何的修改与变化，但本发明的专利保护范围，仍须以所附的权利要求书所界定的范围为准。