一种用于无线传感器网络的分布式多源定位算法的制作方法

本发明涉及无线传感器网络多源定位领域，具体是一种用于无线传感器网络的分布式多源定位算法。
背景技术：
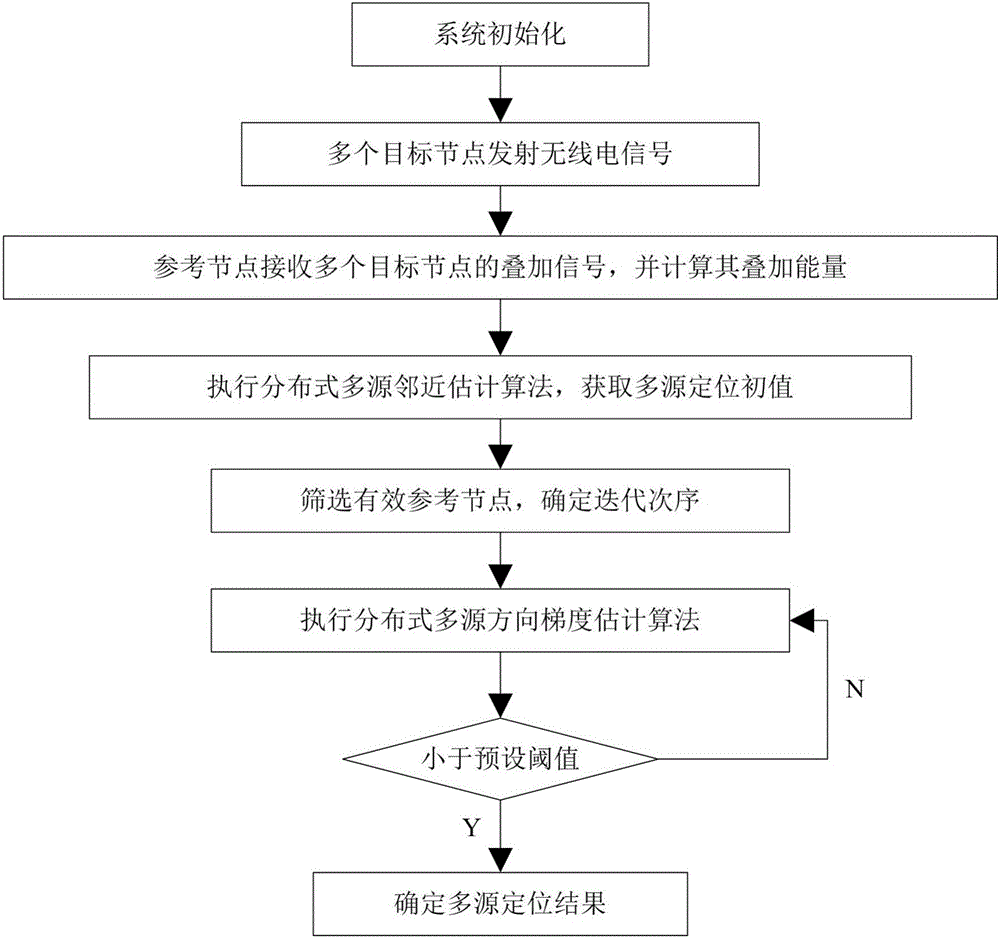
：无线传感器网络无处不在，其中基于位置的服务是无线传感器网络中非常重要的应用方向，涉及个人导航、医护监控、突发情况救援、商业和社交等各个领域，用户和服务商对于位置信息均有较高的需求，因此关于无线定位技术的研究一直深受关注。从数据处理方式的角度来看，定位方法可以分为集中式定位和分布式定位。集中式方法可充分利用所有的信息以及信息之间的耦合性，因此定位性能更好，但是所有节点向数据中心传递原始数据，通信能耗较高，并且数据中心的计算复杂度也较高。而分布式方法直接对本地数据进行处理，避免了逐级传递造成的通信能耗，特别是在大规模网络中，这种通信能耗不可忽视，分布式的方法会大大提高能量利用率，但由于在每个节点进行数据处理时采用的是部分测量信息，不能充分考虑到全局信息之间的关系，因此定位性能往往较集中式定位差。从定位目标节点的数量来看，可以分为单点定位和多源定位。对于单点定位的研究比较广泛且成熟，包括集中式和分布式的方法。由于传感器网络中的节点多为电池供电，能量有限，应该尽可能地减少消耗，因此分布式的单点定位算法引起许多学者的关注。在文献《Energy-BasedSensorNetworkSourceLocalizationviaProjectionOntoConvexSets》中，最小二乘问题被表述为凸可行性问题，提出一种分布式的POCS方法，表现出更快的全局收敛特性。然而当定位区域内存在多个目标节点时，若以单点定位的方式来逐一定位，会造成巨大的能耗浪费，效率极低，是不实际的。并且在大多数无线传感器网络定位系统中，为了降低设备成本以及能量消耗，节点往往得到的是来自多个目标节点的信号叠加，而不是每个目标节点独立的信号，这样定位的复杂度增加，单点定位的算法不能简单地扩展到多点定位上。目前，对于多源定位的研究多是集中式的。具体地，文献《MaximumLikelihoodMultiple-SourceLocalizationUsingAcousticEnergyMeasurementswithWirelessSensorNetworks》给出了基于能量的集中式多源定位模型，并提出了两种解决算法，多分辨率搜索算法和迭代期望最大化算法，降低了集中式定位算法的复杂度。文献《MultipleSourceLocalizationinWirelessSensorNetworksBasedonTimeofArrivalMeasurements》则使用TOA测量值，研究在未知测量信号到达时间和源点之间的关系以及未知源点信号发射初始时间的情况下的多源定位问题，计算复杂度较高。综上所述，目前尚缺少适用于无线传感器网络的分布式多源定位方法。因此，需要一种分布式的多源位置解算方法，降低通信能耗，以应对无线传感器网络能量限制。技术实现要素：针对现有技术的不足，本发明公开了一种用于无线传感器网络的分布式多源定位算法，应对无线传感器网络中多源位置解算的需求，同时解决传统集中式多源定位方法通信能耗较大、计算复杂度较高的问题。本发明的技术方案如下：一种用于无线传感器网络的分布式多源定位算法，包括以下步骤：(1)系统初始化；(2)无线传感器网络中多个目标节点发射无线电信号，参考节点接收多源叠加信号，并计算叠加能量，确定多源定位模型；(3)执行分布式多源邻近估计算法，获取多源定位初值；(4)根据步骤(3)所获得的多源定位初值筛选有效参考节点，确定下一步的迭代运算次序；(5)执行分布式多源方向梯度估计算法，按照步骤(4)所确定的参考节点迭代次序，在上一次迭代位置估计值处，对自身能量测量值进行多源方向梯度运算，并解算本次迭代位置估计值；(6)将每次迭代定位结果和上一次迭代定位结果的差值与系统预设阈值比较，若差值大于或者等于系统预设阈值，则返回步骤(5)，重新执行分布式多源方向梯度估计算法；若差值小于系统预设阈值，则本次迭代位置估计值即为最终多源定位结果。其进一步的技术方案为，所部步骤(1)中，系统初始化包括对采样周期T、采样数N，邻近估计算法随机向量Δ，邻近节点距离阈值ζ，信噪比阈值τ，迭代步长α和误差阈值ε的预设。其进一步的技术方案为，所述步骤(2)具体为：设定二维的无线传感器网络，内部分布着P个参考节点BS，坐标为：R={[r1,r2,...,rp,...,rP]T∈RP×2,p=1,2,...P};]]>M个待定位的目标节点MS，坐标为：θ={[ρ1,ρ2,...,ρm,...,ρM]T∈RM×2,m=1,2,...M};]]>目标节点周期性发射相同的无线电信号s(n)，设参考节点的接收增益均为1，则参考节点p接收到目标节点m的信号能量为：yp(m)(n)=s(n)||ρm-rp||2+vp(n);]]>其中，vp(n)为参考节点p处的加性噪声，服从正态分布N(0,σ2)；因此，参考节点p接收到的多源信号能量的叠加为：yp(n)=Σm=1M[s(n)||ρm-rp||2+vp(n)];]]>取采样周期T内的信号能量叠加平均值yp，并认为在采样周期T内则：yp=Σm=1Ms||ρm-rp||2+wp,]]>其中：wp=ΔΣm=1Mvp~N(0,Mσ2);]]>将P个参考节点的信号能量叠加平均值，即能量测量值，以矩阵的形式表示：Y=Δ[y1,y2,...,yP]T∈RP×1,]]>S=Δ[s,s,...,s]T∈RM×1,]]>W=Δ[w1,w2,...,wP]T∈RP×1,]]>D=Δ1/(d1(1))2,1/(d1(2))2,...,1/(d1(M))21/(d2(1))2,1/(d2(2))2,...,1/(d2(M))2............1/(dP(1))2,1/(dP(2))2,...,1/(dP(M))2∈RP×M,]]>其中：dp(m)=Δ||ρm-rp||,]]>则P个参考节点的能量测量值矩阵可表示为：Y＝DS+W。其进一步的技术方案为，所述步骤(3)具体为：(3a)令m＝1；(3b)将无线传感器网络内的参考节点1将自身的能量测量值赋值给ymax；并将自身的节点序号赋值给目标节点m对应的邻近参考节点序号估计值；(3c)按照参考节点的序号顺序，将ymax和目标节点m的邻近节点序号估计值依次向下传递；(3d)参考节点p接收来自参考节点p-1处传来的ymax和目标节点m的邻近节点序号估计值；(3e)参考节点将自身的能量测量值与ymax作比较，更新ymax和目标节点m的邻近节点序号估计值；(3f)判断是否遍历所有参考节点，如果未遍历所有参考节点，则重复步骤(3c)至步骤(3e)；当遍历所有的参考节点之后，确定目标节点m的位置估计初值，并更新所有参考节点的能量测量值；(3g)使m＝m+1，并判断是否到达最后一个目标节点，如果m＞M，则输出所有目标节点的位置估计初值；如果m＜M，则重复步骤(3b)至步骤(3f)，对下一个目标节点进行估计。其进一步的技术方案为，所述步骤(3e)具体为：首先，根据参考节点的信号能量叠加平均值估计第一个目标节点的位置初值；设M个目标节点对应的邻近参考节点序号集合为：Ind^=[Ind^(1),Ind^(2),...,Ind^(M)]T∈RM×1,]]>yp0=yp,p=1,2,...,P,]]>则第一个目标节点的邻近参考节点序号为：Ind^(1)=argmaxyp0p,]]>在邻近参考节点坐标上附加随机向量Δ，则第一个目标节点的位置初值估计为：ρ^1(0)=rInd^(1)+Δ;]]>根据第一个目标节点的初值更新所有参考节点的能量测量值：yp1=yp0-s||ρ^1(0)-rp||2,p≠Ind^(1)yp0-sζ2,p=Ind^(1),]]>其中，ζ为邻近节点距离阈值；其次，根据第一个目标节点的位置初值，求得第二个目标节点的位置初值：第二个目标节点的邻近参考节点序号为：Ind^(2)=argmaxyp1,]]>第二个目标节点的位置初值估计为：ρ^2(0)=rInd^(2)+Δ,]]>根据第二个目标节点的初值更新所有参考节点的能量测量值：yp2=yp1-s||ρ^1(0)-rp||2,p≠Ind^(2)yp1-sζ2,p=Ind^(2),]]>依此类推，最后，第m个目标节点的邻近参考节点序号为：Ind^(m)=argmaxypm-1,]]>第m个目标节点的位置初值估计为：ρ^m(0)=rInd^(m)+Δ,]]>根据第m个目标节点的初值更新所有参考节点的能量测量值：ypm=ypm-1-s||ρ^m-1(0)-rp||2,p≠Ind^(m-1)ypm-1-sζ2,p=Ind^(m-1),]]>即，将所有参考节点的能量测量值更新为其进一步的技术方案为，所述步骤(4)具体为：设定接收信号的信噪比大于信噪比阈值τ的参考节点为有效参考节点，数量为K，并将所筛选的有效参考节点按照能量值大小，重新排列其序号；有效参考节点坐标为：{[r1,r2,…,rk,…,rK]T∈RK×2,k＝1,2,…K}；K个有效参考节点的能量测量值矩阵为：Y＝DS+W，其中，Y=Δ[y1,y2,...,yK]T∈RK×1,]]>S=Δ[s,s,...,s]T∈RM×1,]]>W=Δ[w1,w2,...,wK]T∈RK×1,]]>D=Δ1/(d1(1))2,1/(d1(2))2,...,1/(d1(M))21/(d2(1))2,1/(d2(2))2,...,1/(d2(M))2............1/(dK(1))2,1/(dK(2))2,...,1/(dK(M))2∈RK×M.]]>其进一步的技术方案为，在所述步骤(5)中，分布式多源方向梯度估计算法具体为：在多源坐标信息θ下，K个有效参考节点的能量测量值yk的联合概率密度函数为：f(Y|θ)=(12πMσ)K·exp[-12Mσ2(Y-DS)T(Y-DS)],]]>令目标函数l(θ)＝||Y-DS||2，θ为待求解的多源坐标；以分布式的方法进行解算，则有效参考节点k处的目标函数为：lk(θ)＝(Yk-DkS)2，分别对目标节点m进行方向梯度解算，计算公式为：∂lk(θ)∂ρm,]]>执行分布式多源方向梯度估计算法，按照步骤(4)所确定的有效参考节点序号进行目标节点坐标估计；其步骤具体为：(5a)令i＝1；(5b)令有效参考节点k＝1；目标节点m的坐标估计为：ρ^m(i)=ρ^m(i-1)-α·∂lk(θ)∂ρm|ρm=ρ^m(i-1);]]>(5c)令k＝k+1，重复步骤(5b)，直至k＝K，循环停止，目标节点m的坐标估计值更新为：ρ^m(i)=ρ^m(i-1)-α·∂lK(θ)∂ρm|ρm=ρ^m(i-1);]]>(5d)令i＝i+1，重复步骤(5b)和步骤(5c)，之后进行步骤(6)。其进一步的技术方案为，所述步骤(6)具体为：每执行步骤(5d)之后，则进行步骤(6)，将目标节点m的坐标更新值和上一次循环迭代得到的目标节点m的坐标值的差值与系统预设定位误差阈值ε作比较，若差值大于或者等于系统预设阈值ε，则返回步骤(5d)，重新执行分布式多源方向梯度估计算法；若差值小于系统预设阈值ε，则本次迭代位置估计值即为最终目标节点m的定位结果。本发明的有益技术效果是：1、本发明采用分布式解算方法，不需要数据中心，降低了由原始测量数据传输带来的通信能耗，可有效应对无线传感器网络能量限制问题。2、本发明采用能量测量值进行多源坐标解算，不会增加额外的硬件成本，对时钟精度的要求也较低。3、与传统最近节点算法(CPA，ClosestPointApproach)相比，本发明涉及的分布式多源邻近估计算法具有较好的邻近节点分辨能力，而传统CPA算法无法分辨相距较近的目标节点。4、本发明涉及的分布式多源方向梯度估计算法采用多源并行计算方式，在保证算法时效性与系统定位容量的同时降低了系统计算复杂度。附图说明图1为本发明的流程图。图2为无线传感器网络多源定位环境二维示意图。图3为本发明中分布式多源邻近估计算法流程图。图4为本发明中分布式多源邻近估计算法与传统CPA算法仿真结果对比图。图5为本发明中分布式多源方向梯度估计算法流程图。图6为本发明定位性能仿真结果图。具体实施方式本发明所述的算法，不需要数据中心，而是由无线传感器网络中各个节点以迭代的形式参与运算，进行多源定位。图1为本发明的流程图。如图1所示，本发明所述的算法包括以下步骤：(1)系统初始化。系统初始化包括采样周期T、采样数N、邻近估计算法随机向量Δ、邻近节点距离阈值ζ、信噪比阈值τ、迭代步长α和误差阈值ε的预设。(2)无线传感器网络中多个目标节点发射无线电信号，参考节点接收多源叠加信号，并计算叠加能量，确定多源定位模型。图2为无线传感器网络多源定位环境二维示意图。如图2所示，考虑一个二维的无线传感器网络，内部分布着P个参考节点BS，坐标为：R＝{[r1,r2,…,rp,…,rP]T∈RP×2,p＝1,2,…P}；M个待定位的目标节点MS，坐标为：θ＝{[ρ1,ρ2,…,ρm,…,ρM]T∈RM×2,m＝1,2,…M}。目标节点周期性发射相同的无线电信号s(n)，设参考节点的接收增益均为1，则参考节点p接收到目标节点m的信号能量为：yp(m)(n)=s(n)||ρm-rp||2+vp(n);]]>其中，vp(n)为参考节点p处的加性噪声，服从正态分布N(0,σ2)。因此，参考节点p接收到的多源信号能量的叠加为：yp(n)=Σm=1M[s(n)||ρm-rp||2+vp(n)];]]>取采样周期T内的多源信号能量叠加平均值yp，并认为在采样周期T内则：yp=Σm=1Ms||ρm-rp||2+wp,]]>其中：wp=ΔΣm=1Mvp~N(0,Mσ2).]]>将P个参考节点的多源信号能量叠加平均值，以矩阵的形式表示：Y=Δ[y1,y2,...,yP]T∈RP×1,]]>S=Δ[s,s,...,s]T∈RM×1,]]>W=Δ[w1,w2,...,wP]T∈RP×1,]]>D=Δ1/(d1(1))2,1/(d1(2))2,...,1/(d1(M))21/(d2(1))2,1/(d2(2))2,...,1/(d2(M))2............1/(dP(1))2,1/(dP(2))2,...,1/(dP(M))2∈RP×M,]]>其中：dp(m)=Δ||ρm-rp||,]]>则P个参考节点的能量测量值矩阵，即多源信号能量叠加平均值矩阵，可表示为：Y＝DS+W。(3)执行分布式多源邻近估计算法，获取多源定位初值。图3为本发明中分布式多源邻近估计算法流程图。如图3所示，步骤(3)具体为：(3a)令m＝1；(3b)将无线传感器网络内的参考节点1将自身的能量测量值赋值给ymax；并将自身的节点序号赋值给目标节点m对应的邻近参考节点序号估计值。具体的，针对m＝1的情况，将无线传感器网络内的参考节点1将自身的能量值赋值给ymax，令并将自身的节点序号赋值给目标节点m对应的邻近参考节点序号估计值，使之为(3c)按照参考节点的序号顺序，将ymax和目标节点m的邻近节点序号估计值依次向下传递；(3d)参考节点p接收来自参考节点p-1处传来的ymax和目标节点m的邻近节点序号估计值；(3e)参考节点将自身的能量测量值与ymax作比较，更新ymax和目标节点m的邻近节点序号估计值。步骤(3e)具体为：首先，根据参考节点的信号能量叠加平均值估计第一个目标节点的位置初值；设M个目标节点对应的邻近参考节点序号集合为：Ind^=[Ind^(1),Ind^(2),...,Ind^(M)]T∈RM×1,]]>yp0=yp,p=1,2,...,P,]]>则第一个目标节点的邻近参考节点序号为：Ind^(1)=argmaxyp0p,]]>在邻近参考节点坐标上附加随机向量Δ，则第一个目标节点的位置初值估计为：ρ^1(0)=rInd^(1)+Δ.]]>根据第一个目标节点的初值更新所有参考节点的能量测量值：yp1=yp0-s||ρ^1(0)-rp||2,p≠Ind^(1)yp0-sζ2,p=Ind^(1),]]>其中，ζ为邻近节点距离阈值；其次，根据第一个目标节点的位置初值，求得第二个目标节点的位置初值：第二个目标节点的邻近参考节点序号为：Ind^(2)=argmaxyp1,]]>第二个目标节点的位置初值估计为：ρ^2(0)=rInd^(2)+Δ,]]>根据第二个目标节点的初值更新所有参考节点的能量测量值：yp2=yp1-s||ρ^1(0)-rp||2,p≠Ind^(2)yp1-sζ2,p=Ind^(2),]]>依此类推，第m个目标节点的邻近参考节点序号为：Ind^(m)=argmaxypm-1,]]>第m个目标节点的位置初值估计为：ρ^m(0)=rInd^(m)+Δ,]]>根据第m个目标节点的初值更新所有参考节点的能量测量值：ypm=ypm-1-s||ρ^m-1(0)-rp||2,p≠Ind^(m-1)ypm-1-sζ2,p=Ind^(m-1),]]>即，将所有参考节点的能量测量值更新为(3f)判断是否遍历所有参考节点，如果未遍历所有参考节点，则重复步骤(3c)至步骤(3e)，当遍历所有的参考节点之后，确定目标节点m的位置估计初值，并更新所有参考节点的能量测量值。具体的，针对m＝1的情况，当遍历所有的参考节点之后，在参考节点P处得到网络内最大能量测量值ymax和对应参考节点信息(3g)使m＝m+1，并判断是否到达最后一个目标节点，如果m＞M，则输出所有目标节点的位置估计初值，如果m＜M，则重复步骤(3b)至步骤(3f)，对下一个目标节点进行估计。无线传感器网络参考节点每完成一次循环迭代，一个目标节点的初值即被确定，然后再进行下一次循环迭代，更新所有参考节点的能量测量值，直到完成所有M个目标节点的初值估计，分布式多源邻近估计算法结束。当到达最后一个目标节点时，得到所有目标节点的位置估计初值为：θ^(0)=[ρ^1(0),ρ^2(0),...,ρ^M(0)]T∈RM×2.]]>图4为本发明中分布式多源邻近估计算法与传统CPA算法仿真结果对比图。本发明涉及的分布式多源邻近估计算法具有较好的邻近节点分辨能力，而传统CPA算法无法分辨相距较近的目标节点。(4)根据步骤(3)所获得的多源定位初值筛选有效参考节点，确定下一步的迭代运算次序。设定接收信号的信噪比大于信噪比阈值τ的参考节点为有效参考节点，数量为K，并将所筛选的有效参考节点按照能量值大小，重新排列其序号，之后的迭代次序按照新排列的有效参考节点排序进行。则有效参考节点坐标为：{[r1,r2,…,rk,…,rK]T∈RK×2,k＝1,2,…K}。K个有效参考节点的能量测量值矩阵为：Y＝DS+W，其中，Y=Δ[y1,y2,...,yK]T∈RK×1,]]>S=Δ[s,s,...,s]T∈RM×1,]]>W=Δ[w1,w2,...,wK]T∈RK×1,]]>D=Δ1/(d1(1))2,1/(d1(2))2,...,1/(d1(M))21/(d2(1))2,1/(d2(2))2,...,1/(d2(M))2............1/(dK(1))2,1/(dK(2))2,...,1/(dK(M))2∈RK×M.]]>(5)执行分布式多源方向梯度估计算法，按照步骤(4)所确定的有效参考节点迭代次序，在上一次迭代位置估计值处，对自身能量测量值进行多源方向梯度运算，并解算本次迭代位置估计值。在多源坐标信息θ下，K个有效参考节点的能量测量值yk的联合概率密度函数为：f(Y|θ)=(12πMσ)K·exp[-12Mσ2(Y-DS)T(Y-DS)],]]>令目标函数l(θ)＝||Y-DS||2，则当l(θ)取最小值时，f(Yθ)最大，此时θ便是待求解的多源坐标。以分布式的方法进行解算，则有效参考节点k处的目标函数为：lk(θ)＝(Yk-DkS)2，分别对目标节点m进行方向梯度解算，计算公式为：∂lk(θ)∂ρm,]]>并以增量梯度迭代的方式，按照步骤(4)所确定的有效参考节点运算次序进行目标节点坐标估计。其步骤具体为：(5a)进行第1次循环，令i＝1；(5b)令有效参考节点k＝1；目标节点m的坐标估计为：ρ^m(i)=ρ^m(i-1)-α·∂lk(θ)∂ρm|ρm=ρ^m(i-1).]]>(5c)令k＝k+1，重复步骤(5b)，直至k＝K，循环停止，目标节点m的坐标估计值更新为：ρ^m(i)=ρ^m(i-1)-α·∂lK(θ)∂ρm|ρm=ρ^m(i-1);]]>(5d)令i＝i+1，重复步骤(5b)和步骤(5c)，之后进行步骤(6)。即，在上述步骤(5b)，步骤(5c)中，在进行第1次循环时，即i＝1时，对K个有效参考节点进行迭代计算，从有效参考节点k＝1处开始，目标节点m的坐标估计为：ρ^m(1)=ρ^m(0)-α·∂l1(θ)∂ρm|ρm=ρ^m(0),]]>之后将赋值给依次向下传递，即，使得k＝k+1，在有效参考节点k处，目标节点m的坐标估计为：ρ^m(1)=ρ^m(0)-α·∂lk(θ)∂ρm|ρm=ρ^m(0),]]>将赋值给继续向下传递，完成第一次循环迭代后，共经过了K次迭代，即，当k＝K时，在有效参考节点K处，目标节点m的坐标更新为：ρ^m(1)=ρ^m(0)-α·∂lK(θ)∂ρm|ρm=ρ^m(0).]]>此时即i＝1时的循环结束。之后使得i＝i+1，继续进行下一次增量梯度迭代计算，计算方法可参见上述i＝1时的情况，对所有有效参考节的坐标进行更新。第i次分布式多源方向梯度算法循环迭代后目标节点m的坐标估计值更新为：ρ^m(i)=ρ^m(i-1)-α·∂lK(θ)∂ρm|ρm=ρ^m(i-1).]]>之后进行步骤(6)。(6)将每次迭代定位结果和上一次迭代定位结果的差值与系统预设阈值比较，若差值大于或者等于系统预设阈值，则返回步骤(5d)，重新执行分布式多源方向梯度估计算法；若差值小于系统预设阈值，则本次迭代位置估计值即为最终多源定位结果。具体的，每执行步骤(5d)中的一次循环迭代之后，则进行步骤(6)，将目标节点m的坐标更新值和上一次循环迭代得到的目标节点m的坐标值的差值与系统预设定位误差阈值ε作比较，若差值大于或者等于系统预设阈值ε，则返回步骤(5d)，重新执行分布式多源方向梯度估计算法；若差值小于系统预设阈值ε，则本次迭代位置估计值即为最终目标节点m的定位结果。图5为本发明中分布式多源方向梯度估计算法流程图，步骤(5)和步骤(6)的流程可参见图5。最终，分布式多源定位算法所解算所确定的的多源坐标为：θ^=[ρ^1,ρ^2,...,ρ^M]T∈RM×2.]]>图6为本发明定位性能仿真结果图，仿真有效参考节点数量为36，循环迭代次数为1次，可见本发明采用多源并行分布式解算方法，有效降低了由原始测量数据传输带来的通信能耗，在循环迭代次数较少的情况下也能保证一定的定位精度和定位容量，同时降低了系统计算复杂度。以上所述的仅是本发明的优选实施方式，本发明不限于以上实施例。可以理解，本领域技术人员在不脱离本发明的精神和构思的前提下直接导出或联想到的其他改进和变化，均应认为包含在本发明的保护范围之内。当前第1页1 2 3