基于地面目标点位置的卫星姿态角的计算方法与流程

本发明属于航天测量与控制应用领域，涉及航天器对地面目标观测的姿态机动计算方法，适用于地球资源航天器及遥感航天器在飞行过程中对地面目标观测的姿态机动计算。
背景技术：
：随着空间对地观测技术的迅猛发展，遥感航天器越来越多，对地面目标的访问模式也由以往的固定星下点模式、单侧摆模式发展可多自由度姿态调节传感器模式。以往的固定星下点模式、单侧摆模式无法对同时能够两个方向、多自由度姿态调节传感器模式进行建模计算，且计算过程冗长复杂。随着新型航天器和传感器的出现，需要研究新的可多自由度姿态调节的对地面目标观测姿态机动计算方法。技术实现要素：本发明所要解决的技术问题是航天器对地面目标观测的姿态计算方法，建立了地面目标点和卫航天器坐标转换关系，依据空间几何关系给出了航天器对地面目标观测的方程，并得到了该方程的分析解，计算航天器观测该目标所需姿态。该结果可用于多自由度姿态调节传感器模式的航天器对地面目标观测的姿态计算中。本发明采用的技术方案为：基于地面目标点位置的卫星姿态角的计算方法，包括以下步骤：(1)将地面目标点在大地坐标系中的经度、纬度和高程转换为地固坐标系中的直角坐标；(2)将地面目标点在地固坐标系中的直角坐标转换为地心J2000惯性坐标系中的位置矢量；(3)根据卫星在地心J2000惯性坐标系中的位置速度矢量和速度矢量求出地心J2000惯性坐标系到卫星轨道坐标系的转换矩阵C；(4)用转换矩阵C将地面目标点在地心J2000惯性坐标系中的位置矢量转换成卫星在轨道坐标系中的位置矢量；(5)根据地面目标点在卫星轨道坐标系中的位置矢量求得卫星的姿态角；完成基于地面目标点位置的卫星姿态角的计算。其中，步骤(5)具体为：卫星绕X轴旋转时的姿态旋转角为横滚角绕Y轴旋转时的姿态旋转角为俯仰角θ，绕Z轴旋转时的姿态旋转角为偏航角ψ；卫星绕两个轴旋转，有以下四种方法可得到卫星的姿态角；方法1：卫星先绕Y轴旋转，再绕X轴旋转；由：得式中，(x,y,z)为地面目标点在卫星轨道坐标系中的位置矢量，r为位置矢量(x,y,z)的绝对值；方法2：卫星先绕X轴旋转，再绕Y轴旋转：由：得式中，(x,y,z)为地面目标点在卫星轨道坐标系中的位置矢量，r为位置矢量(x,y,z)的绝对值；方法3：卫星先绕Z轴旋转，再绕Y轴旋转：由xyz=sinθcosψsinθsinψcosθ]]>得式中，(x,y,z)为地面目标点在卫星轨道坐标系中的位置矢量，r为位置矢量(x,y,z)的绝对值；方法4：卫星先绕Z轴旋转，再绕X轴旋转：由得式中，(x,y,z)为地面目标点在卫星轨道坐标系中的位置矢量，r为位置矢量(x,y,z)的绝对值。与
背景技术：
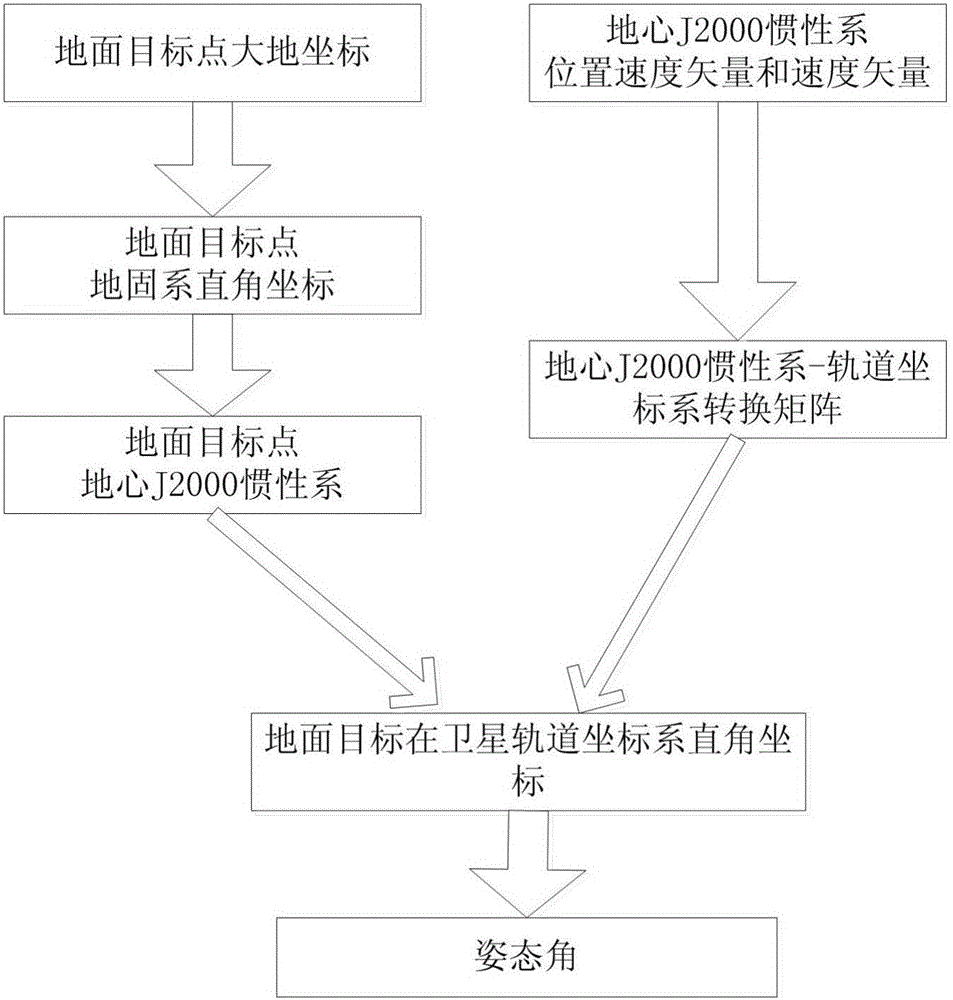
相比本发明的有益效果为：(1)基于空间几何关系给出航天器对地观测方程。该方法从几何观测出发，适应航天器两个姿态角可调节对地观测的需求。(2)航天器对地实时观测计算效率及精度高。(3)增长卫星的对地观测时间，实现卫星对地面目标的凝视效果。附图说明图1是卫星、地面目标和地球空间几何关系。图2是已知地面目标点位置卫星J2000系位置速度求卫星姿态角度步骤图。具体实施方式1用到的坐标系统和转换1.1坐标系的定义表1坐标系的定义1.2定义旋转矩阵在右旋直角坐标系中，以坐标轴的旋转而实现的坐标变换，可以通过旋转矩阵来表示新老坐标系之间的变换关系。定义如下三个旋转矩阵：Rx(θ)=1000cosθsinθ0-sinθcosθ]]>Ry(θ)=cosθ0-sinθ010sinθ0cosθ]]>Rz(θ)=cosθsinθ0-sinθcosθ0001]]>其中RK(θ)表示绕K轴正向旋转θ角(逆时针方向)。例，设新坐标系由原坐标系绕Z轴逆时针旋转θ角而得，则目标在新坐标系中的坐标(X’,Y’,Z’)与原坐标系中的坐标(X,Y,Z)存在如下关系：X′Y′Z′=RZ(θ)XYZ]]>1.3J2000.0惯性坐标系和地固坐标系之间的转换这两个坐标系之间的差别是极移、地球自转以及岁差章动。对于J2000.0惯性坐标系和地固系中的位置矢量rJ2000和rEG，有：rEG＝(EP)(ER)(NR)(PR)rJ2000(PR)为岁差矩阵，(NR)为章动矩阵，(ER)为地球自转矩阵，(EP)为极移矩阵。它们分别由下列各式表达：(EP)＝Ry(-xp)Rx(-yp)(ER)＝Rz(SG)(NR)＝Rx(-Δε)Ry(Δθ)Rz(-Δμ)(PR)＝Rz(-zA)Ry(θA)Rz(-ζA)各式中的xp,yp为极移分量，SG为格林尼治恒星时，ζA,θA,zA为岁差量，Δε,Δθ,Δμ为章动量。1.4大地坐标系与地固坐标系直角坐标的转换(X,Y,Z)为地固坐标系直角坐标；(B,L,H)为大地纬度、大地经度、大地高程；Re＝6378137m为地球赤道半径，ec为地球子午圈的偏心率。则X=(Re1-ec2sin2B+H)cosBcosLY=(Re1-ec2sin2B+H)cosBsinLZ=(Re1-ec2sin2B(1-ec2)+H)sinB]]>1.5J2000.0惯性坐标系和卫星轨道坐标系之间的转换记位置矢量从J2000.0惯性坐标系到卫星轨道坐标系的转换矩阵为C，由卫星轨道坐标系的定义可得转换矩阵C的各元素为：C(3,i)=-rJ2000rJ2000]]>C(2,i)=-rJ2000×r·J2000|rJ2000×r·J2000|]]>C(1,i)＝C(2,j)×C(3,k)其中：i＝1,2,3对应着转换矩阵C中每个行向量的三个分量。C(1,i),C(2,j),C(3,k)分别为矩阵C中第一行、第二行和第三行的行向量。1.6卫星轨道坐标系和卫星本体坐标系之间的转换在卫星轨道系中，定义绕X轴旋转为滚动角φ(也可称为侧摆)，定义绕Y轴旋转俯仰角θ，绕Z轴旋转偏航角：ψ，经坐标旋转到卫星本体系。根据旋转次序不同有个定义。1.7卫星本体坐标系和传感器基准坐标系之间的转换可认为卫星本体坐标系和传感器基准坐标系的坐标原点相同，转换关系可根据安装位置定义的通过坐标旋转得到。传感器安装于卫星本体系Z轴。2、已知地面目标点位置航天器J2000系位置速度求卫星姿态角度航天器、地面目标和地球空间几何关系如图1所示，已知地面目标点位置(大地坐标系下经度B、纬度L、高程H)，J2000坐标系下航天器某一时刻的位置速度矢量rJ2000和速度矢量步骤如下：1)将地面目标点在大地坐标系中的经度B、纬度L和高程H转换为地固坐标系中的直角坐标；2)将地面目标点在地固坐标系中的直角坐标转换为地心J2000惯性坐标系中的位置矢量robj；3)根据卫星在地心J2000坐标系中的位置速度矢量rJ2000和速度矢量求出地心J2000惯性坐标系到卫星轨道坐标系的转换矩阵；4)用转换矩阵C将地面目标点在地心J2000惯性坐标系中的位置矢量robj转换成卫星在轨道坐标系中的位置矢量r(x,y,z)；5)根据地面目标点在卫星轨道坐标系中的位置矢量r(x,y,z)求得卫星的姿态角，定义卫星绕X轴旋转时的姿态旋转角为横滚角绕Y轴旋转时的姿态旋转角为俯仰角θ，绕Z轴旋转时的姿态旋转角为偏航角ψ；卫星绕两个轴旋转，有以下四种方法可得到卫星的姿态角；方法1：卫星先绕Y轴旋转，再绕X轴旋转；由：得式中，(x,y,z)为地面目标点在卫星轨道坐标系中的位置矢量，r为位置矢量(x,y,z)的绝对值；方法2：卫星先绕X轴旋转，再绕Y轴旋转：由：得式中，(x,y,z)为地面目标点在卫星轨道坐标系中的位置矢量，r为位置矢量(x,y,z)的绝对值；方法3：卫星先绕Z轴旋转，再绕Y轴旋转：由xyz=sinθcosψsinθsinψcosθ]]>得式中，(x,y,z)为地面目标点在卫星轨道坐标系中的位置矢量，r为位置矢量(x,y,z)的绝对值；方法4：卫星先绕Z轴旋转，再绕X轴旋转：由得式中，(x,y,z)为地面目标点在卫星轨道坐标系中的位置矢量，r为位置矢量(x,y,z)的绝对值。完成基于地面目标点位置的卫星姿态角度的计算。现结合实施例、附图对本发明作进一步描述：已知地面目标点位置(大地坐标系下经度B、纬度L、高程H)，J2000坐标系下航天器某一时刻的位置速度矢量rJ2000和速度矢量按照图2的步骤计算出航天器的姿态角(φ,θ,ψ)。例：北京时2016年1月1日21：30航天器位置速度为/4406328.0，5117483.0，1311255.0，1699.0，448.0，-7406.0/若已知地面目标点坐标为(B＝10.0度L＝120.0度H＝0.0米)则计算出的四种转序的姿态角见表2。表2由地面点求出的四种转序的姿态角当前第1页1 2 3