一种基于位置和姿态测量系统的柔性杆臂测量方法与流程

本发明涉及一种基于位置和姿态测量系统的柔性杆臂测量方法，可用于测量载机存在挠曲变形时多载荷之间的柔性基线长度，提高多载荷之间相对的位置姿态精度。
背景技术：
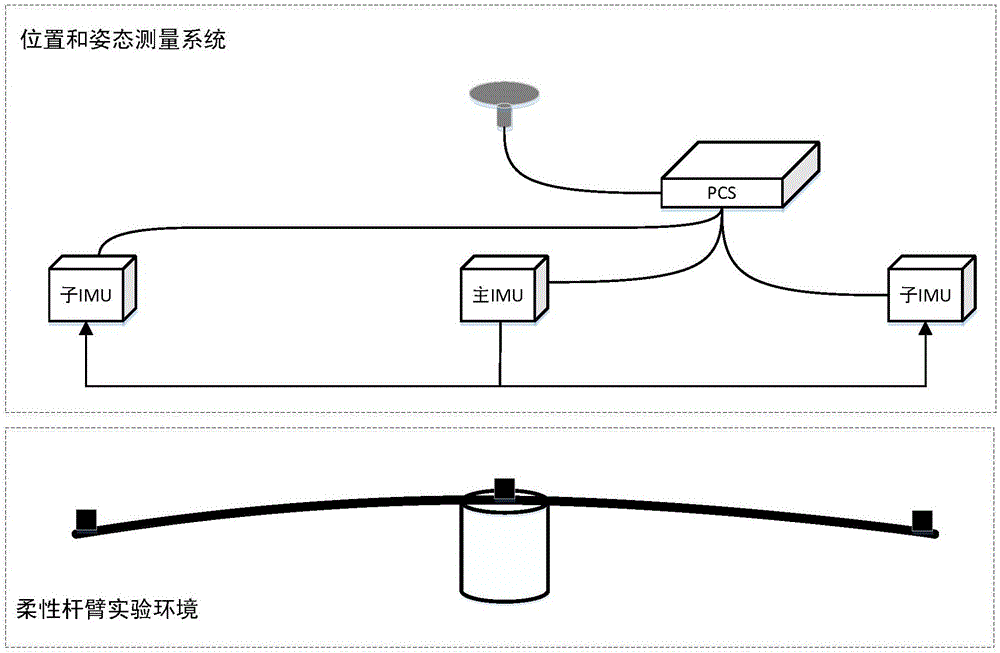
：高精度POS由惯性测量单元(InertialmeasurementUnit,IMU)、导航计算机系统(POSComputerSystem，PCS)和GPS组成。高精度POS可以为高分辨率航空遥感系统提供高频、高精度的时间、空间及精度信息，通过运动误差补偿提高成像精度和效率，是实现高分辨率成像的关键。我国在单POS成像方面取得了一定进展，但是由于对地观测载荷的需求牵引，如集成高分辨测绘相机、全谱段成像光谱仪、SAR于同一载体的多任务载荷，机载分布式阵列天线SAR和柔性多基线干涉SAR以及舰载稀疏阵列成像雷达等，多个或多种载荷安装在飞机不同位置，采用传统的单一POS系统无法实现多点的高精度位置姿态测量以及各载荷数据的时间统一。同时对于集成多个载荷的航空遥感系统和阵列载荷，由于飞机机体和柔性杆臂的挠曲变形、振动等因素，单个POS无法测量分布在飞机不同位置多个载荷的位置速度姿态信息。如果每个载荷都安装一个POS，不仅重量、成本增加，而且不同POS之间存在不同系统误差，使得多个载荷之间的数据难以融合，因此迫切需要建立高精度分布式时空基准系统，为高性能航空遥感系统中所有载荷提供高精度的时间、空间信息。现有的柔性杆臂测量方法(公开号：CN102322873)搭建了一种柔性杆臂测试环境并给出柔性杆臂测量精度验证方法，没有提供详细的柔性杆臂测量算法，没有解决动态条件下子IMU初始对准精度不高的问题，会直接限制子系统的位置姿态测量精度。针对柔性基线测量特性对测量精度要求较高的问题，在提高子IMU初始对准的姿态精度的同时，也要考虑子系统传递对准问题，提高整体系统的实时导航精度，实现柔性杆臂的精确测量。技术实现要素：本发明的技术解决问题是：克服现有技术的不足，提出了一种基于位置和姿态测量系统的柔性杆臂测量方法，克服传统初始对准方法动态条件下对准精度低的缺点，使得具有精度高、抗干扰能力强的特点，可用于测量载机存在挠曲变形时多载荷之间的柔性基线长度，提高多载荷之间相对的位置姿态精度。本发明技术解决方案是：一种基于位置和姿态测量系统的柔性杆臂测量方法，实现步骤如下：(1)首先搭建柔性杆臂的试验环境，将高精度主惯性测量单元(主IMU)及多个低精度子惯性测量单元(子IMU)安装在柔性杆臂结构架的对应安装节点上，系统上电；(2)然后高精度主惯性测量单元完成初始对准工作，并采用卡尔曼滤波方法估计出分布式POS主系统的位置、速度、姿态组合导航信息，完成主IMU组合导航；(3)同时低精度子惯性测量单元采用基于Rodrigues参数姿态描述的滤波方法进行动态基座下初始对准，估计出准确的姿态信息，完成子IMU初始对准；(4)最后，子IMU使用步骤(2)中主IMU高精度组合导航结果，进行传递对准，得到准确的子系统组合导航信息，解算出主/子IMU之间准确的基线长度，实现柔性杆臂测量。步骤(2)所述的卡尔曼滤波方法中状态变量X共有18维，包括东北天向的失准角东北天向的速度误差δVE、δVN、δVU，纬度、经度、高度误差δL、δλ、δH，x,y,z三个轴向的陀螺仪常值漂移误差εx、εy、εz，x,y,z三个轴向的加计常值漂移误差△x、△y、△z，x,y,z轴向杆臂长度误差△rx、△ry、△rz；量测量Z是经过杆臂补偿后的位置误差和速度误差，杆臂为GPS与主IMU之间的刚性杆臂。步骤(3)所述的基于Rodrigues参数姿态描述的滤波方法，利用姿态阵分解，将动态姿态的估计问题转化为一个常值姿态的估计，借助经典Rodrigues参数和姿态阵之间的凯莱变换，建立了在惯性坐标系内描述的二阶非线性的误差模型，采用非线性卡尔曼滤波算法完成更新，估计出较准确的姿态信息。步骤(4)所述的传递对准，利用主IMU精确的组合导航信息作为子IMU传递对准的基准，通过计算主IMU和子IMU直接的量测差反映子IMU的误差，同时将主IMU和子IMU之间的挠曲变形角作为状态变量建立挠曲变形模型，提高杆臂补偿精度，并借助“速度+姿态”的匹配方法实现杆臂修正，对挠曲变形的噪声进行积分平滑。“速度+姿态”的匹配方法实现如下：当量测量选用主、子惯性测量单元的速度误差和姿态误差进行传递对准时，量测值为主、子惯性测量单元的姿态角误差和速度误差，量测方程为Z＝HX+η，式中Z为量测变量，H为量测矩阵，η为量测噪声，Z＝[δψδθδγδVEδVNδVU]T其中δψ，δθ，δγ为系统的航向角误差、俯仰角误差、横滚角误差，即三个姿态误差，δVE,δVN,δVU为系统的东向、北向、天向速度误差，即三个速度误差。所述步骤(3)中子IMU初始对准采用基于Rodrigues参数姿态描述的滤波方法完成，具体步骤如下：实时姿态阵式中：nt系为实时导航坐标系，即载体时变位置东北天地理坐标系；in为导航惯性系，与动基座对准开始时刻的n系重合；b为载体坐标系；ib为载体惯性系，与对准开始时刻的b系重合。是运动的nt系相对于惯性系in的姿态阵，可由GPS输出位置信息解析计算；可利用陀螺输出进行姿态跟踪。因此，惯性系动基座对准的核心任务是对常值姿态阵的估计。利用牛顿第二定律和哥氏定理，经过简易推导可得到惯性系比力方程如下：vin·(t)+ωiein×vin(t)-gin(t)=fin(t)]]>式中：为t时刻载体对地速度在惯性系in内的投影；为t时刻载体所在位置重力加速度在in系内投影；为t时刻理想比力值。对式两端分别进行积分，并记∫0tk[vin·(τ)+(ωiein×vin(τ))-gin(τ)]dτ=Vrin(tk)]]>∫0tkfin(τ)dτ=Cibin∫0tkCbibfb(τ)dτ=CibinVmib(tk)]]>利用GPS输出可完成式中的求解式中：dVr1kin=∫tk-1tkvin·(t)dt=vin(tk)-vin(tk-1)]]>dVr2kin=∫tk-1tkvin(t)dt=∫tk-1tkCntinvnt(t)dt]]>dVr3kin=-∫tk-1tkgin(t)dt=-∫tk-1tkCntingnt(t)dt]]>进一步，在tk-1至tk更新周期内，假设为常矢量，导航系内对地速度为线性函数，即：Cntin=Cntk-1in[I+(t-tk-1)(ωinntk/k-1ntk/k-1)]]]>vnt(t)=vntk-1(tk-1)+vntk(tk)-vntk-1(tk-1)T(t-tk-1)]]>式中：t∈[tk-1,tk]；T＝tk-tk-1为GPS量测更新周期；整理可得：dVr2kin=Cntk-1in[IT2+T26(ωinntk/k-1ntk/k-1×)]vntk-1(tk-1)+Cntk-1in[IT2+T23(ωinntk/k-1ntk/k-1×)]vntk(tk)]]>dVr2kin=-Cntk-1in[IT+T22(ωinntk/k-1ntk/k-1×)]gntk|k-1]]>式中利用捷联惯导姿态、速度二子样更新算法，可以实现对上式中的求解。进一步，考虑陀螺仪随机常值漂移εb和加速度计随机常值零偏的影响，推导可得：Vmib^(tk)=Vmib(tk)+δVmib(tk)]]>δVmib·=Cbib^▿b+fib^×φib,δVmib(0)=0]]>φib·=-Cbib^ϵb,φib(0)=0]]>式中为姿态误差角；为加速度计惯性系比力积分误差。求解常值姿态阵的观测方程为：Vmib^(tk)-δVmib(tk)=CinibVrin(tk)]]>进一步，用经典Rodrigues参数法来等价描述姿态阵记对应Rodrigues参数为l，则二者满足凯莱变换关系式，即整理得：dtk=stk×l+l×δvm,tkib+ωv]]>式中ωv包含惯性器件测量噪声的积分和随机扰动的积分，且有综上，惯性系动基座对准可选取如下15维状态；X=lT(δVmib)T(φib)T(ϵb)T(▿b)TT]]>由上述推导，可得系统方程及量测方程分别为：l·δVmin·φib·ϵb·▿b·T=0000000fib^×0Cbib^000-Cbib^00000000000lδVminφibϵb▿b+0Cbib^ωa-Cbib^ωg00]]>dtk=h(Xk)+ωv=stk×l+(I+l×)δVmib+ωv]]>利用上式设计滤波算法，可以实现对l的估计，进而得到姿态阵即可实现动基座条件下的初始对准。本发明的原理是：首先搭建柔性杆臂的试验环境，将高精度主惯性测量单元(主IMU)及多个低精度子惯性测量单元(子IMU)安装在柔性杆臂结构架的对应安装节点上，系统上电。IMU进行初始对准，使用杆臂补偿后的GPS数据进行捷联组合解算，实现位置、速度、姿态信息的输出；子IMU结合主系统输出的组合导航信息，采用基于Rodrigues参数姿态描述的滤波方法进行初始对准；并采用基于“速度+姿态”的非线性滤波匹配方法，建立含挠曲杆臂误差的传递对准模型，借助主IMU位置速度信息姿态信息进行传递对准，获取子系统精确的位置、速度、姿态信息及主/子IMU之间的相对关系，实现柔性杆臂测量。本发明与现有技术相比的优点在于：本发明针对子IMU动态条件初始对准问题，采用基于Rodrigues参数姿态描述的滤波方法进行初始对准，克服传统初始对准方法对准精度低的缺点，提高了IMU初始姿态精度；将主/子IMU之间的挠曲变形误差作为状态变量建立挠曲变形模型，采用基于“位置+姿态”的传递对准方法得到较高精度的组合导航结果，克服传统惯性/卫星组合导航方法受杆臂变化影响大的不足，提高系统对柔性杆臂的测量精度。附图说明图1为本发明的系统数据处理流程图；图2为本发明的系统组成示意图；图3为本发明的基于Rodrigues参数姿态描述的滤波方法初始对准流程图；图4为本发明的传递对准流程图。具体实施方式如图1、2所示，本发明的具体实施步骤如下：1、将位置和姿态测量系统(POS)的惯性测量单元安装到柔性杆臂结构架的对应节点上，搭建实验环境。其中柔性杆臂结构架由柔性杆臂和稳定基座组成，柔性杆臂的正中央是主IMU安装节点，两端是子IMU安装节点，将柔性杆臂固定在稳定基座上，如图2所示。搭建实验需要的柔性杆臂环境，安装惯性测量单元，如图2所示，启动分布式POS测量系统进行测量。2、主IMU初始对准及组合导航(1)主IMU初始对准采用传统解析式方法完成：a、载体坐标系下：重力加速度g和地球自转角速度ωie可通过加速度计和陀螺仪的输出获得。b、导航坐标系下：当地的经度λ，纬度L可通过GPS数据获得，重力加速度g和地球自转角速度ωie在地理坐标系下的分量都是可以确定的，表示如下：gn=00gωien=ωiexnωieynωiezn=0ωiecosLωiesinL]]>c、捷联矩阵由下式求出：Cbn=(gn)T(ωien)T(gn×ωien)T-1(gb)T(ωieb)T(gb×ωieb)T]]>(2)主系统实时导航，包括捷联解算和卡尔曼滤波：a、捷联解算：以上一时刻的位置、速度、姿态作为作为当前捷联解算的初始值，结合当前时刻的主IMU数据，获得当前时刻的惯性导航结果。主要模块包括姿态矩阵更新、姿态计算、速度计算、位置矩阵更新和位置计算，说明如下：①姿态矩阵更新与姿态计算采用四元数法更新姿态矩阵Cnb=Tγ·Tθ·Tψ=cosγcosψ-sinγsinθsinψcosγsinψ+sinγsinθcosψ-sinγcosθ-cosθsinψcosθcosψsinθsinγcosψ+cosγsinθsinψsinγsinψ-cosγsinθcosψcosγcosθ]]>初始四元数计算公式为：q=q0q1q2q3=cosψ2cosθ2cosγ2-sinψ2sinθ2sinγ2cosψ2sinθ2cosγ2-sinψ2cosθ2sinγ2cosψ2cosθ2sinγ2+sinψ2sinθ2cosγ2cosψ2sinθ2sinγ2+sinψ2cosθ2cosγ2]]>即可由下式进行姿态更新计算：Cnb=q02+q12-q22-q322(q1q2-q0q3)2(q1q3+q0q2)2(q1q2+q0q3)q02-q12+q22-q322(q2q3-q0q1)2(q1q3-q0q2)2(q2q3+q0q1)q02-q12-q22+q32=T11T12T13T21T22T23T31T32T33]]>航向角ψ为IMU坐标系y轴在导航坐标系水平面(XY面)的投影与导航坐标系y轴的夹角，从导航坐标系y轴起算，“逆时针”为正，有效范围为[0°，360°]；俯仰角θ为IMU坐标系y轴与导航坐标系水平面(XY面)间的夹角，以载荷抬头为正，即IMU坐标系y轴矢量指向高于水平面为正，反之为负，有效范围为[-90°，90°]；横滚角γ定义为IMU右倾为正(以IMU坐标系y轴矢量指向为前，IMU坐标系x轴指向为右)，左倾为负，有效范围为[-180°，180°]。姿态更新后由下式计算结果：②速度计算由下式计算速度更新：Vxn·Vyn·Vzn·=aibxnaibynaibzn+02ωiezn+ωenzn-2(ωieyn+ωenyn)-2(ωiezn+ωenzn)02ωiexn+ωenxn2ωieyn+ωenyn-2(ωiexn+ωenxn)0VxnVynVzn-00g]]>式中为导航坐标系下沿x,y,z三个轴的速度增量，为载体坐标系相对惯性空间的加速度在x,y,z三个轴的投影，为导航坐标系下地球自传角速度沿x,y,z三个轴方向上的投影，由上式求出加速度泽③位置矩阵更新与位置计算由下列微分方程进行位置矩阵更新：Cne·=CneΩenn,Ωenn=0-ωenznωenynωenzn0-ωenxn-ωenynωenxn0]]>式中分别为导航坐标系下导航坐标系相对地球坐标系的转动角速率沿x,y,z三个轴方向的投影，采用一阶欧拉法进行位置矩阵更新，速发表达式为：Cne(t+T)=Cne(t)+TCne(t)Ωenn(t)]]>式中T为惯性导航系统采样周期。完成位置矩阵更新后，即可计算出导航位置参数，记有：L=sin-1(C33)λ=tan-1(C32C31)]]>高度H由于纯惯性导航系统的高度计算通道是发散的，要使用外界高度信息对捷联解算算法的高度通道进行阻尼。3、子IMU初始对准：利用子IMU数据和主系统数据，采用基于Rodrigues参数姿态描述的滤波方法进行初始对准，如图3所示，具体步骤如下：实时姿态阵式中：nt系为实时导航坐标系，即载体时变位置东北天地理坐标系；in为导航惯性系，与动基座对准开始时刻的n系重合；b为载体坐标系；ib为载体惯性系，与对准开始时刻的b系重合。是运动的nt系相对于惯性系in的姿态阵，可由GPS输出位置信息解析计算；可利用陀螺输出进行姿态跟踪。因此，惯性系动基座对准的核心任务是对常值姿态阵的估计。利用牛顿第二定律和哥氏定理，经过简易推导可得到惯性系比力方程如下：vin·(t)+ωiein×vin(t)-gin(t)=fin(t)]]>式中：为t时刻载体对地速度在惯性系in内的投影；为t时刻载体所在位置重力加速度在in系内投影；为t时刻理想比力值。对式两端分别进行积分，并记：∫0tk[vin·(τ)+(ωiein×vin(τ))-gin(τ)]dτ=Vrin(tk)]]>∫0tkfin(τ)dτ=Cibin∫0tkCbibfb(τ)dτ=CibinVmib(tk)]]>利用GPS输出可完成式中的求解式中：dVr1kin=∫tk-1tkvin·(t)dt=vin(tk)-vin(tk-1)]]>dVr2kin=∫tk-1tkvin(t)dt=∫tk-1tkCntinvnt(t)dt]]>dVr3kin=-∫tk-1tkgin(t)dt=-∫tk-1tkCntingnt(t)dt]]>进一步，在tk-1至tk更新周期内，假设为常矢量，导航系内对地速度为线性函数，即：Cntin=Cntk-1in[I+(t-tk-1)(ωinntk/k-1ntk/k-1)]]]>vnt(t)=vntk-1(tk-1)+vntk(tk)-vntk-1(tk-1)T(t-tk-1)]]>式中：t∈[tk-1,tk]；T＝tk-tk-1为GPS量测更新周期；整理可得：dVr2kin=Cntk-1in[IT2+T26(ωinntk/k-1ntk/k-1×)]vntk-1(tk-1)+Cntk-1in[IT2+T23(ωinntk/k-1ntk/k-1×)]vntk(tk)]]>dVr2kin=-Cntk-1in[IT+T22(ωinntk|k-1ntk|k-1×)]gntk|k-1]]>式中利用捷联惯导姿态、速度二子样更新算法，可以实现对上式中的求解。进一步，考虑陀螺仪随机常值漂移εb和加速度计随机常值零偏的影响，推导可得：Vmib^(tk)=Vmib(tk)+δVmib(tk)]]>δVmib·=Cbib^▿b+fib^×φib,δVmib(0)=0]]>φib·=-Cbib^ϵb,φib(0)=0]]>式中为姿态误差角；为加速度计惯性系比力积分误差。求解常值姿态阵的观测方程为：Vmib^(tk)-δVmib(tk)=CinibVrin(tk)]]>进一步，用经典Rodrigues参数法来等价描述姿态阵记对应Rodrigues参数为l，则二者满足凯莱变换关系式，即整理得：dtk=stk×l+l×δvm,tkib+ωv]]>式中ωv包含惯性器件测量噪声的积分和随机扰动的积分，且有综上，惯性系动基座对准可选取如下15维状态；X=lT(δVmib)T(φib)T(ϵb)T(▿b)TT]]>由上述推导，可得系统方程及量测方程分别为：l·δVmin·φib·ϵb·▿b·T=0000000fib^×0Cbib^000-Cbib^00000000000lδVminφibϵb▿b+0Cbib^ωa-Cbib^ωg00]]>dtk=h(Xk)+ωv=stk×l+(I+l×)δVmib+ωv]]>式中l为Rodrigues参数，包含三个速度误差，包含三个角度误差，εb包含三个陀螺仪常值漂移误差，包含三个加速度计常值漂移误差。利用上式设计滤波算法，可以实现对l的估计，进而得到姿态阵即可实现动基座条件下的初始对准。4、子系统建立含挠曲杆臂误差的传递对准模型，传递对准采用基于“速度+姿态”的非线性滤波匹配方法。其原理是利用主POS的高精度速度、姿态信息与子POS的速度、姿态信息之差对主、子POS间的姿态误差角进行估计并修正。滤波器的模型包括状态方程和量测方程。如图4所示，具体步骤如下：在考虑挠性杆臂误差的情况下，则量测方程可进一步描述为：y＝Hx0+v+fs其中fs为挠曲变形产生的量测误差，在此作为传感器小故障处理。下面简要分析fs的产生和传播机理。考虑主、子IMU之间的三轴挠曲变形角θ满足二阶马尔科夫过程的情况:θ··x+2βxθ·x+βx2θx=ηxθ··y+2βyθ·y+βy2θy=ηyθ··z+2βzθ·z+βz2θz=ηz]]>其中，τi为三轴挠曲变形过程的相关时间；ηi为白噪声，其方差为：为三个挠曲变形角的方差。主、子IMU的载体系之间的关系在小角度时可由如下方向余弦阵来确定：Cba=1-μzμyμz1-μz-μyμx1=I+μ×]]>式中：μx=ρx+θxμy=ρy+θyμz=ρz+θz]]>ρx、ρy、ρz和θx、θy、θz分别为子IMU相对主IMU的固定安装误差角和挠曲变形角在b系各个轴上的分量。主IMU导航系n和子IMU计算导航系n1之间的关系在小角度下可由如下方向余弦阵来确定：Cnn1=1φz-φy-φz1φxφy-φx1=1-φ×]]>其中，φ×为n1系相对n系的失准角φx、φy、φz组成的斜对称阵。进一步，根据传递对准的原理可得：Can=Ta,Cbn1=Cnn1CanCba=Tb]]>忽略二阶小量乘积，取近似值有：Tb＝Ta+Ta(μ×)-(φ×)Ta设主、子IMU计算出的航向角、俯仰角及横滚角分别为ψ、θ、γ和ψx、θy、γz。Ti=Ti(11)Ti(12)Ti(13)Ti(21)Ti(22)Ti(23)T(31)Ti(32)Ti(33),i=a,b]]>则有：tan(ψ+δψ)=-Ta(12)+Ta(22)φz-Ta(32)φy-Ta(11)μz+Ta(13)μxTa(22)-Ta(12)φz+Ta(32)φx-Ta(21)μz+Ta(23)μx]]>tan(γ+δγ)=-Ta(31)+Ta(11)φy-Ta(21)φx+Ta(32)μz-Ta(33)μyTa(33)+Ta(13)φy-Ta(23)φx+Ta(31)μy-Ta(32)μx]]>sin(θ+δθ)=Ta(32)+Ta(12)φy-Ta(22)φx-Ta(31)μz+Ta(33)μx]]>两边按泰勒级数展开，均取前两项并忽略二阶小量，整理得到：δψ=Ta(12)Ta(32)(Ta(12))2+(Ta(22))2φx+Ta(22)Ta(32)(Ta(12))2+(Ta(22))2φy-φz+Ta(12)Ta(23)-Ta(13)Ta(22)(Ta(12))2+(Ta(22))2μx+Ta(11)Ta(22)-Ta(12)Ta(21)(Ta(12))2+(Ta(22))2μz]]>δψ=-Ta(22)1-(Ta(32))2φx+Ta(12)1-(Ta(32))2φy-Ta(31)1-(Ta(32))2μz+Ta(33)1-(Ta(32))2μx]]>δγ=Ta(21)Ta(33)-Ta(31)Ta(23)(Ta(33))2+(Ta(31))2φx+Ta(31)Ta(13)-Ta(11)Ta(33)(Ta(33))2+(Ta(31))2φy-Ta(31)Ta(32)(Ta(33))2+(Ta(31))2μx+μy-Ta(32)Ta(33)(Ta(33))2+(Ta(31))2μz]]>综上，式中含有μi的项即为由于挠曲变形和固定安装误差角引起的量测误差fs，可知：fs=H2H303×303×3ρθ]]>其中，H2=H3=Ta(12)Ta(23)-Ta(13)Ta(22)(Ta(12))2+(Ta(22))20Ta(11)Ta(22)-Ta(12)Ta(21)(Ta(12))2+(Ta(22))2Ta(33)1-(Ta(32))20-Ta(31)1-(Ta(32))2-Ta(31)Ta(32)(Ta(33))2+(Ta(31))21-Ta(32)Ta(33)(Ta(33))2+(Ta(31))2]]>分析了量测误差fs的产生和传播机理后，进一步，为了准确地对其进行检测和补偿，必须将引起量测误差的fs的固定安装误差角与挠曲变形角纳入系统模型的状态变量之中，设计卡尔曼滤波器，对其估计。在此情况下，定义新的传递对准模型系统状态变量如下：x=φxφyφzδVxδVyδVzδLδλδhϵxϵyϵz▿x▿y▿zρxρyρzθxθyθzθ·xθ·yθ·zT]]>从而可以得到含挠性杆臂误差的传递对准模型为：x·=Fx+Gwy=Hx+v]]>其中，F=F1F2F3Cbn103×303×303×303×3F4F5F603×3Cbn103×303×303×303×3F7F803×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×303×3I3×303×303×303×303×303×303×3B1B2]]>B1=-βx2000-βy2000-βz2,B2=-2βx000-2βy000-2βz,G=Cbn103×303×303×3Cbn103×3015×3015×3015×303×303×3I3×3]]>H=H103×303×9H2H303×303×3I3×303×903×303×303×3]]>利用卡尔曼滤波估计的结果对系统状态变量进行反馈校正，得到子系统的组合导航结果，进而可以得到主IMU和子IMU之间准确的基线长度。当前第1页1 2 3