一种柔性磁悬浮轴承转子刚度阻尼辨识方法与流程

本发明公开了一种考虑干扰力影响的柔性磁悬浮轴承转子刚度阻尼辨识方法，属于磁悬浮轴承动态特性辨识
技术领域：
。
背景技术：
：磁悬浮轴承具有无需润滑、无摩擦、可以高速高效运行等优点。其已广泛应用于汽轮机，离心机和航空发动机等旋转机械设备中。准确的获得磁悬浮轴承的刚度阻尼数值，是磁悬浮轴承转子动力学计算的基础，包括临界转速计算、不平衡响应分析、模态振型计算、稳定性分析等。因此，磁悬浮轴承的刚度阻尼辨识具有重要意义。在本发明之前，磁悬浮轴承刚度阻尼的辨识理论和方法主要为发表在MechanicalSystemsandSignalProcessing期刊的基于刚性转子模型-响应面辨识方法(JinZhou,et.,Arotorunbalanceresponsebasedapproachtotheidentificationnoftheclosed-loopstiffnessanddampingcoefficientsofactivemagneticbearings,MechanicalSystemsandSignalProcessing,66(2016)665-678.)。上述方法只适用于无干扰力的理想条件下的刚性磁悬浮轴承转子模型，因此其存在两个缺点：(1)当转子自身残余不平衡量较大或者有电机干扰力等干扰存在时，磁悬浮轴承刚度阻尼辨识误差急剧增大；(2)当转子转速接近弯曲临界转速时，转子产生明显的弯曲变形，磁悬浮轴承刚度阻尼辨识误差急剧增大。技术实现要素：本发明所要解决的技术问题是针对上述
背景技术：
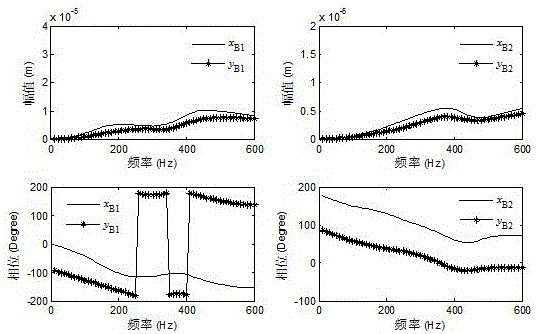
的不足，提供了一种考虑干扰力影响的柔性磁悬浮轴承转子刚度阻尼辨识方法，此方法可以考虑干扰力影响，且不仅适用于弯曲临界转速以下的刚性磁悬浮轴承转子，同时也适用于弯曲临界转速以上的柔性磁悬浮轴承转子刚度阻尼辨识，解决了现有的辨识方法存在的问题。本发明提供的一种柔性磁悬浮轴承转子刚度阻尼辨识方法包括如下步骤：步骤1：采用梁单元建立柔性转子数学模型；步骤2：在磁悬浮轴承转子系统的转子部位加入已知质量的不平衡质量，将磁悬浮轴承转子进行旋转运行，通过位移传感器采集不同转速下的磁悬浮轴承位移处的不平衡振动响应，同时采集转速信号；步骤3：在磁悬浮轴承转子系统的转子部位不加入任何不平衡质量，将磁悬浮轴承转子进行旋转运行，通过位移传感器采集不同转速下的磁悬浮轴承位移处的不平衡振动响应，同时采集转速信号；步骤4：将所述步骤2采集的数据，通过零相位滤波与一阶次傅里叶级数拟合，获得加入已知质量情况下的不平衡响应幅值数值；将拟合的一阶次傅里叶级数相位与转速相位做差，获得加入已知质量情况下的不平衡响应相位数据；步骤5：将所述步骤3采集的数据，通过零相位滤波与一阶次傅里叶级数拟合，获得不加入任何不平衡质量情况下的不平衡响应幅值数值；将拟合的一阶次傅里叶级数相位与转速相位做差，获得不加入任何不平衡质量情况下的不平衡响应相位数据；步骤6：用所述步骤4中获得不平衡响应减去步骤5获得的不平衡响应数值，获得幅值与相位数据即剔除干扰力之后的不平衡响应数值；步骤7：利用矩阵逆变换方法，将所述剔除干扰力的不平衡相应数值转换到磁悬浮轴承传感器节点处；利用所述磁悬浮轴承传感器节点处的不平衡激振力与步骤6得到的传感器节点处的不平衡响应数值，计算获得磁悬浮轴承的刚度与阻尼数值。所述步骤7的具体为：步骤7-1：建立加入不平衡质量的磁悬浮轴承动力学方程：MRq··+(CR+CB+ΩGR)q·+(KR+KB)q=funb+fres---(1)]]>上式(1)中MR为转子质量矩阵，CR为转子阻尼矩阵，KR为转子刚度矩阵，GR为转子陀螺矩阵，q为转子各个节点位移响应向量；CB，KB为磁悬浮轴承提供的支承阻尼数值，即所需要辨识参数；funb为加入不平衡质量的不平衡激振力；fres为干扰激振力；步骤7-2：建立不加入任何不平衡质量的磁悬浮轴承动力学方程：MRq··+(CR+CB+ΩGR)q·+(KR+KB)q=fres---(2)]]>步骤7-3：步骤7-1等式(1)减去步骤7-2等式(2)并进行拉氏变换：[(KR+KB-MRω2)+iω(CR+CB+ΩGR)]qm＝Funb(3)上式中，qm为节点位移响应向量之差；步骤7-4：将步骤7-3的等式(3)变化为传递函数形式，即：H＝[(KR+KB-MRω2)+iω(CR+CB+ΩGR)](4)步骤7-5：将步骤7-4的等式(4)拆分为转子自身传递函数HR与磁悬浮轴承提供刚度阻尼的传递函数HB：HR＝[(KR-MRω2)+iω(CR+ΩGR)](5)HB＝KB+iωCB.(6)步骤7-6：将步骤7-3的等式(3)用步骤7-5获得的等式(5)与(6)来表示：Hqm＝(HR+HB)qm＝Funb.(7)步骤7-7：将步骤7-6的等式(7)进行行列矩阵变换，此时需要将含有磁悬浮轴承两个传感器节点的平动位移向量，记为ZB1，ZB2变换到矩阵前两行；其余的节点位移向量记做ZO：H‾RZB1ZB2ZO+H‾BZB1ZB2ZO=00F‾unb---(8)]]>等式(8)中的为行列变换后的传递函数矩阵；步骤7-8：将步骤7-7中的与传递函数矩阵划分为3×3矩阵，表示为等式(9)：H‾R=HR11HR12HR13HR21HR22HR23HR31HR32HR33;H‾B=HB1000HB20000---(9)]]>此时HB1和HB2即为需要辨识的磁悬浮轴承位置处的传递函数矩阵，将其表示如下形式：HBi=Kxxi+iΩCxxi00Kyyi+iΩCyyi,i=1,2---(10)]]>步骤7-9：将步骤7-8的等式(9)带入步骤7-7的等式(8)中，获得等式(11):HR11HR12HR13HR21HR22HR23HR31HR32HR33ZB1ZB2ZO+HB1000HB20000ZB1ZB2ZO=00F‾unb.---(11)]]>由等式(11)的最后一行，得到等式(12)：ZO=HR33-1{F‾unb-HR31ZB1-HR3ZB2}---(12)]]>由等式(11)的前两行，得到等式(13)与(14)：HR1ZB1+HR1ZB2+HR1Zo＝-HB1ZB1；(13)HR21ZB1+HR22ZB2+HR23ZO＝-HB2ZB2(14)步骤7-10：定义转换到磁悬浮轴承节点的不平衡激振力为fB1和fB2：fB1＝-(HR11ZB1+HR12ZB2+HR13ZO)(15)fB2＝-(HR21ZB1+HR22ZB2+HR23Zo)(16)由于Zo在等式(12)中可以求出，所以等式(15)与等式(16)定义的转换到磁悬浮轴承节点的不平衡激振力fB1和fB2可以求出；步骤7-11：由步骤7-10和步骤7-9获得的结果，通过矩阵求逆运算，获得考虑干扰力下的两个磁悬浮轴承的提供的刚度与阻尼数值，即：HB1=Kxx1+iΩCxx00Kyy1+iΩCyy1=fB1ZB1-1---(17)]]>HB2=Kxx+iΩCxx200Kyy2+iΩCyy=fB2ZB2-1.---(18).]]>本发明采用以上技术方案与现有技术相比，具有以下技术效果：1、此辨识方法可以剔除干扰力影响，具体包括转子自身残余不平衡力的影响、电机干扰力的影响等。2、此辨识方法可以在磁悬浮轴承转子系统旋转时即正常运行的情况下进行辨识。3、此辨识方法不仅适用于临界转速以下的刚性磁悬浮轴承转子，同时也适用于临界转速以上的柔性磁悬浮轴转子承刚度阻尼辨识，解决了现有的辨识方法存在的问题。附图说明图1为磁悬浮轴承转子坐标系图；图2为磁悬浮轴承位置的转子自身的不平衡响应仿真数值；图3为磁悬浮轴承位置处转子不平衡响应仿真数值；图4为磁悬浮轴承相互垂直的x,y两个方向仿真刚度辨识的结果曲线图；图5为磁悬浮轴承相互垂直的x,y两个方向仿真阻尼辨识的结果曲线图；图6为转子不平衡质量加入位置说明图；图7为磁悬浮轴承位置的转子自身的不平衡响应试验数值；图8为磁悬浮轴承位置的转子自身的不平衡响应试验数值；图9为试验的左右两磁悬浮轴承相互垂直的x,y两个方向上刚度与阻尼辨识数值。具体实施方式本发明提供一种柔性磁悬浮轴承转子刚度阻尼辨识方法，为使本发明的目的，技术方案及效果更加清楚，明确，以及参照附图并举实例对本发明进一步详细说明。应当理解，此处所描述的具体实施仅用以解释本发明，并不用于限定本发明。本发明所涉及一种柔性磁悬浮轴承转子刚度阻尼辨识方法包括如下步骤：步骤1：采用梁单元建立柔性转子数学模型；步骤2：在磁悬浮轴承转子系统的转子部位加入已知质量的不平衡质量，将磁悬浮轴承转子进行旋转运行，通过位移传感器采集不同转速下的磁悬浮轴承位移处的不平衡振动响应，同时采集转速信号；步骤3：在磁悬浮轴承转子系统的转子部位不加入任何不平衡质量，将磁悬浮轴承转子进行旋转运行，通过位移传感器采集不同转速下的磁悬浮轴承位移处的不平衡振动响应，同时采集转速信号；步骤4：将所述步骤2采集的数据，通过零相位滤波与一阶次傅里叶级数拟合，获得加入已知质量情况下的不平衡响应幅值数值；将拟合的一阶次傅里叶级数相位与转速相位做差，获得加入已知质量情况下的不平衡响应相位数据；步骤5：将所述步骤3采集的数据，通过零相位滤波与一阶次傅里叶级数拟合，获得不加入任何不平衡质量情况下的不平衡响应幅值数值；将拟合的一阶次傅里叶级数相位与转速相位做差，获得不加入任何不平衡质量情况下的不平衡响应相位数据；步骤6：用所述步骤4中获得不平衡响应减去步骤5获得的不平衡响应数值，获得幅值与相位数据即剔除干扰力之后的不平衡响应数值；步骤7：利用矩阵逆变换方法，将所述剔除干扰力的不平衡相应数值转换到磁悬浮轴承传感器节点处；利用所述磁悬浮轴承传感器节点处的不平衡激振力与步骤6得到的传感器节点处的不平衡响应数值，计算获得磁悬浮轴承的刚度与阻尼数值。所述步骤7的具体为：步骤7-1：建立加入不平衡质量的磁悬浮轴承动力学方程：MRq··+(CR+CB+ΩGR)q·+(KR+KB)q=funb+fres---(1)]]>上式(1)中MR为转子质量矩阵，CR为转子阻尼矩阵，KR为转子刚度矩阵，GR为转子陀螺矩阵，q为转子各个节点位移响应向量；CB，KB为磁悬浮轴承提供的支承阻尼数值，即所需要辨识参数；funb为加入不平衡质量的不平衡激振力；fres为干扰激振力；步骤7-2：建立不加入任何不平衡质量的磁悬浮轴承动力学方程：MRq··+(CR+CB+ΩGR)q·+(KR+KB)q=fres---(2)]]>步骤7-3：步骤7-1等式(1)减去步骤7-2等式(2)并进行拉氏变换：[(KR+KB-MRω2)+iω(CR+CB+ΩGR)]qm＝Funb(3)上式中，qm为节点位移响应向量之差；步骤7-4：将步骤7-3的等式(3)变化为传递函数形式，即：H＝[(KR+KB-MRω2)+iω(CR+CB+ΩGR)](4)步骤7-5：将步骤7-4的等式(4)拆分为转子自身传递函数HR与磁悬浮轴承提供刚度阻尼的传递函数HB：HR＝[(KR-MRω2)+iω(CR+ΩGR)](5)HB＝KB+iωCB.(6)步骤7-6：将步骤7-3的等式(3)用步骤7-5获得的等式(5)与(6)来表示：Hqm＝(HR+HB)qm＝Funb.(7)步骤7-7：将步骤7-6的等式(7)进行行列矩阵变换，此时需要将含有磁悬浮轴承两个传感器节点的平动位移向量，记为ZB1，ZB2变换到矩阵前两行；其余的节点位移向量记做ZO：H‾RZB1ZB2ZO+H‾BZB1ZB2ZO=00F‾unb---(8)]]>等式(8)中的为行列变换后的传递函数矩阵；步骤7-8：将步骤7-7中的与传递函数矩阵划分为3×3矩阵，表示为等式(9)：H‾R=HR1HR12HR13HR21HR22HR23HR31HR3HR33;H‾B=HB1000HB20000---(9)]]>此时HB1和HB2即为需要辨识的磁悬浮轴承位置处的传递函数矩阵，将其表示如下形式：HBi=Kxxi+iΩCxxi00Kyyi+iΩCyyi,i=1,2---(10)]]>步骤7-9：将步骤7-8的等式(9)带入步骤7-7的等式(8)中，获得等式(11):HR11HR12HR13HR21HR22HR23HR31HR32HR33ZB1ZB2ZO+HB1000HB20000ZB1ZB2ZO=00F‾unb.---(11)]]>由等式(11)的最后一行，得到等式(12)：ZO=HR33-1{F‾unb-HR31ZB1-HR32ZB2}---(12)]]>由等式(11)的前两行，得到等式(13)与(14)：HR11ZB1+HR12ZB2+HR13ZO＝-HB1ZB1；(13)HR21ZB1+HR22ZB2+HR13Zo＝-HB2ZB2(14)步骤7-10：定义转换到磁悬浮轴承节点的不平衡激振力为fB1和fB2：fB1＝-(HR11ZB1+HR12ZB2+HR13Zo)(15)fB2＝-(HR21ZB1+HR22ZB2+HR23Zo)(16)由于Zo在等式(12)中可以求出，所以等式(15)与等式(16)定义的转换到磁悬浮轴承节点的不平衡激振力fB1和fB2可以求出；步骤7-11：由步骤7-10和步骤7-9获得的结果，通过矩阵求逆运算，获得考虑干扰力下的两个磁悬浮轴承的提供的刚度与阻尼数值，即：HB1=Kxx1+iΩCxx100Kyy1+iΩCyy1=fB1ZB1-1---(17)]]>HB2=Kxx2+iΩCxx200Kyy2+iΩCyy2=fB2ZB2-1.---(18).]]>实施方式1，仿真计算辨识：1.1采用Nelson-Timoshenko梁单元，图1为磁悬浮轴承转子坐标系图，共有左右两个磁悬浮轴承，每个磁悬浮轴承控制力分解为相互垂直的x,y两个方向。K与C分布代表刚度与阻尼，其下标表示刚度与阻尼的方向。根据图1转子坐标系建立柔性磁悬浮轴承转子模型；设定左右两磁悬浮轴承支承位置分别位于转子有限元模型的节点20与节点40处，如图6所示；假定两磁悬浮轴承提供的刚度与阻尼如表1所示。假定干扰力为转子自身的残余不平衡力，其所在节点位置及数值如表2所示；假定外加的不平衡质量所在节点位置及数值如表3所示。表1假定的磁悬浮轴承提供的刚度与阻尼数值表2假定的转子自身的残余不平衡量表3假定的外加不平衡质量1.2计算磁悬浮轴承转子在给定的刚度阻尼数值下，只考虑干扰力激励下的磁悬浮轴承位置处转子自身的不平衡响应数值，如图2所示；1.3计算磁悬浮轴承转子在给定的刚度阻尼数值下，考虑干扰力和外加不平衡质量共同激励下的磁悬浮轴承位置处转子自身的不平衡响应数值，如图3所示；1.4将所述步骤1.2计算的数据，通过零相位滤波与一阶次傅里叶级数拟合，获得只考虑干扰力激励下不平衡响应幅值数值；将拟合的一阶次傅里叶级数相位与转速相位做差，获得只考虑干扰力激励下不平衡响应相位数据；1.5将所述步骤1.3计算的数据，通过零相位滤波与一阶次傅里叶级数拟合，获得考虑干扰力和外加不平衡质量共同激励下不平衡响应幅值数值；将拟合的一阶次傅里叶级数相位与转速相位做差，获得考虑干扰力和外加不平衡质量共同激励下不平衡响应相位数据；1.6用所述步骤1.5中获得不平衡响应减去步骤1.4获得的不平衡响应数值，获得幅值与相位数据即剔除干扰力之后的不平衡响应数值；1.7将步骤1.5、1.6获得的两组试验数据，带入
发明内容中的步骤7提出的辨识方法进行计算。1.8图4为仿真辨识刚度的结果；图5为仿真辨识阻尼的结果。图中直线为假定磁悬浮轴承提供的刚度与阻尼数值，其值为表1所示。星号点数据为不同转速下辨识结果，可以发现即使有干扰力存在下，本法明提出的辨识方法可以准确辨识，即星号点数据与直线据吻合度很高。而如果不考虑干扰力的存在进行辨识，结果如图4图5中圆圈点数据所示，可以看出不考虑干扰力对辨识结果影响很大。实施方式2，试验辨识：2.1在磁悬浮轴承转子上加入不平衡质量，如图6所示；不平衡质量的具体信息如表所示；表4试验中外加的不平衡质量2.2运行磁悬浮轴承转子系统，从转速50Hz开始，每隔10Hz采集一次磁悬浮轴承处的位移数据；同时采集转子转速数据。2.3将采集的数据，通过零相位滤波与一阶次傅里叶级数拟合，拟合成如下公式：y＝a0+a1cos(xω)+b1sin(xω),(19)此时，振动的幅值A与相位数据可以通过以下公式获得,等式中为转速相位数值，此时获得的试验位移振动幅值和相位数据如图7所示；2.4去掉转子上加入的不平衡质量，运行磁悬浮轴承转子系统，从转速50Hz开始，每隔10Hz采集一次磁悬浮轴承处的位移数据；同时采集转子转速数据，将获得数据再次利用步骤2.3的方法进行处理，获得没有不平衡质量激励下，即只有干扰力激励下的磁悬浮轴承位置处位移幅与值相位数据，如图8所示。2.5将获得的两组试验数据，带入
发明内容中的步骤7提出的辨识方法进行计算。图9为试验辨识结果图。从图9中可以看出，转子在临界转速附近区域(480Hz)有明显的突变，准确的反应了柔性转子系统临界转速附近振动急剧增大的情况。这说明了此方法适合柔性磁悬浮轴承转子系统的刚度阻尼辨识；辨识方式适合弯曲临界转速以上的情况。当前第1页1 2 3