一种针对卫星弱信号的接收机无辅助式捕获方法与流程

本发明涉及卫星导航技术领域，尤其涉及一种针对卫星弱信号的接收机无辅助式捕获方法。

背景技术：

当前，各行业对全球卫星导航系统的应用和依赖程度越来越高，相对于在野外开阔地域的定位服务，在密集城市环境中的定位、手机/车辆导航和室内外无缝定位等对卫星导航接收机的弱信号工作能力提出了更加苛刻的要求。

双块补零算法(DBZP,Double Block Zero Padding)是无辅助式弱信号捕获中得到广泛认可的一种捕获方法，能同时对多普勒频移和码相位进行并行搜索，是一种双频域搜索方法，非常适用于需要处理大量数据的弱信号捕获。但双块补零算法所需的运算量较大，需要占用定位设备较多的计算资源，为了保证运算时间和定位信号的刷新频率在可接收的范围内，需要定位设备配置足够的运算机能，比如更高性能的处理器、接收天线等，同时为了保证续航需要，还需提高定位设备的电池容量，这都造成了采用双块补零算法的定位设备存在成本较高的问题，难以同时兼顾定位性能和成本。

技术实现要素：

本发明的实施例提供一种针对卫星弱信号的接收机无辅助式捕获方法，能够减少运算量和运算时间，缓减定位设备同时兼顾定位性能和成本的问题。

为达到上述目的，本发明的实施例采用如下技术方案：

将接收到的基带信号分成N_b个块，并生成长度为T_I的测距码，将所述测距码分成N_b个块，其中，所述基带信号的长度为T_I，每个块包含S_b个采样点，所述测距码分成的每个块包含S_b个采样点；

将由所述基带信号分成的相邻的两个块组合，并将组合后的所述基带信号的每个块，分为指定数量的长度相等的子块，其中，组合后的所述基带信号的块表示为D＝[d(1) d(2) … d(N)]，其中包含2S_b个采样点，N＝S_b，由组合后的所述基带信号的每个块所划分出的子块具有相同数量的采样点；

将由所述测距码分成的每个块补上相同长度的零，并将补零后的所述测距码的每个块，分为所述指定数量的长度相等的子块，其中，补零后的块表示为每个块中所补零的个数为N/2，补零后的每个块含2S_b个采样点，由补零后的所述测距码的每个块所划分出的子块具有相同数量的采样点和零；

对所述基带信号和所述测距码的子块分别执行傅里叶变换(FFT)和反傅里叶变换(IFFT)，得到时域内的相干积分矩阵M_c；

得到M_c所有的点的能量，若所得能量的最大值大于捕获阈值，则捕获成功。

本发明实施例提供的针对卫星弱信号的接收机无辅助式捕获方法，对现有的双块补零(DBZP，Double Block Zero Padding)方法进行了改进和优化。针对块内运算傅里叶变换后有一半的运算结果是没有意义，浪费运算量的情况，对参与块内计算的基带信号和本地测距码进行了重构，降低了参与傅里叶变换的点数，使得傅里叶变换后无意义的运算结果降低了一半，在信噪比和检测概率不受影响的情况下，相对于现有的双块补零方法，减少了运算量和运算时间，从而缓减了定位设备同时兼顾定位性能和成本的问题。

附图说明

为了更清楚地说明本发明实施例中的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其它的附图。

图1为本发明实施例提供的针对卫星弱信号的接收机无辅助式捕获方法的流程图；

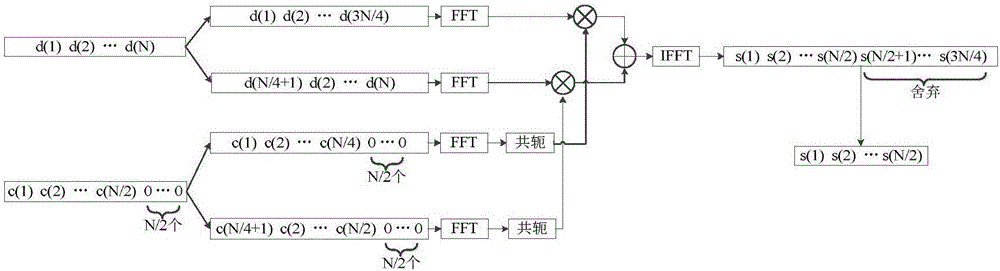
图2为本发明实施例提供的块内运算的逻辑流程图。

具体实施方式

为使本领域技术人员更好地理解本发明的技术方案，下面结合附图和具体实施方式对本发明作进一步详细描述。下文中将详细描述本发明的实施方式，所述实施方式的示例在附图中示出，其中自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。下面通过参考附图描述的实施方式是示例性的，仅用于解释本发明，而不能解释为对本发明的限制。本技术领域技术人员可以理解，除非特意声明，这里使用的单数形式“一”、“一个”、“所述”和“该”也可包括复数形式。应该进一步理解的是，本发明的说明书中使用的措辞“包括”是指存在所述特征、整数、步骤、操作、元件和/或组件，但是并不排除存在或添加一个或多个其他特征、整数、步骤、操作、元件、组件和/或它们的组。应该理解，当我们称元件被“连接”或“耦接”到另一元件时，它可以直接连接或耦接到其他元件，或者也可以存在中间元件。此外，这里使用的“连接”或“耦接”可以包括无线连接或耦接。这里使用的措辞“和/或”包括一个或更多个相关联的列出项的任一单元和全部组合。本技术领域技术人员可以理解，除非另外定义，这里使用的所有术语(包括技术术语和科学术语)具有与本发明所属领域中的普通技术人员的一般理解相同的意义。还应该理解的是，诸如通用字典中定义的那些术语应该被理解为具有与现有技术的上下文中的意义一致的意义，并且除非像这里一样定义，不会用理想化或过于正式的含义来解释。

本发明实施例提供一种针对卫星弱信号的接收机无辅助式捕获方法，如图1所示，包括：

S1、将接收到的基带信号分成N_b个块，并生成长度为T_I的测距码，将所述测距码分成N_b个块。

其中，所述基带信号的长度为T_I，每个块包含S_b个采样点，所述测距码分成的每个块包含S_b个采样点。

S2、将由所述基带信号分成的相邻的两个块组合，并将组合后的所述基带信号的每个块，分为指定数量的长度相等的子块。

其中，组合后的所述基带信号的块表示为D＝[d(1) d(2) … d(N)]，其中包含2S_b个采样点，N＝S_b，由组合后的所述基带信号的每个块所划分出的子块具有相同数量的采样点。

在本实施例的优选方案中，所述指定数量大于等于2。

例如：所述将组合后的所述基带信号的每个块，分为指定数量的长度相等的子块，其具体实现方式包括：将组合后的所述基带信号的每个块，分为两个长度均为3N/4个采样点的子块，其中，第一个子块表示为第二个子块表示为所述第一个子块包含所述组合后的所述基带信号的块的前面3/4个采样点，所述第二个子块包含所述组合后的所述基带信号的块的后3/4个采样点。

S3、将由所述测距码分成的每个块补上相同长度的零，并将补零后的所述测距码的每个块，分为所述指定数量的长度相等的子块。

其中，补零后的块表示为每个块中所补零的个数为N/2，补零后的每个块含2S_b个采样点，由补零后的所述测距码的每个块所划分出的子块具有相同数量的采样点和零。

例如：所述将补零后的所述测距码的每个块，分为指定数量的长度相等的子块，其具体实现方式包括：将补零后的所述测距码的每个块，分为长度为3N/4个采样点的子块，其中一个块表示为包含前N/4个测距码的采样点和N/2个零，另一个块表示为包含后N/4个测距码采样点和N/2个零。

S4、对所述基带信号和所述测距码的子块分别执行傅里叶变换(FFT)和反傅里叶变换(IFFT)，得到时域内的相干积分矩阵M_c。

其中，通过步骤S4得到时域内的相干积分矩阵M_c的过程也可称为“块内运算”，“块内运算”的具体实现过程包括：如图2所示的，分别得到所述基带信号和所述测距码的子块执行傅里叶变换后的结果。

本实施例中，S4的具体实现方式包括：

向分别得到所述基带信号和所述测距码的子块执行傅里叶变换后的结果；

并将所述测距码的子块执行傅里叶变换后的结果取共轭，到两组各包括3N/4个测距码采样点的数据；再将两组各包括3N/4个测距码采样点的数据相加，并进行反傅里叶变换(IFFT)，对于反傅里叶变换的结果保留前N/2个采样点，后N/4个采样点舍弃。例如：将所述测距码的子块执行傅里叶变换后的结果取共轭，然后C₁对应D₁，C₂对应D₂，分别点对点进行相乘，得到两组3N/4点数据。两组数据相加之后进行反傅里叶变换(IFFT)，得到变换后的数据保留前N/2个采样点，后N/4个采样点舍弃。所有块均进行上述操作，共得到N_b×S_b个采样点。这N_b×S_b个采样点构成相干积分矩阵M_c中前S_b列。上述只是执行了一次块内运算，测距码和基带信号需要进行遍历，即块1对块2，块2对块3…，第三次块内运算是块1对块3，块2对块4，直至循环到测距码完成一个周期，从而对所述基带信号和所述测距码的子块。进行了双块结合，得到若干个测距码的块和同等数量的基带信号的块，一个测距码块对应一个基带信号块执行块内操作，即块1对块1，块2对块2，等。然后块内执行重构运算后会各得到两个子块，即C₁C₂和D₁D₂，这其实是四组信号，然后C₁C₂先进行傅里叶变换再取共轭，D₁D₂只进行傅里叶变换，之后四组信号C₁对应D₁，C₂对应D₂进行点对点的相乘，得到两组信号，两组信号相加再进行IFFT。在实际应用中，该S4的具体实现方式可以在频域搜索的过程中执行

对所述基带信号和所述测距码的所有子块重复上述过程，再根据所有子块重复上述过程后的处理结果进行移块操作，得到M_c。

其中，所述根据所有子块重复上述过程后的处理结果进行“移块操作”，得到M_c，具体包括：所有子块重复上述过程后的基带信号统一左移1个块，再进行“块内运算”，得到M_c中对应的共计S_b列；对所有子块重复上述过程后的基带信号共移动(N_ms-1)次，将得到的所有列组成N_b×N_s的相干积分矩阵M_c。

由于双块补零算法的块内运算是经典的基于傅里叶变换的并行码相位捕获。频域内的并行码相位搜索等价于时域内测距码相对于信号依次向右移位后相应点成绩结果的累加，因此测距码的移位构成一个N×N的圆周相关矩阵C_N×N，其中N是块内的数据点数。本实施例中所提出的对与块内数据进行重构的“块内运算”，在上述圆周相关矩阵的基础上进行了简化。其中，假设块内基带信号序列和测距码序列分别为D(n)和C(n)，并行码相位搜索后的相关结果为S(n)，离散傅里叶变换的实现方程为：其中：D＝[d(1) d(2) … d(N)]；S＝[s(1) s(2) … s(N)]。

展开成时域矩阵的形式为：

S_N×1＝C_N×N×D_N×1

其中，为上述定义的N×N的圆周相关矩阵C_N×N，由于在本实施例中，并行码相位搜索的结果只保留前半部分，即所以矩阵C_N×N后面行的操作都是会被舍弃的。

在本实施例中的“块内运算”中先将C_N×N相应简化为：

展开成的时域矩阵简化为：

$S_{\frac{N}{2}\×1}=C_{\frac{N}{2}\×N}\×D_{N\×1}$

由于C_N×N简化为后，圆周相关矩阵丧失了原有的圆周相关性，无法进行离散傅里叶变换，因此需要重构矩阵的圆周相关性。在重构矩阵的圆周相关性之前，先对矩阵进行第二次简化，具体为将展开成两个“等价”矩阵相加的形式，其中第一个矩阵只保留的值，其它值全部置零，第二个矩阵对应的只保留的值，其它值全部置零。

从而得到：其中，在和中，都有列是全零的，分别是的第列至第列和最后一列，的第1列至第列和最后一列。分别将上述全零列删除，和简化为的矩阵和基带信号D(n)中对应的值也进行删除。

简化为

$S_{\frac{N}{2}\×1}=C_{\frac{N}{2}\×(\frac{3N}{4}-1),1}\×D_{(\frac{3N}{4}-1),1}+C_{\frac{N}{2}\×(\frac{3N}{4}-1),2}\×D_{(\frac{3N}{4}-1),2}$

重构矩阵圆周相关性，对和两个矩阵最后一行数据继续执行右移，分别增加行数据后，新生成的阶矩阵和具有圆周相关性。

其中，和分别是要保留和舍弃的部分。转换为基于傅里叶变换的时频域公式为：

其中，至此实现了“块内运算”，且在保证原始输入序列不变，有效运算不变的情况下，参与离散傅里叶变换的数据点长度由N下降到

上述通过“块内运算”进行块内重构的方法适用于基于双块补零的弱信号检测和捕获，除了适合于卫星导航接收机的应用，同样的思想适用于其它CDMA信号体制的信号捕获。

S5、得到M_c所有的点的能量，若所得能量的最大值大于捕获阈值，则捕获成功。

其中，在得到时域内的M_c矩阵后，对M_c的每一列进行离散傅里叶变换。算出此矩阵所有的点的能量，如果最大值大于给出的捕获阈值，那么捕获成功。如果矩阵内的最大值小于给出的捕获阈值，则可进行非相关积分以增加信号的后处理信噪比。

在本实施例中，对基带信号和测距码均进行了重构，重构之后所得子块的采样点数由N降低为3N/4。从而降低了参与FFT的点数。基于本实施例的设计思路，还可以通过对基带信号和测距码进行重构，并将原来的块分为更多的子块，从而进一步降低参与FFT的点数。

虽然重构之后所得子块的采样点数由N降低为3N/4，且重组成两个长度为的离散傅里叶变换，虽然参与傅里叶变化的序列长度变短了，但是傅里叶变换的次数由一次增加到了两次。而在实际的工程实现中，FFT的实现的前提是参与傅里叶变换的点数是2的整数幂，即基-2FFT。基-2FFT算法在DSP/FPGA等可编程器件中已经得到了充分的实现，如果参与FFT的点数不是2的整数幂，就需要通过补零的操作达到2的整数幂，过多的补零操作不仅会增加计算量，还会导致信号的损失，尤其对于卫星弱信号的监测和捕获，是非常不利的。在码相位未知的情况下，如果本地复制信号与接收信号补零的位置不一致时，将降低测距码自相关峰值，严重时如果补零的位置相差半个测距码周期，则自相关峰值将减半。例如：假设原始参与块内运算的数据长度为600，则基-2FFT下需要将数据长度补零扩充至1024(210)，但是通过块内重构，参与傅里叶变换的点数降低到450，则基-2FFT下只需要将数据长度补零至512(29)，FFT的点数降低了一半。因此通过微调多普勒的搜索范围或采样频率等，我们可以达到重构后的FFT点数为原始点数一半的理想情况。

基-2FFT所需要的乘法操作数为现有双块补零算法所需要的乘法操作数为块内重构之后的算法所需要的乘法操作数为在理想情况下有所以块内重构后的算法的乘法操作数为

当运算点数为512时，本实施例改进的“块内运算”算法相比现有双块补零算法理论上可以减少25％的运算量。而随着FFT点数的增加，改进的“块内运算”算法相比现有双块补零算法的减少量所占比重会降低，这是由于改进的“块内运算”算法有两次FFT运算导致的，但是通过现有双块补零算法则参与块内运算的点数不会过大，因此本实施例所能够减少的运算量非常明显。

本发明实施例提供的针对卫星弱信号的接收机无辅助式捕获方法，对现有的双块补零(DBZP，Double Block Zero Padding)方法进行了改进和优化。针对块内运算傅里叶变换后有一半的运算结果是没有意义，浪费运算量的情况，对参与块内计算的基带信号和本地测距码进行了重构，降低了参与傅里叶变换的点数，使得傅里叶变换后无意义的运算结果降低了一半，在信噪比和检测概率不受影响的情况下，相对于现有的双块补零方法，减少了运算量和运算时间，从而缓减了定位设备同时兼顾定位性能和成本的问题。

并且，目前大多数的对基于双块补零算法的弱信号捕获的改进方案，主要是对比特跳变的检测方式的优化，实质上是对块内运算之后得到的相干积分矩阵进行各种不同数据位的组合的方法进行优化，以达到降低运算量的目的。而本发明实施例则针对块内运算进行优化，对参与块内运算的基带信号和本地测距码进行重构，降低了参与傅里叶变换的点数，达到降低计算量，提高运行速度的目的，技术相对简单、易于实现，具有较强的工程应用价值，尤其适用于以较低成本对卫星导航接收机的改进。

本说明书中的各个实施例均采用递进的方式描述，各个实施例之间相同相似的部分互相参见即可，每个实施例重点说明的都是与其他实施例的不同之处。尤其，对于设备实施例而言，由于其基本相似于方法实施例，所以描述得比较简单，相关之处参见方法实施例的部分说明即可。以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到的变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应该以权利要求的保护范围为准。