一种偏振干涉光谱复原的修正方法与流程

本发明涉及傅里叶变换光谱复原领域，特别是一种偏振干涉光谱复原的修正方法。

背景技术：

对于经典的迈克尔逊干涉光谱仪而言，动反射镜在扫描时任意波长的光程差变化在理论上讲是一致的。任意波长的余弦干涉曲线的相位变化主要取决于波数和扫描量，不同波长的调制频率之比等于波数之比。因此，对于复色光，直接进行快速傅里叶变换(Fast fourier transform，FFT)即可准确还原出光谱曲线。对于一些非线性干涉信号比如弹光调制干涉，其相位变化与扫描量呈非线性关系，而傅里叶变换只适用于相位均匀采样的前提下，因此直接用FFT将带来严重的光谱失真，于是一种非均匀快速傅里叶变换(Non-uniform fast fourier transform，NUFFT)算法应运而生，该算法在论文“弹光调制干涉具干涉数据的获取及光谱复原”(激光技术,2013,37(3):409-412.)中作了详细报道。

对于偏振干涉而言，干涉曲线的相位变化与上述两种形式均有不同。首先，对单波长而言，相位变化与扫描量是线性的，这一点与经典迈克尔逊干涉是一致的，因此无法采用NUFFT算法；其次，不同波长的调制频率之比则取决于波数与双折射率差的乘积，因此不能直接采用FFT，否则将导致严重的光谱失真。综上所述，对于偏振干涉光谱而言，传统的FFT和NUFFT均无法准确进行光谱复原。

技术实现要素：

为了解决背景技术中所存在的技术问题，本发明提出了一种偏振干涉光谱复原的修正方法，在FFT的基础上对所得波数按照晶体材料的色散特性进行逐一补偿和修正，最终获得准确的光谱复原。

本发明的技术方案是：一种偏振干涉光谱复原的修正方法，其特 殊之处在于：包括以下步骤：

1】预处理

所述预处理包括干涉信号采样、降噪和相位校正；确定快速傅里叶变换(Fast fourier transform，FFT)点数N；确定波数范围v₀～v₁；

2】傅里叶变换

对预处理所得干涉信号采用FFT算法进行计算，得到波数v′₁与波数v′₀；

3】修正

单色光的偏振干涉曲线调制频率随着扫描保持稳定，不同波长的干涉曲线调制频率之比为双折射率差与实际波数乘积之比；设定光谱范围中最高波数v₀为基准：

$\frac{f_1}{f_0}=\frac{{\mathrm{\Δn}}_1{v}_1}{{\mathrm{\Δn}}_0{v}_0}=\frac{v_1^{\′}}{v_0^{\′}}---\left(3\right)$

利用FFT所得波数v′₁、v′₀和基准波数v₀之间的数学关系如公式(3)，采用牛顿法求解出真实的波数v₁，从而完成波数的修正；经过上述步骤将v₀～v₁范围内所有波数v_n逐一修正；

4】坐标变换

将修正后的波数v_n与FFT所得的幅值建立对应关系，得到修正后光谱曲线；

上述步骤2】傅里叶变换获得初始波数值；所述步骤3】修正获得修正后的真实波数值。

上述步骤3】修正方法中所用的不同波长双折射率差值取决于晶体材料的色散方程，具体公式如下：

${n_o}^2=2.6926+\frac{0.0192}{{\mathrm{\λ}}^2-0.0195}-0.0143{\mathrm{\λ}}^2---\left(4\right)$

${n_e}^2=2.1846+\frac{0.0085}{{\mathrm{\λ}}^2-0.0143}-0.0023{\mathrm{\λ}}^2---\left(5\right)$

Δn＝n_o-n_e (6)

其中：f₁、f₂调制频率；

Δn1和Δn0晶体材料的双折射率差；

v0、v1、vn为修正后的波数；

v′₀、v′₁为FFT后所得的波数；

λ为波长。

本发明的技术优点是：采用直接FFT结合波数修正相结合的方法，实现偏振干涉信号的光谱复原。采用FFT算法具有算法成熟、快速和准确的优点，结合波数修正只需确定相位补偿器的材料属性即可采用软件算法的方式进快速、有效地将FFT所得波数逐一补偿。

附图说明

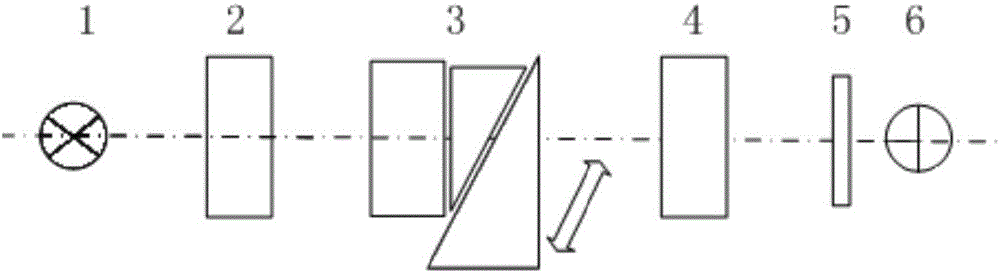
图1为偏振干涉仪光路图；

图2为未经修正的双波长光谱复原图；

图3为修正后的双波长光谱复原图。

其中，1－准直光源，2－起偏器，3－相位补偿器，4－检偏器，5－滤波片，6－探测器。

具体实施方式

偏振干涉仪双折射晶体为相位补偿器件，参与干涉的两束光共光路，与传统的迈克尔逊等双支路干涉仪相比，不存在光束的分合，具有天然的不失调性和优良的抗干扰能力，在在线分析中具有广阔的应用前景。

本发明提出一种偏振干涉光谱复原的修正方法，包括以下步骤：

1】预处理

所述预处理包括干涉信号采样、降噪和相位校正；确定快速傅里叶变换(Fast fourier transform，FFT)点数N；确定波数范围v₀～v₁；

2】傅里叶变换

对预处理所得干涉信号采用FFT算法进行计算，得到波数v′₁与波数v′₀；

3】修正

单色光的偏振干涉曲线调制频率随着扫描保持稳定，不同波长的干涉曲线调制频率之比为双折射率差与实际波数乘积之比；设定光谱范围中最高波数v₀为基准：

$\frac{f_1}{f_0}=\frac{{\mathrm{\Δn}}_1{v}_1}{{\mathrm{\Δn}}_0{v}_0}=\frac{v_1^{\′}}{v_0^{\′}}---\left(3\right)$

利用FFT所得波数v′₁、v′₀和基准波数v₀之间的数学关系如公式(3)，采用牛顿法求解出真实的波数v₁，从而完成波数的修正；经过上述步骤将v₀～v₁范围内所有波数v_n逐一修正；

4】坐标变换

将修正后的波数v_n与FFT所得的幅值建立对应关系，得到修正后光谱曲线；

步骤2】傅里叶变换获得初始波数值；所述步骤3】修正获得修正后的真实波数值。

步骤3】修正方法中所用的不同波长双折射率差值取决于晶体材料的色散方程，具体公式如下：

${n_o}^2=2.6926+\frac{0.0192}{{\mathrm{\λ}}^2-0.0195}-0.0143{\mathrm{\λ}}^2---\left(4\right)$

${n_e}^2=2.1846+\frac{0.0085}{{\mathrm{\λ}}^2-0.0143}-0.0023{\mathrm{\λ}}^2---\left(5\right)$

Δn＝n_o-n_e (6)

其中：f₁、f₂调制频率；

Δn1和Δn0晶体材料的双折射率差；

v0、v1、vn为修正后的波数；

v′₀、v′₁为FFT后所得的波数；

λ为波长。

如图1，偏振干涉仪的工作原理如下：

准直光源1为自然光，经起偏器起偏后转换成为线偏振光，偏振光经相位补偿器3后分成两束传播方向一致，振动方向相互垂直，且具有一定相位差的线偏振光，两线偏振光中与检偏器4透光轴方向一 致的投影分量将被透射。透射后两透射分量光频率相同、振动方向相同且具有固定的相位差，因此满足干涉条件。干涉光经滤波片5后由探测器6接收。当相位补偿器3内部的扫描光楔沿其斜边做一维直线运动时，两束偏振分量之间的相位差将连续改变，因此探测器6所得到的光电信号将随时间起伏。对于单色光，干涉信号去直流成分后干涉光强

I＝B(v)[cos2πx(n_o-n_e)v] (1)

式中v为波数，B(v)为某一波数的光强度，x为相位补偿器的量，Δn＝n_o-n_e为相位补偿器所用晶体材料的双折射率差。对于宽光谱光源，探测器6所得干涉信号为各单色光干涉信号的线性叠加，即有

$I=\underset{{\mathrm{\υ}}_1}{\overset{{\mathrm{\υ}}_2}{\Σ}}B\left(v\right)\[cos2\mathrm{\π}x(n_o-n_e)v\]---\left(2\right)$

对于波数为v0，v1的单色光，其干涉曲线的调制频率之比为

$\frac{f_1}{f_0}=\frac{{\mathrm{\Δn}}_1{v}_1}{{\mathrm{\Δn}}_0{v}_0}=\frac{v_1^{\′}}{v_0^{\′}}---\left(3\right)$

其中Δn₁和Δn₀分别为v₀和v₁对应的双折射率差，并且Δn₁和Δn₀分别是v₀和v₁的函数。假设相位补偿器的晶体材料为冰洲石(Calcite)，该材料是一种色散材料，不同波长的单色光对应的o光和e光折射率n_o和n_e都不一样。根据Sellmerier色散方程：

${n_o}^2=2.6926+\frac{0.0192}{{\mathrm{\λ}}^2-0.0195}-0.0143{\mathrm{\λ}}^2---\left(4\right)$

${n_e}^2=2.1846+\frac{0.0085}{{\mathrm{\λ}}^2-0.0143}-0.0023{\mathrm{\λ}}^2---\left(5\right)$

Δn＝n_o-n_e (6)

λυ＝10000 (7)

根据上式可以求解出冰洲石在透射光谱范围内任意波长的no和ne，且no和ne均为波数的方程。在扫描过程中不同波长的余弦干涉频率是不一样的，而同一波长的调制频率在扫描过程中则始终保持稳 定。

对于迈克尔逊干涉而言，因不存在双折射，故Δn1和Δn0之比等于1，因此直接FFT所得的频率值即是真实的波数。对于偏振干涉而言，Δn1和Δn0存在微小的差异，因此直接FFT将不再适用，必须对波数修正。其方法如下：

对干涉数据进行采样、降噪和相位校正；确定FFT点数N；确定波数v(cm-1)范围v0～v1，如果已知波长λ(μm)则根据公式(7)进转换成波数；对干涉信号直接进行FFT，获得频率v′₁和v′₀。以v0为基准，则有v′₀＝ν₀。根据公式(3)，Δn₁、Δn₀和v'₁均为已知，因此采用牛顿法可以求解出真实的波数v₁，由此完成了波数的修正。对于宽光谱的复色光，可以设定一定的波长间隔Δv，各波长的修正将由程序依次循环完成。最后，将修正后的波数v_n与FFT所得的幅值建立对应关系即可得到修正后光谱曲线。

根据上述步骤，给出以下验证施例：

以双波长混合光干涉数据进行光谱复原，波长分别为0.8μm和1.7μm，对应波数分别为25000cm^-1和5883cm^-1。图2是直接FFT得到的光谱复原曲线，其中1.7μm对应的复原光谱由于晶体双折射的原因已偏离其真实值达423cm^-1，由此可见直接FFT将给偏振干涉的光谱复原带来极大的误差。图3是经过本发明所提修正方法所得的修正光谱曲线，从图可知，0.8μm和1.7μm的光谱均被准确还原。

对于偏振干涉而言,单波长干涉曲线的相位变化与扫描量是线性的，这一点与经典迈克尔逊干涉是一致的，因此无法采用非均匀快速傅里叶变换算法；其次，不同波长余弦曲线的调制频率之比则取决于波数与双折射率差的乘积，因此不能直接采用快速傅里叶变换算法，否则将导致严重的光谱失真。综上所述，传统的快速傅里叶变换和非均匀快速傅里叶变换均无法准确应用于偏振干涉的光谱复原。本发明提出一种偏振干涉光谱复原的修正方法，在快速傅里叶变换的基础上对所得波数按照晶体材料的色散特性进行逐一补偿和修正，最终获得准确的光谱复原。采用快速傅里叶变换算法具有算法成熟、快速和准 确的优点，结合波数修正只需确定相位补偿器的材料属性即可采用软件算法的方式进快速、有效地将直接快速傅里叶变换所得波数逐一补偿。