基于深度学习与复数特征的模拟电路故障诊断方法与流程
本发明属于模拟电路故障诊断技术领域,更为具体地讲,涉及一种基于深度学习与复数特征的模拟电路故障诊断方法。
背景技术:
随着集成电路的快速发展,为了提高产品性能、降低芯片面积和费用,需将数字和模拟元件集成在同一块芯片上。据资料报道,虽然模拟部分仅占芯片面积的5%,但其故障诊断成本却占总诊断成本的95%,模拟电路故障诊断一直是集成电路工业中的一个“瓶颈”问题。
现阶段已经有一些发展的比较完善的模拟电路故障诊断理论应用到实际中了,例如:测前模拟诊断法中的故障字典法测后模拟诊断法中的元件参数辨识法和故障验证法。但这些方法仅限应用于线性系统的工程实际,并且未达到预期的诊断效果,不能解决非线性系统的故障诊断、不能有效诊断多故障和软故障,对具有容差的电路的诊断效果不佳,导致故障误报以及诊断方法的灵敏度降低甚至失灵。
90年代,以神经网络为代表的智能算法为模拟电路故障诊断提供了一条有效途径。但是传统神经网络存在以下几点缺陷:
(1)由于该算法本质上为梯度下降法,而他所要优化的目标函数又非常复杂,因此,必然会出现“锯齿形现象”,这使得神经网络算法低效。
(2)当要解决的问题为求解复杂非线性函数的全局极值时,算法结果很有可能陷入局部极值,致使训练失败。
(3)当算法为多层神经网络时,每次训练会产生误差扩散,这也会导致算法性能变差。
近年来,深度学习成为了机器学习研究中的一个新的领域,随着深度学习逐渐收到各界的广泛关注,其在各个尖端领域的作用也越来越大,深度学习已经在诸多领域取得客观的成就。
模拟电路测点收集的信息是多样化的,比如电压、电流、频率或者相位。那选择什么样的信息,以及怎样处理得到的信息,可以最大化信息有效率,是模拟电路故障诊断需要研究的问题。
技术实现要素:
本发明的目的在于克服现有技术的不足,提供一种基于深度学习与复数特征的模拟电路故障诊断方法,采用自编码网络并结合信号的复数特征,提高模拟电路故障诊断的准确率。
为实现上述发明目的,本发明基于深度学习与复数特征的模拟电路故障诊断方法包括以下步骤:
S1:记模拟电路中故障状态数量为N,测点数量为M,选择K个测试频点,采用仿真软件仿真获取样本数据:设置模拟电路的激励源为交流,首先对模拟电路无故障状态进行仿真,依次设置不同的测试频点,在每个测点处分别测得无故障信号的幅值A0mk和相位θ0mk,m的取值范围为m=1,2,…,M,k的取值范围为k=1,2,…,K;然后对故障状态进行仿真,对于每个故障状态sn,n的取值范围为n=1,2,…,N,设置其对应的故障元件值为故障值,其他故障元件在容差范围内任意选择值,依次设置不同的测试频点,在每个测点处分别测得故障信号的幅值Anmk和相位θnmk;计算无故障状态下每个测点处无故障信号的实数值a0mk=A0mkcosθ0mk和虚数值b0mk=A0mksinθ0mk,构建无故障样本向量V0=(a011,b011,a021,b021,…,a012,b012,a022,b022,…,a0MK,b0MK),并分别计算故障状态sn下每个测点处故障信号的实数值anmk=Anmkcosθnmk和虚数值bnmk=Anmksinθnmk,构建故障样本向量Vn=(an11,bn11,an21,bn21,…,an12,bn12,an22,bn22,…,anMK,bnMK);将每个样本向量中的每个元素归一化至[0,1]范围内,按照故障状态对无故障样本向量和故障样本向量进行标签标记;
S2:采用自编码网络和分类器构成分类网络,然后采用步骤S1得到的无故障样本向量、故障样本向量和对应标签对分类网络进行训练,得到训练好的分类网络;
S3:在模拟电路进行故障诊断时,设置激励源与仿真时相同,依次设置不同的测试频点,在各个测点处测得当前的幅值和相位计算每个测点处信号的实数值和虚数值构建测试样本向量将测试样本向量中的每个元素归一化至[0,1]范围内,然后将其输入步骤S2训练好的分类网络,得到的分类结果即为故障诊断结果。
本发明基于深度学习与复数特征的模拟电路故障诊断方法,采用仿真软件对无故障状态和各个故障状态进行仿真,依次设置不同的测试频点,在每个测点处分别测得无故障信号的幅值和相位,计算得到信号的实数值和虚数值,将实数值和虚数值构建样本向量,并根据故障状态进行标签标记;采用自编码网络和分类器构成分类网络,采用样本向量和对应标签进行训练,然后在模拟电路需要进行故障诊断时,依次设置不同的测试频点,在各个测点处测得当前的幅值和相位,按照同样式构建样本向量,然后输入训练好的分类网络,得到的分类结果即为故障诊断结果。
本发明采用信号的复数特征来构建样本向量,可以更加丰富样本信息,通过自编码网络特征学习提取出更为准确特征,从而提高故障诊断结果的准确度。
附图说明
图1是自编码网络模型的结构图;
图2是本发明基于深度学习与复数特征的模拟电路故障诊断方法的具体实施方式流程图;
图3是本实施例中的sallen-key滤波器电路图;
图4是图3所示滤波器的频响曲线。
具体实施方式
下面结合附图对本发明的具体实施方式进行描述,以便本领域的技术人员更好地理解本发明。需要特别提醒注意的是,在以下的描述中,当已知功能和设计的详细描述也许会淡化本发明的主要内容时,这些描述在这里将被忽略。
实施例
为了更好地说明本发明的技术方案,首先对本发明所基于的深度学习模型进行简要说明。
图1是自编码网络模型的结构图。如图1所示,自编码神经网络尝试学习一个hW,b(x)≈x的函数。换句话说,它尝试逼近一个恒等函数,从而使得输出接近于输入x。当规定隐藏层L2神经元数量小于输入层L1神经元数量时,这就意味着迫使自编码神经网络去学习输入数据的压缩表示。如果输入数据中隐含着一些特定的结构,比如某些输入特征是彼此相关的,那么这一算法就可以发现输入数据中的这些相关性。如果隐藏层神经元数量大于输入层神经元数量,只要在隐含层加上一些稀疏限制,也是可以学到输入数据隐含的特征结构。
自编码神经网络相对于传统神经网络来说,其优势在于两方面,一是需要更少的有标签样本,二是可以设置更多层隐含层,即深度网络。无监督学习可以增大数据集,并且减少人工打标签的工作量。更重要的是可以自主学习出数据中隐含的特征结构,增强数据表达能力。而深度网络最主要的优势在于,它能以更加紧凑简洁的方式来表达比浅层网络大得多的函数集合。正式点说,我们可以找到一些函数,这些函数可以用k层网络简洁地表达出来(这里的简洁是指隐层单元的数目只需与输入单元数目呈多项式关系)。但是对于一个只有k-1层的网络而言,除非它使用与输入单元数目呈指数关系的隐层单元数目,否则不能简洁表达这些函数。
模拟电路故障诊断可以归类为一个模式识别和分类问题。智能算法通过学习各个测点收集的信息,略过了解电路故障模型以及电路特性,就能得出分类结果。在电路特性或者故障模型很复杂的时候,智能算法可以表现出相对于常规经典算法强大的灵活性和自适应性。而自编码神经网络等深度学习方法不仅克服了以神经网络为代表的传统智能算法的缺点,还可以更进一步提高了分类性能,因此本发明基于自编码网络来执行模拟电路故障诊断,可以有效利用自编码网络的优点,提高模拟电路故障诊断的准确率。
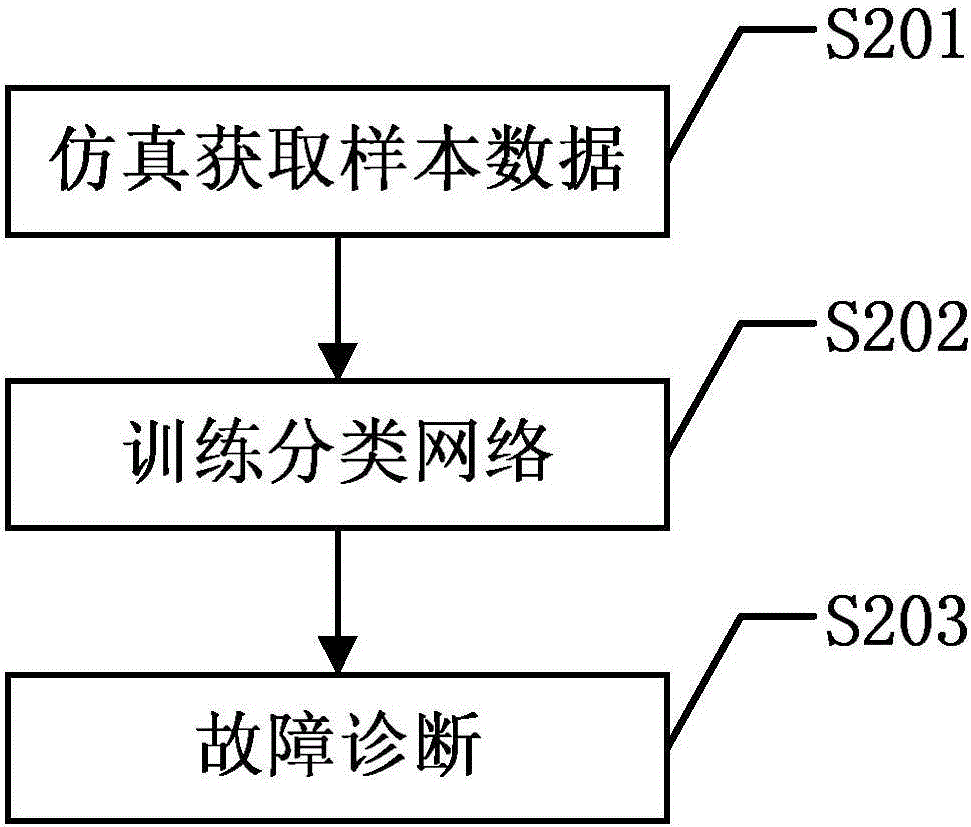
图2是本发明基于深度学习与复数特征的模拟电路故障诊断方法的具体实施方式流程图。如图2所示,本发明基于深度学习与复数特征的模拟电路故障诊断方法的具体步骤包括:
S201:仿真获取样本数据:
记模拟电路中故障状态数量为N,测点数量为M,选择K个测试频点,采用仿真软件仿真获取样本数据:设置模拟电路的激励源为交流,首先对模拟电路无故障状态进行仿真,依次设置不同的测试频点,在每个测点处分别测得无故障信号的幅值A0mk和相位θ0mk,m的取值范围为m=1,2,…,M,k的取值范围为k=1,2,…,K;然后对故障状态进行仿真,对于每个故障状态sn,设置其对应的故障元件值为故障值,其他故障元件在容差范围内任意选择值,依次设置不同的测试频点,在每个测点处分别测得故障信号的幅值Anmk和相位θnmk。在模拟电路中,通常一个故障元件会存在两种故障状态,元件值过大或元件值过小,一般为了更细致精确地诊断故障,需要分别对两种故障状态进行仿真,因此本发明按照故障状态来进行仿真而非故障元件,在实际中可以根据需要来设置需要诊断的故障状态。
对于模拟电路来说,在激励源是交流情况下,每个测点处的信号可以以正弦波形式表示为:
Snmk(t)=Anmksin(ω0t+θnmk)
其中,ω0表示角频率。
转化为复数形式为:
Snmk=Anmkcosθnmk+j*Anmksinθnmk
那么就可以将信号表示为:
Snmk=anmk+j*bnmk
anmk=Anmkcosθnmk
bnmk=Anmksinθnmk
本发明中采用实数值anmk和虚数值bnmk作为样本数据,可以保留幅值和相位两种信息,这样做有两方面好处:
1)加入了相位变化,扩充了样本信息,改善了以前类似技术中只利用了测点的电压峰值或有效值以致于信息过于单一的情况;
2)避免直接使用幅值和相位值构成样本会造成样本中不同维度数据形式不统一,而复数形式中的实部和虚部形式统一,在后面的样本处理中易于归一化。
因此在本发明中,计算无故障状态下每个测点处无故障信号的实数值a0mk=A0mkcosθ0mk和虚数值b0mk=A0mksinθ0mk,构建无故障样本向量V0=(a011,b011,a021,b021,…,a012,b012,a022,b022,…,a0MK,b0MK),并分别计算故障状态sn下每个测点处故障信号的实数值anmk=Anmkcosθnmk和虚数值bnmk=Anmksinθnmk,构建故障样本向量Vn=(an11,bn11,an21,bn21,…,an12,bn12,an22,bn22,…,anMK,bnMK);将每个样本向量中的每个元素归一化至[0,1]范围内,按照故障状态对无故障样本向量和故障样本向量进行标签标记。归一化的原因是在于本发明使用了自编码网络,而自编码网络在训练中需要令输出等于输入,而神经元的输出只在0~1之间,因此需要将样本向量中的每个元素归一化至[0,1]范围内,归一化的方法有很多,本实施例中采用缩放的方式,即归一化公式为:xnew=(xmax-xmin)/xold,其中xnew表示归一化后的数据,xold表示归一化前的数据,xmax、xmin分别表示样本向量所有元素的最大值和最小值。
S202:训练分类网络:
采用自编码网络和分类器构成分类网络,然后采用步骤S201得到的无故障样本向量、故障样本向量和对应标签对分类网络进行训练,得到训练好的分类网络。自编码网络层数可以根据实际需要确定,其输入层节点数量是根据样本向量的元素数量确定的,目前业内具有多种成熟分类器,也是可以根据实际需要来选择的。基于自编码网络的分类网络的训练可以分为三步:首先利用不带标签的数据,进行无监督训练学习到数据特征,然后将学习到的特征作为下一层自编码网络的输入,直到自编码网络学习完毕,然后采用带标签的数据,将自编码网络最后一层特征输入分类器,进行有监督学习微调,从而完成分类网络的训练。基于自编码网络的分类网络是目前一种常用的神经网络,其具体训练过程在此不再赘述。
S203:故障诊断:
在模拟电路进行故障诊断时,设置激励源与仿真时相同,依次设置不同的测试频点,在各个测点处测得当前的幅值和相位计算每个测点处信号的实数值和虚数值构建测试样本向量将测试样本向量中的每个元素归一化至[0,1]范围内,然后将其输入步骤S202训练好的分类网络,得到的分类结果即为故障诊断结果。
为了说明本发明的技术效果,采用一个具体实施例进行仿真验证。图3是本实施例中的sallen-key滤波器电路图。如图3所示,本实施例中该电路图有5个电阻,2个电容,本实施例中只考虑单元件故障,而每个元件有两种故障状态:元件值过大和过小,因此整个电路一共有7*2种故障状态,当然还有一个无故障状态,即15种标签。并且从图3可知,本电路一共有5个测点,这5个测点可以做到全面。为了避免数据冗余,通常会对测点进行选择。根据对本实施例中电路分析得知,测点1记录的是激励源信息,测点3、4记录的信息一样,所以只需测点2、3、5即可记录电路中所有信息。图4是图3所示滤波器的频响曲线。如图4所示,本实施例中sallen-key滤波器的带通频率范围为20kHz~50kHz,为了让训练样本信息更充分,选取多个激励频率测试电路,本实施例中均匀选取中心频率附近的几个频点作为测试频点:10k,15k,25k,35k,70k(Hz)。
对于每个元件,在容差范围内设置其元件值,然后在每个频点下,分别获取各个频点下对应的测点的幅值和相位值,计算得到对应样本数据的实数值和虚数值。由于本实施例中选择了3个测点、5个频点,因此每个样本数据包括15个实数值和15个虚数值,组成一个包含30个元素的样本向量。
对于每一种故障状态,采用Pspice仿真软件通过设置不同元件故障值和蒙特卡洛仿真来增加样本容量。例如,每个元件设置5个同一故障状态下的不同的值,并为每个值设置100次蒙特卡洛仿真。因此本实施例中总样本容量为15*5*100=7500。在这7500条样本中,6500条样本被用来训练,剩下的1000条样本用来测试。表1是图3所示滤波器中各个故障元件的容值范围。
表1
表2是本实施例中样本示例。
表2
对每个样本向量进行归一化处理,将各个元素值限制在[0,1]范围内,以适应自编码网络的需要。
本实施例中采用两层自编码网络,输入层节点数量为15,因此设置其节点数[30,15,30],分类器采用softmax分类器。先采用6500条样本及其对应故障元件标签对由两层自编码网络和分类器构成的分类网络进行训练。然后采用训练好的分类网络对1000条测试样本进行测试。为了说明本发明的技术效果,采用SVM分类器进行分类准确率对比。对分类进行统计得到,采用SVM分类器的分类准确率为93.7%,采用本发明样本数据和分类网络的分类准确率可以达到99.9%,可见,采用本发明可以有效提高模拟电路故障的诊断准确度。
尽管上面对本发明说明性的具体实施方式进行了描述,以便于本技术领域的技术人员理解本发明,但应该清楚,本发明不限于具体实施方式的范围,对本技术领域的普通技术人员来讲,只要各种变化在所附的权利要求限定和确定的本发明的精神和范围内,这些变化是显而易见的,一切利用本发明构思的发明创造均在保护之列。
- 还没有人留言评论。精彩留言会获得点赞!