一种基于存在测量误差的阵列流形先验知识的稳健STAP方法与流程

本发明属于雷达信号处理领域，更具体地，涉及一种基于存在测量误差的阵列流形先验知识的稳健STAP方法。

背景技术：

传统的空时自适应处理(Space-Time Adaptive Processing,STAP)中，诸如主分量法(Principle Components,PC)、局部联合处理(joint domain localized,JDL)算法、根据互谱尺度选择特征子空间方法(Cross-Spectral Metric,CSM)、多级维纳滤波器(Multistage Winer Filter，MWF)算法、联合迭代最优降秩自适应滤波器(JIOAF)法等一系列的降维或降秩算法，将所需的训练样本数目降低为2倍降维后的维度或2倍降秩后的杂波秩。基于多通道矢量自回归(Auto-Regressive,AR)模型的参数自适应匹配滤波(Parametric Adaptive Matched Filter,PAMF)将所需训练样本数从系统空时自由度的2倍降为AR模型阶数的2倍。然而，这些方法相对于非均匀杂波环境来讲，其训练样本数还是很多的。

最近提出的基于阵列流形知识STAP技术，利用诸如载机高度、速度、工作频率、脉冲重复频率(Pulse Repetition Frequency,PRF)、阵列天线指向等先验知识，估计真实环境下的杂波协方差矩阵，进而设计相应的空时滤波器实现杂波抑制和动目标检测。与传统的STAP算法相比，该类算法在杂波非均匀的环境下很大程度上地降低了所需训练样本的个数，并且能更好的适应复杂多变的环境而实现运动目标的检测，展现出优越的性能。然而，该类算法需要较高的计算复杂度，而且其性能依赖于先验知识的准确性，将不利于算法在实际系统的应用。

技术实现要素：

针对现有技术的缺陷，本发明的目的在于提供一种基于存在测量误差的阵列流形先验知识的稳健STAP方法，旨在解决现有技术中由于获得的阵列流形知识存在测量误差，将会对STAP性能带来较大的影响的问题。

本发明提供了一种基于存在测量误差的阵列流形先验知识的稳健STAP方法，包括下述步骤：

S1：根据给定误差范围下获得杂波空时导向矢量集；

S2：利用多个训练样本，在所述杂波空时导向矢量集中寻找重要的空时导向矢量，并计算所述重要的空时导向矢量的特征值和特征向量；

S3：根据所述重要的空时导向矢量的所述特征值和所述特征向量获得杂波协方差矩阵，并根据所述杂波协方差矩阵获得自适应滤波器权矢量。

更进一步地，在步骤S1具体为：

S11：获得单一杂波块的多普勒频率误差最大范围|Δfi,k|＝Δfmax,i,k；其中，i为距离模糊个数索引，i＝1,...,Na，Na为模糊距离环数，k为离散的杂波块个数索引，k＝1,....,Nc，Nc为离散的杂波散射体个数；

S12：根据单一杂波块的多普勒频率误差范围获得杂波块多普勒频率fi,k∈[f′i,k-Δfmax,i,k,f′i,k+Δfmax,i,k]，并根据杂波块多普勒频率构建多普勒频率子空间，将杂波的多普勒频率子空间均匀地划分为Nf等份

其中，f′i,k为依据先验知识计算获得的单一杂波散射体的多普勒频率，Δfmax,i,k为单一杂波散射体多普勒频率的误差最大范围，g为离散的多普勒频率子空间个数索引，Nf为离散的多普勒频率子空间个数，g＝1,...,Nf，fi,k,g为离散的多普勒频率；

S13：根据单一杂波块的方位角φi,k、俯仰角θi,k及多普勒频率fi,k,g获得杂波空时导向矢量

其中，vt(fi,k,g)为时域导向矢量，vs(φi,k,θi,k)为空域导向矢量；

S14：将所有杂波空时导向矢量v(φi,k,θi,k,fi,k,g)构成一个集合，形成杂波空时导向矢量集合Φ。

更进一步地，在步骤S2具体为：

(2.1)初始化：样本集合B0＝[x1,...,xL]，初始空时导向矢量γ0＝φ，终止条件：pmax,ε。

(2.2)获得第1个重要空时导向矢量为

γ1＝{(i1,k1,g1)}，及其特征向量为计算其特征值为和残差向量为bl；1＝bl；0-λl；1uc；1,l＝1,...,L,p＝2；

(2.3)当满足条件且p-1≤pmax时，进行以下迭代过程：

(a)γp＝γp-1∪{(ip,kp,gp)}；

(b)

(c)

(d)bl；p＝bl；p-1-λl；puc；p,l＝1,...,L；

(e)p＝p+1；

(2.4)迭代终止时，获得第p个重要空时导向矢量γ＝γp,相应的特征向量Uc＝[uc；1,...,uc；p]和特征值其中，L为感兴趣距离单元及邻近距离单元得到的多个训练样本数量；||·||∞为l∞范数；pmax为最大迭代次数；ε为正常数，表示迭代残差终止条件。

更进一步地，在步骤S3中，估计得到的真实杂波协方差矩阵为或者其中，p为寻找最重要空时导向矢量时的迭代次数；uc；q为第q个特征向量，p为迭代次数，为第q个特征向量(第q个平均特征值)。

更进一步地，所述自适应滤波器的权矢量其中，为接收热噪声功率估计值，且或diag(·)为对角矩阵。

在本发明中，因阵列流形知识的获取中不可避免的存在误差，将直接导致基于阵列流形知识的STAP的处理性能受限。由于现有技术在考虑阵列流形知识的准确性方面表现欠缺，与现有的基于阵列流形知识的STAP方法相比，本发明降低了对先验知识准确性的要求，对一定误差的先验知识具有稳健的特性，同时在设计滤波器过程中避开杂波协方差矩阵求逆的过程，从而达到了降低系统计算复杂度的目的。

附图说明

图1是本发明实施例提供的一种基于存在测量误差的阵列流形先验知识的稳健STAP方法的实现流程图；

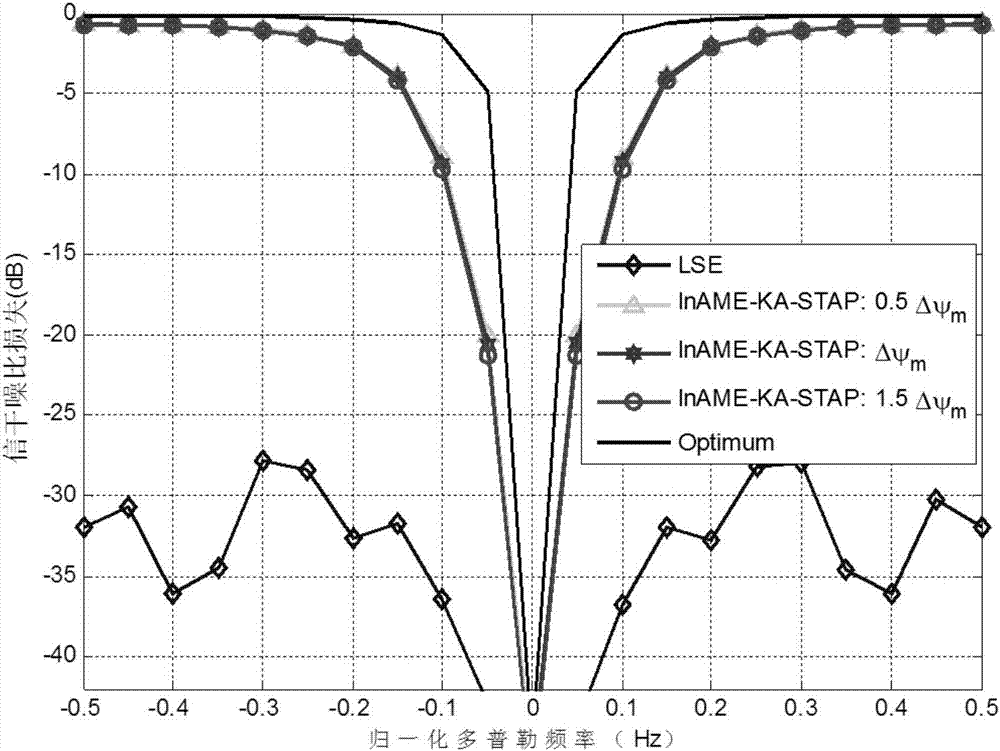
图2是不同的误差下，经典雷达I系统的SINR性能与目标多普勒频率的关系曲线示意图。Δψm为偏航角误差，Δvpm为载机速度误差，其中：(a)为误差Δψm＝0.5°和Δvpm＝1m/s，(b)为误差Δψm＝1°和Δvpm＝1m/s，(c)为误差Δψm＝2.5°和Δvpm＝1m/s，(d)为误差Δψm＝0.5°和Δvpm＝2m/s，(e)为误差Δψm＝0.5°和Δvpm＝3m/s，(f)为误差Δψm＝0.5°和Δvpm＝4m/s；

图3是不同的误差下，经典雷达II系统的SINR性能与目标多普勒频率的关系曲线示意图。Δψm为偏航角误差，Δvpm为载机速度误差，其中，(a)为误差Δψm＝0.5°和Δvpm＝1m/s，(b)为误差Δψm＝1°和Δvpm＝1m/s，(c)为误差Δψm＝2.5°和Δvpm＝1m/s，(d)为误差Δψm＝0.5°和Δvpm＝2m/s，(e)为误差Δψm＝0.5°和Δvpm＝3m/s，(f)为误差Δψm＝0.5°和Δvpm＝4m/s；

图4是雷达I系统分别在正侧视和前视方向，对于不同误差下SINR性能与检测距离关系曲线示意图；其中(a)为正侧视方向，(b)为前视方向；

图5是雷达II系统分别在正侧视和前视方向，对于不同误差下SINR性能与检测距离关系曲线示意图；其中(a)为正侧视方向，(b)为前视方向；

图6是本发明下经典雷达I、II系统的相关系统参数图表；

图7是不同方法下SINR性能曲线示意图；其中(a)为SINR损失(SINRLoss)与训练样本数目关系曲线，(b)为SINR损失(SINRLoss)与目标多普勒频率关系曲线；

图8是不同方法下检测概率Pd与SINR关系曲线示意图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。

本发明涉及雷达信号处理领域，特别是运动目标检测与杂波抑制方向。提出了一种基于存在测量误差的阵列流形先验知识的稳健STAP方法，针对诸如载机速度、偏航角等存在一定误差范围的先验知识，形成真实环境下的杂波空时导向矢量集，进而实现少量训练样本估计真实环境下的杂波协方差矩阵，最后设计具有计算复杂度低的稳健STAP滤波器，从而实现杂波抑制与目标检测的目的。

本发明为了降低存在测量误差的先验知识对STAP方法性能的影响，以及估计协方差矩阵时计算复杂度高的问题，提出了一种基于存在测量误差的阵列流形先验知识的稳健STAP方法。

理想条件下，含有杂波与噪声的空时快拍模型可表示为：x＝Vσ+n；其中，为杂波的导向词典，v(φi,k,θi,k,fi,k)为第ik个杂波块的导向矢量，fi,k＝2vpcosθi,ksin(φi,k+ψ)/λc(vp,λc,ψ分别为载机速度、波长和偏航角)为多普勒频率，φi,k,θi,k,分别为方位角、俯仰角。σ为所有杂波块的复幅度，n为均值零，方差为的高斯白噪声。

实际中，我们获得的诸如载机速度、偏航角等先验知识是存在误差的，这将导致实际中与假定的杂波空时导向矢量存在偏差。该发明正是基于不准确的阵列流形先验知识条件下，设计一种基于存在测量误差的阵列流形先验知识的稳健STAP方法。本发明的核心思想是：利用杂波模型中不准确的阵列流形先验知识，估计真实环境下的杂波协方差矩阵，设计稳健的空时滤波器而实现杂波抑制与目标检测。

本发明实施例提供的一种基于存在测量误差的阵列流形先验知识的稳健STAP方法该具体包括下述步骤：

(1)利用给定误差范围的先验知识形成真实环境下的杂波空时导向矢量集；

假设实际系统中测量得到的载机速度和偏航角分别为v′p、ψ′，且有

v′p∈[vp-Δvpm,vp+Δvpm]、ψ′∈[ψ-Δψm,ψ+Δψm]

内分别服从均匀分布，载机速度和偏航角的误差分别为Δvp＝v′p-vp、Δψ＝ψ′-ψ，并且有|Δvp|≤Δvpm和|Δψ|≤Δψm。因而，可计算单一杂波块的多普勒频率误差范围为：

因此，实际中的杂波块多普勒频率fi,k∈[f′i,k-Δfmax,i,k,f′i,k+Δfmax,i,k]可以构成一个多普勒频率子空间。将杂波的多普勒频率子空间均匀地划分为Nf等份因而根据单一杂波块的方位角φi,k、俯仰角θi,k及真实的多普勒频率fi,k,g，可以得到真实的杂波空时导向矢量其中，表示Kronocker积，vt(fi,k,g)、vs(φi,k,θi,k)分别为第ik个杂波块的时域、空域导向矢量。将所有的空时导向词典v(φi,k,θi,k,fi,k,g)i＝1,...,Na，k＝1,....,Nc，g＝1,...,Nf形成杂波空时导向矢量集合Φ。

(2)从得到的杂波空时导向矢量集合中，找出最重要的空时导向矢量并计算相应的特征值和特征向量；

该步骤是本发明中核心的思想，根据某一感兴趣距离单元的训练样本x，并提出了一种类似于正交匹配追踪的方法，从得到的杂波空时导向矢量集合Φ中选出重要的空时导向矢量，并计算相应的特征向量Uc＝[uc；1,uc；2,...]和特征值λ＝[λ1,λ2,...]^T。

具体的方法流程如下所示：

(2.1)初始化：设定初始空时导向矢量为γ0＝φ，残差向量b0＝x

(2.2)迭代次数p＝1时：从集合Φ中找到首个最重要的矢量为γ＝{i1,k1,g1}；

计算相应的特征向量和特征值经过第一次迭代后的残差向量b1＝b0-z1uc；1。

(2.3)迭代次数p≥2时：假设已找到第p-1个重要的空时导向矢量为γp-1，且残差向量为bp-1，则第p个重要空时导向矢量为γp＝γp-1∪{(ip,kp,gp)}，计算相应的特征向量

(2.4)终止条件：当迭代次数达到设定的迭代极值(即p≥pmax)或满足条件||Φ^Hbp||∞≤ε(其中||·||∞为l∞范数，ε为正常数)时，需要对上述迭代过程进行终止。因而，最终得到的最重要杂波空时导向矢量为γ＝γp，相应的特征向量为Uc＝[uc；1,uc；2,...uc；p]，特征值为λ＝[λ1,λ2,...λp]^T。

为了提高选取的空时导向矢量的准确性，本发明可以利用感兴趣距离单元及邻近距离单元得到多个训练样本，挑选出最重要的空时导向矢量γ，并计算其特征向量与特征值。假定由L个训练样本构成的样本矩阵为X＝[x1,...,xL]，残差矩阵为B＝[b1,...,bL]，特征值矩阵Λ＝[λ1,...,λL]

利用多个样本找出γ，计算特征向量Uc和特征值方法过程为：

(2.2.1)初始化：B0＝[x1,...,xL],γ0＝φ，终止条件：pmax,ε。

(2.2.2)首个矢量γ：γ1＝{(i1,k1,g1)}，bl；1＝bl；0-λl；1uc；1,l＝1,...,L,p＝2。

(2.2.3)满足条件且p-1≤pmax时，进行以下迭代过程

(a)γp＝γp-1∪{(ip,kp,gp)},

(b)

(c)

(d)bl；p＝bl；p-1-λl；puc；p,l＝1,...,L,

(e)p＝p+1。

(2.2.4)γ＝γp,Uc＝[uc；1,...,uc；p],且其中

(3)估计杂波协方差矩阵，设计稳健的空时滤波器。

利用得到的最重要导向矢量的特征向量Uc与特征值λ(或)来估计真实的杂波协方差矩阵，从而设计稳健的空时滤波器实现杂波抑制与目标检测。

估计得到的杂波协方差矩阵为或者因而空时自适应处理自适应滤波器的权矢量为其中为接收热噪声功率估计值，且

或

在上述的滤波器权矢量求解过程中，避免了杂波的协方差矩阵求逆这一过程，与传统的STAP滤波器权矢量求解相比，具有降低系统计算复杂度、节约实际成本等优势。

为了更进一步的说明本发明实施例提供的一种基于存在测量误差的阵列流形先验知识的稳健STAP方法，现将本发明与现有的技术进行比较来说明本发明的有益效果；具体分析如下：

由于本发明下需要知道先验知识机载速度vp与偏航角ψ的误差范围，该部分将从不同机载速度和偏航角的误差下，分析系统的信干噪比(SINR)与目标的多普勒频率的关系并与现有方法进行比较。

从图2、图3可以得知，本发明在不同测量误差的条件下，相比LSE方法(直接利用测量的机载速度和偏航角形成的空时导向矢量设计的STAP滤波器)具有更好的性能。这是由于测量误差的存在，LSE方法中形成的空时导向矢量并不能表示真实的导向矢量，使得估计得到的杂波协方差矩阵不够准确，从而降低了杂波抑制的性能。然而，本发明下的方法能对各类误差都保持较好的性能，展现出很好的稳健性，这是由于所提方法将测量误差考虑到假设的空时导向矢量中，在一定程度上包含了或者近似包含了真实的杂波子空间。

由图4、图5可得知，该发明下的方法相对LSE方法而言，在先验知识存在测量误差的条件下仍具有更好的性能，展现出较好的稳健性。同时，距离模糊问题的存在对两种方法的SINR性能影响较小。尽管由于距离模糊导致在高脉冲重复频率雷达下本发明的SINR性能下降1-2dB，但在高计算复杂度的前提下是可接受的。图6示出了本发明下经典雷达I、II系统的相关系统参数。

为了充分体现本发明具有的优势，本部分将通过SINR性能和PD性能指标与其它方法进行比较。主要比较的方法有：4×3JDL方法、PAMF方法、CSMIECC方法、Stoica方案、KAPE方法、基于阵列流形知识的PAMF方法等。

从图7(a)可以得出，本发明能利用单个训练样本获得低于最优空时滤波器性能-2dB的效果；基于阵列流形知识下的方法相比传统的STAP方法而言，具有更好的准确性和收敛性，这是由于前者利用了先验知识来计算杂波的协方差矩阵。从图7(b)中SINR性能与目标多普勒关系曲线图中可以得出，基于先验知识下的方法能在少量样本甚至单个样本的展现出更好的性能，本发明相比其他方法具有更好的优势。由图8中可知，相比传统的STAP方法，本发明及基于阵列流形先验知识的方法具有更好的目标检测性能。

总而言之，本发明中提出的方法在假设的空时导向矢量中考虑了阵列流形知识的测量误差，对构成的杂波子空间进行过采样形成真实的杂波导向矢量，并选出最重要的空时导向矢量，相比LSE方法而言能够更加精确地获得杂波子空间。同时，本发明相比传统的SATP方法能在单个训练下获得更好的杂波抑制效果，并比现有的基于阵列流形知识(存在误差)STAP方法拥有更好的SINR性能和目标检测性能。

本领域的技术人员容易理解，以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。