一种基于LM算法分解激光雷达波形确定海水深度的方法与流程

本发明涉及一种对激光雷达回波波形数据处理的方法，是一种通过LM算法实现激光雷达波形数据分解的方法，属于机载激光雷达技术领域。

背景技术：

水深测量是海洋测绘的重要内容。传统的船载多波束回声测深方法虽然具有较高的测量精度，但无法进入沿岸浅水区域和海礁密集区域。近年来，机载激光雷达的出现和发展填补了沿海浅水区域水深测量技术的空白，已成为一种快速高效的水深及海底地形探测方法。机载激光雷达探测系统可以广泛用于海洋水文勘测(包括海水深度测量、海底地貌测绘和海水光学参数遥测等)、水雷和鱼群的探测、海洋环境污染监测等众多领域，因而在海洋科学研究中有巨大的作用。

机载激光雷达系统在海洋探测领域有着探测精度高、探测效率高、不受海水温度和盐度影响等优势。机载激光雷达系统的工作原理是机载激光发射器向海面发射激光，通过计算海面回波和海底回波的时间差求解出海水深度。为了提高水深测量精度，需求解出激光的精确回波时间，但是由于海水的组成十分复杂，增加了对回波波形的数据处理难度，无法求出精确的回波时间。因此对波形数据的处理方法就变得尤为重要。

目前波形数据的处理算法主要有三种：一是阈值法，二是形心法，三是波形分解法。阈值法在面对较为复杂的回波时，由于未考虑光斑内不同目标物回波间的相互影响，使得处理结果的准确性上存在一定问题。对于形心法，当待测目标的回波波形出现上升沿或者下降沿变缓、波形发生展宽和畸变时，可能会出现较大的偏差。波形分解法将不同高度处的目标物回波从接收的波形信号中提取出来，采用高斯函数近似刻画单个目标的回波波形。波形分解法可以将由于水深较浅而重叠为一个波峰的海面与海底回波分解以判断海面与海底回波的对应位置。传统方法使用EM(Expectation Maximization)算法进行波形分解，但是EM算法存在收敛速度较慢等问题。

技术实现要素：

本发明使用LM算法进行波形分解。LM(Levenberg-Marquardt)算法是一种利用标准数值优化技术的快速算法，既有高斯-牛顿法的局部收敛性，又有梯度下降法的全局特性。在设定合理初值的情况下，能得到可靠的最优参数。本发明中，当得到激光的回波波形时，有效地将海面回波与海底回波分解为两个波形，利用两个回波的时间差求出海水深度。

为了解决上述技术问题，本发明提出的一种基于LM算法分解激光雷达波形确定海水深度的方法，通过激光雷达接收获得海面回波与海底回波构成的总体回波，并包括以下步骤：

步骤一、波形预处理，包括波形的噪声去除和波形平滑；其中，波形的噪声去除中在进行噪声估计时，将总体回波数据采集点的前2.5％的点和后2.5％的点幅值的平均值作为噪声的均值；选择高斯函数对上述总体回波的波形进行平滑处理；

步骤二、对于海面回波及海底回波波形参数的初始化，包括：

对于海面回波，采用式(1)所示的高斯函数与指数函数的卷积模拟海面回波波形，以增加时间常数τ以模拟后向散射对海面回波波形的影响；

式(1)中的初始参数包括：函数幅值h_G、时间常数τ、海面回波波峰的对应时间t_G及高斯函数的标准差σ_G；自变量为t

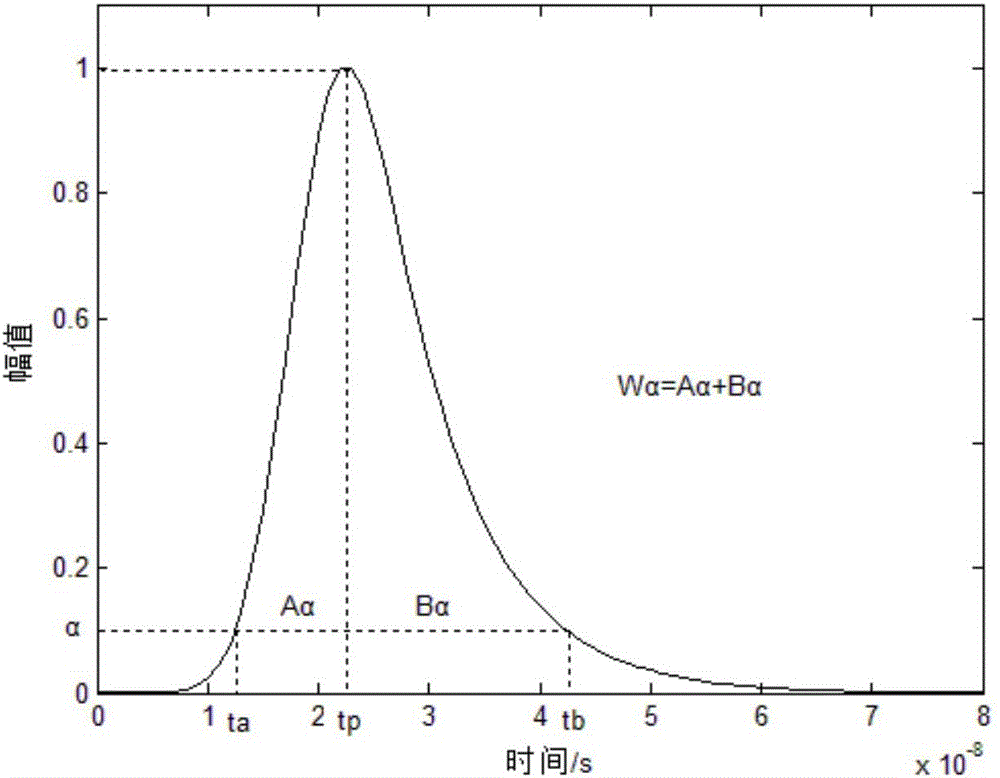
总体回波最大峰值点对应的幅值为A，总体回波最大峰值点对应时间为t_p，求出幅值为A'＝α×A处所对应的时间t_a和时间t_b，t_a＜t_b，幅值系数α＝0.1；

设：

W_α＝t_b-t_a (2)

A_α＝t_p-t_a (3)

B_α＝t_b-t_p (4)

式中：t_b与t_a的时间间隔为W_α、t_p与t_a的时间间隔为A_α、t_b与t_p的时间间隔为B_α及中间参数μ；

则

t_G＝t_p-σ_G[-0.193(B_α/A_α)²+1.162(B_α/A_α)-0.545] (8)

将式(6)、式(7)和式(8)代入式(1)中，求解出函数幅值h_G；

对于海底回波，使用式(9)所示高斯函数代表海底回波信号，

y_G(t)＝A_maxexp[-(t-t_max)²/2σ²] (9)

式(9)中的初始参数包括：高斯函数的最大幅值A_max，海底回波波峰的对应时间t_max，σ标准差；

将总体回波波形减去初始的海面回波波形得到海底回波波形，海底回波波形的最大峰值点的波峰对应的幅值为A_max，海底回波波形对应的时间为t_max，若激光雷达发射脉冲的半宽为ω，则取

步骤三、对步骤二初始化后的参数进行最优化：

利用LM算法通过迭代对初始波形参数进行优化，设x为含有n个参数的向量；e_k(x)＝y(x，t_k)-y(t_k)为每个采样点的残差，t_k为在第k个采样点的时间；目标函数为

E(x)的二次模型为m(x+s)＝E(x)+g(x)^Ts+0.5s^TH(x)s,其中s为步长，g(x)为E(x)的梯度，H(x)为E(x)的Hessian矩阵；

设e(x)的雅克比矩阵为J(x)，e(x)＝[e₁(x)，…,e_k(x)，…，e_m(x)]^T，其中m为采样点的数量；

则E(x)＝e(x)^Te(x)，g(x)＝2J(x)^Te(x)，H(x)＝2J(x)^TJ(x)；

对于LM算法，步长为s(λ)＝-[λI+J(x)^TJ(x)]-¹J(x)^Te(x)，λ为阻尼参数，I为n阶单位矩阵，n为参数个数；

所述LM算法的具体过程如下：

3-1)设置参数组成的向量x₀及置信半径初值δ，求E(x₀)；

3-2)设λ＝0，求s(λ)和||s(λ)||₂；

3-3)若||s(λ)||₂≤1.5δ，则设调整向量s＝s(λ)，δ＝min{δ，s(λ)}，转到步骤3-5)；

3-4)若||s(λ)||₂＞1.5δ，寻找一个当次迭代阻尼参数λ_k，使||s(λ_k)||₂∈[0.75δ，1.5δ]，设s＝s(λ_k)；

3-5)设调整后的参数向量x₊＝x₀+s，求E(x₊)，计算实际变化量ΔE＝E(x₊)-E(x₀)；

3-6)若ΔE≥0，则取δ∈[0.1δ，0.5δ]，并返回步骤3-4)；

3-7)计算m(x₊)，设预计变化量ΔE_pred＝m(x₊)-E(x₀)，实际变化量与预计变化量的比值R＝ΔE/ΔE_pred若R≤0.1，则δ＝0.5δ，若R≥0.75，则δ＝2δ，否则δ不变；

3-8)若|s|/(0.001+|x₀|)≥0.1，则设x₀＝x₊，并返回步骤3-2)，否则最优化的参数x_f＝x₊，E_f＝E(x₊)，停止计算，得到最优化的参数x_f，并将该最优化的参数x_f分别带入式(1)和式(9)，从而获得海面回波波形与海底回波波形；

步骤四、求解海水深度D：通过步骤三得到的海面回波波峰的对应时间t_G和海底回波波峰的对应时间t_max求出海水深度其中c为光速，n_w为海水折射率。

与现有技术相比，本发明的有益效果是：

利用LM算法可以得到最优参数，实现海面回波与海底回波的分解，大大减少算法复杂程度。在海面回波与海底回波十分接近的情况下(如图2)，仍可以分解出海面波形和海底波形。

附图说明

图1是本发明中总体回波波形分解流程图；

图2是本发明中对海面回波进行初始参数的估计；

图3是本发明中对参数进行最优化后获得的波形分解效果图。

具体实施方式

下面结合附图和具体实施例对本发明技术方案作进一步详细描述，所描述的具体实施例仅对本发明进行解释说明，并不用以限制本发明。

本发明提出的一种基于LM算法分解激光雷达波形确定海水深度的方法，其设计思路如图1所示，在得到回波波形后，进行回波波形分解操作，即，首先对波形进行降噪和平滑处理；然后，根据回波波形设定初始波形参数；其次，通过LM算法拟合，在每次迭代调整参数，当迭代计算符合结束条件时，求得最优参数；最后，将回波波形分解为海面波形与海底波形，进而求解出海水深度。具体步骤如下：

步骤一、波形预处理，包括波形的噪声去除和波形平滑；其主要目的是减少波形中的噪声对参数初值设定的干扰。波形的噪声去除中在进行噪声估计时，将总体回波数据采集点的前2.5％的点和后2.5％的点幅值的平均值作为噪声的均值(若有2000个采样点则取前50和后50个采样点求解平均值)；需选择高斯函数作为滤波器，因此，选择高斯函数对上述总体回波的波形进行平滑处理；

步骤二、对于海面回波及海底回波波形参数的初始化，包括：

对于海面回波：

采用式(1)所示的高斯函数与指数函数的卷积模拟海面回波波形，以增加时间常数τ以模拟后向散射对海面回波波形的影响；

式(1)中的初始参数包括：函数幅值h_G、时间常数τ、海面回波波峰的对应时间t_G及高斯函数的标准差σ_G；自变量为t

如图2所示，求出的总体回波最大峰值点对应的幅值为A，总体回波最大峰值点对应时间为t_p，求出幅值为A'＝α×A处所对应的时间t_a和时间t_b，t_a＜t_b，幅值系数α＝0.1；

设：

W_α＝t_b-t_a (2)

A_α＝t_p-t_a (3)

B_α＝t_b-t_p (4)

式中：t_b与t_a的时间间隔为W_α、t_p与t_a的时间间隔为A_α、t_b与t_p的时间间隔为B_α及中间参数μ；

则

t_G＝t_p-σ_G[-0.193(B_α/A_α)²+1.162(B_α/A_α)-0.545] (8)

将式(6)、式(7)和式(8)代入式(1)中，求解出函数幅值h_G。

对于海底回波：

使用式(9)所示高斯函数代表海底回波信号，可以减少算法复杂度。

y_G(t)＝A_maxexp[-(t-t_max)²/2σ²] (9)

式(9)中的初始参数包括：高斯函数的最大幅值A_max，海底回波波峰的对应时间t_max，σ标准差；

将总体回波波形减去初始的海面回波波形得到海底回波波形，海底回波波形的最大峰值点的波峰对应的幅值为A_max，海底回波波形对应的时间为t_max，若激光雷达发射脉冲的半宽为ω，则取

步骤三、对步骤二初始化后的参数进行最优化：

利用LM算法通过迭代对初始波形参数进行优化，设x为含有n个参数的向量；e_k(x)＝y(x，t_k)-y(t_k)为每个采样点的残差，t_k为在第k个采样点的时间；目标函数为

E(x)的二次模型为m(x+s)＝E(x)+g(x)^Ts+0.5s^TH(x)s,其中s为步长，g(x)为E(x)的梯度，H(x)为E(x)的Hessian矩阵；

设e(x)的雅克比矩阵为J(x)，e(x)＝[e₁(x)，…,e_k(x)，…，e_m(x)]^T，其中m为采样点的数量；

则E(x)＝e(x)^Te(x)，g(x)＝2J(x)^Te(x)，H(x)＝2J(x)^TJ(x)；

对于LM算法，步长为s(λ)＝-[λI+J(x)^TJ(x)]-¹J(x)^Te(x)，λ为阻尼参数，I为n阶单位矩阵，n为参数个数；

所述LM算法的具体过程如下：

3-1)设置参数组成的向量x₀及置信半径初值δ，求E(x₀)；

3-2)设λ＝0，求s(λ)和||s(λ)||₂；

3-3)若||s(λ)||₂≤1.5δ，则设调整向量s＝s(λ)，δ＝min{δ，s(λ)}，转到步骤3-5)；

3-4)若||s(λ)||₂＞1.5δ，寻找一个当次迭代阻尼参数λ_k，使||s(λ_k)||₂∈[0.75δ，1.5δ]，设s＝s(λ_k)；

3-5)设调整后的参数向量x₊＝x₀+s，求E(x₊)，计算实际变化量ΔE＝E(x₊)-E(x₀)；

3-6)若ΔE≥0，则取δ∈[0.1δ，0.5δ]，并返回步骤3-4)；

3-7)计算m(x₊)，设预计变化量ΔE_pred＝m(x₊)-E(x₀)，实际变化量与预计变化量的比值R＝ΔE/ΔE_pred若R≤0.1，则δ＝0.5δ，若R≥0.75，则δ＝2δ，否则δ不变；

3-8)若|s|/(0.001+|x₀|)≥0.1，则设x₀＝x₊，并返回步骤3-2)，否则最优化的参数x_f＝x₊，E_f＝E(x₊)，停止计算，得到最优化的参数x_f，并将该最优化的参数x_f分别带入式(1)和式(9)，从而获得海面回波波形与海底回波波形，波形分解的效果如图3所示。

步骤四、求解海水深度D：通过步骤三得到的海面回波波峰的对应时间t_G和海底回波波峰的对应时间t_max求出海水深度其中c为光速，n_w为海水折射率。

尽管上面结合附图对本发明进行了描述，但是本发明并不局限于上述的具体实施方式，上述的具体实施方式仅仅是示意性的，而不是限制性的，本领域的普通技术人员在本发明的启示下，在不脱离本发明宗旨的情况下，还可以做出很多变形，这些均属于本发明的保护之内。