ENPEMF数据的格林函数‑SPWVD时频分析方法与流程

本发明涉及一种ENPEMF数据的格林函数-SPWVD时频分析方法，属于非平稳数据的时频分析处理领域。

背景技术：

地震给人类的生活带来了巨大的灾难，据统计，全球的自然灾害之中，地震造成的死亡人数占全部自然灾害死亡人数的54％，堪称自然灾害之最。如何预测地震一直以来都是一个热门敏感的话题。然而，因地震预测有着地球内部的“不可入性”、大地震的“非频发性”、“地震物理过程的复杂性”三大困难，地震预测成为了公认的世界性难题，对于地震前兆预测对于人类生命安全和社会财产安全的具有很大的意义。

在现有的孕震信息研究过程中，由现有的信号采集装置采集到的地球天然脉冲电磁场(ENPEMF)信号由于其本身存在时频分布不准确的问题，需要经过繁杂的处理才能输出为稳定的二维时频谱，再做进一步分析。

在现有的孕震信息研究过程中，STFT与WVD时频分析方法是常用的用来对采集到的大量地球天然脉冲电磁场信号进行分析的方法。传统的STFT或WVD时频分析方法会用到以下公式对地球天然脉冲电磁场信号进行处理：

传统的STFT或WVD时频分析方法需要设置阀值c以及幂调节系数a和b。其中c为STFT谱的交叉项消除阀值。当STFT谱的值小于该阀值时返回0，如果大于该阀值则返回1。WVD中有交叉项对应STFT谱部分的数值肯定小于该阀值，用数字0与WVD相乘以消除交叉项；其中a和b式为幂调节系数，作用是增强两变换数值较大部分而消弱有交叉项部分。式(a)所示方法灵活性差，输入信号幅值或能量大小直接影响c值的选择，目前没有人能提出一种行之有效的自适应阀值选择方法，并且在实际信号中有用分量幅值、能量大小往往各不相同甚至差别较大，因此采用设置阀值消交叉项容易也将信息项消除；式(b)所示方法有些许改进，但同样幂调节系数的确定没有理论基础，如何根据待分析信号的特征确定幂调节系数有待进一步研究，对使用造成不便，同时存在难于避免的交叉项干扰，往往需要进一步利用滤波等方法对得到的信号进行进一步处理，才能得到便于解读的时频图和谱图。

技术实现要素：

为了解决现有技术的不足，本发明提供了一种ENPEMF数据的格林函数-SPWVD时频分析方法，可以处理地球天然脉冲电磁场信号数据，获取较为明显的震前时频能量谱的分布异常，得出基于地球天然脉冲电磁场分析孕震信息的有效性，该方法的结构新颖，效果良好，满足科学分析研究的需要，对地震前兆研究以及非平稳信号的研究有积极的意义。

本发明为解决其技术问题所采用的技术方案是：提供了一种ENPEMF数据的格林函数-SPWVD时频分析方法，包括以下步骤：

(1)对原始ENPEMF数据进行平滑压缩预处理；

(2)针对步骤(1)中平滑压缩后的ENPEMF数据，采用基于泊松方程的格林函数进行处理，得到格林函数化的ENPEMF数据；

(3)对经步骤(2)处理得到的格林函数化的ENPEMF数据，采用平滑伪WVD算法进行扫频处理；

(4)对经步骤(3)处理得到的数据，进行时频分析汇总，得出原数据的时间-频率联合分布图。

步骤(1)所述平滑压缩预处理采用平方平均算法。

步骤(2)所述针对步骤(1)中平滑压缩后的ENPEMF数据，采用基于泊松方程的格林函数进行处理，得到格林函数化的ENPEMF数据，具体包括将基于泊松方程的格林函数正规化，再将平滑压缩后的ENPEMF数据代入正规化后的格林函数得到格林函数化的ENPEMF数据。

步骤(3)所述对经步骤(2)处理得到的格林函数化的ENPEMF数据，采用平滑伪WVD算法进行扫频处理，具体过程为：设格林函数化的ENPEMF数据用以下叠加信号形式表示：

其中，φ₁(t)和φ₂(t)为相位；则利用以下公式对格林函数化的ENPEMF数据进行时频分析变换：

其中，t和f分别为格林函数化的ENPEMF数据的时域变量和频域变量，是格林函数化的ENPEMF数据在时频和频域的各自成分特点描述；u和τ分别表示格林函数化的ENPEMF数据的时域积分变量和频域积分变量，g(u)和h(τ)为设置的实偶窗函数。

实偶窗函数g(u)、h(τ)均采用高斯窗。

本发明基于其技术方案所具有的有益效果在于：

(1)本发明充分利用了格林函数的叠加思想：格林函数是表示一种特定的场和产生这种场的源之间的数学物理方程，即当一个源被分解成很多点源的叠加时，如果能知道分解后每个点源产生的场，利用叠加原理就可以求出同样边界条件下任意源的场；本发明基于格林函数的叠加思想，将原信号首先经过格林函数分解，能够加强频率的分布效果；再对经格林函数分解后的信号进行SPWVD算法的扫频分解，最后得到原始信号的时间-频率联合分布；

(2)本发明可以较好的降噪和降低WVD扫频时产生的交叉项，并且结构新颖，步骤简单，在针对大量繁杂地球天然脉冲电磁场(ENPEMF)数据分析时能够提高处理效率，具有良好的应用前景；

(3)本发明针对特殊的非平稳ENPEMF数据采用平方平均算法进行平滑压缩处理，与算术平均、几何平均、调和平均等平滑压缩处理方法相比，平方平均算法压缩后的数据包络与原数据包络一致性最高，效果最优；

(4)经大量仿真实验论证，本发明与传统的STFT方法、小波变换(Wavelet)方法相比，能够得到效果最优的时频分布图。

附图说明

图1是本发明的一种ENPEMF数据的格林函数-SPWVD时频分析方法的流程示意图。

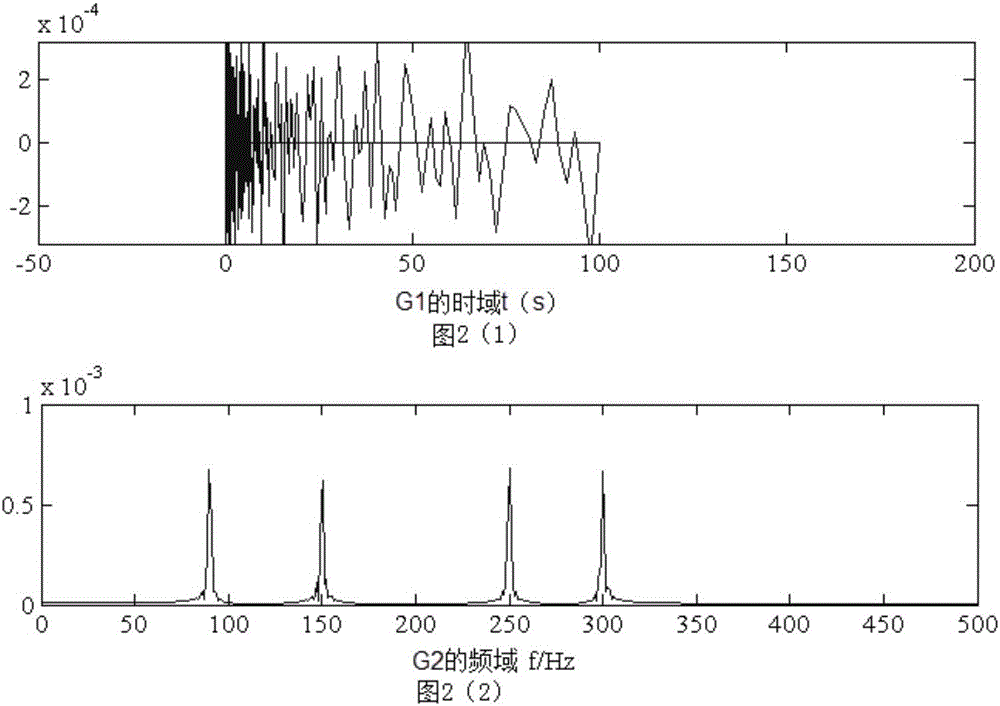
图2是本发明实施例信号G1的FFT频率分布图，其中图2(1)是为时域图，图2(2)为频域图。

图3是本发明实施例信号G1的STFT时频图。

图4是本发明实施例信号G1的Wavelet时频图。

图5是本发明实施例信号G1的WVD时频图。

图6是本发明实施例信号x1的直接SPWVD时频图。

图7是本发明实施例信号G1的SPWVD时频图。

图8是本发明实施例信号G2的FFT频域图。

图9是本发明实施例信号G2的STFT时频图。

图10是本发明实施例信号G2的Wavelet时频图。

图11是本发明实施例信号G2的WVD时频图。

图12是本发明实施例信号x2直接WVD时频图。

图13是本发明实施例信号x2直接SPWVD时频图。

图14是本发明实施例信号G2的SPWVD时频图。

图15是本发明实施例420CN2AH的FFT时频图。

图16是本发明实施例420CN2AH的格林函数化后的SPWVD时频图。

图17是原始ENPEMF数据1的时间-脉冲数示意图。

图18是原始ENPEMF数据1的不同压缩方法处理效果比较示意图。

图19是原始ENPEMF数据2的日期-脉冲数示意图。

图20是原始ENPEMF数据2的不同压缩方法处理效果比较示意图。

具体实施方式

下面结合附图和实施例对本发明作进一步说明。

本发明提供了一种ENPEMF数据的格林函数-SPWVD时频分析方法，参照图1，包括以下步骤：

(1)对原始ENPEMF数据进行平滑压缩预处理；所述平滑压缩预处理采用平方平均算法，效果最优。

如图17至图20所示，给出了两组原始ENPEMF数据用不同的压缩方法处理的效果比较，可以很明显对比出平方平均方法处理得到的数据最接近原始ENPEMF数据的波动韵律，再经过后续步骤进行分析，可以最大程度保证数据有效性。

(2)针对步骤(1)中平滑压缩后的ENPEMF数据(即多频信号s)，采用基于泊松方程的格林函数进行处理，得到格林函数化的ENPEMF数据；

基于泊松方程的格林函数为：

为得到正确结果，将公式1进行正规化得到以下公式：

公式2中，m为引入的一个无穷小的质量参数，r＝|x|，此时再令m→0，得：

公式3即为正规化后的格林函数。将多频信号s作为变量代入公式3，即得到格林函数化的ENPEMF数据；

(3)对经步骤(2)处理得到的格林函数化的ENPEMF数据，采用平滑伪WVD算法进行扫频处理；

通常，一个叠加信号的WVD分布包括以下四项：

前两项为信号自身项(Signalterms)，后两项就是交叉干扰项(Crossterms)，即为需要抑制的由于算法变换产生的噪声分量。

假设格林函数化的ENPEMF数据用以下叠加信号形式表示：

其中，φ₁(t)和φ₂(t)为相位，s(t)确定后φ₁(t)、φ₂(t)以及j即可确定。

将信号(公式5)代入公式4，得：

前两项自身项不是信号瞬时频率支撑区内的任何分量，来自自身项的叠加，表现出交叉项的特点。

以式(公式6)的第一项来分析，将φ₁(t)按照Taylor级欺展开得到：

由公式7可知，由属于同一个信号分量的不同部分之间相互作用产生的内部交叉项(自交叉项)也是干扰噪声源之一，有别于由不同的信号分量之间相互作用造成的外部交叉项。这两项都是需要采用合适的方法来去除或抑制。

在存在多个信号分量的情况下，原始信号的WVD时频图之间产生的交叉项将十分显著。并且，当信号分量越多时，其交叉项分布也就越复杂。为了抑制交叉项，出现一种WVD的改良算法，即平滑伪WVD，简称SPWVD。

在WVD(公式4)的基础上增加两个窗函数，改良为SPWVD，其定义如下：

公式8中，其中，t和f分别为格林函数化的ENPEMF数据的时域变量和频域变量，是格林函数化的ENPEMF数据在时频和频域的各自成分特点描述；u和τ分别表示格林函数化的ENPEMF数据的时域积分变量和频域积分变量，格林函数化的ENPEMF数据确定后u和τ即可确定。

g(u)和h(τ)为设置的实偶窗函数，且h(0)＝g(0)＝1，SPWVD的作用实质是相当于WVD在时域和频域方向同时进行平滑滤波处理。通过调整上述两个窗g(u)、h(τ)的宽度，可以有效的抑制交叉项。需要注意的是，时频图的分辨率与窗的宽度大小成反比。因此，根据实际需求来选取合适的窗将变得尤为重要。g(u)、h(τ)的形状可选择矩形窗、高斯窗、布莱克曼、汉明窗、汉宁窗等，这些形状的窗各有优缺点，针对ENPEMF数据的非周性、非平稳性，由于高斯窗具有最好的时宽-带宽乘积(等于1/2)，效果相对较好，这里的两个窗函数都选择高斯窗。

由上述步骤(2)中得到格林函数化的ENPEMF数据G(x)，然后再对G(x)信号按SPWVD方法(公式8)进行时频分析变换，即完成平滑伪WVD算法进行扫频处理。

(4)对经步骤(3)处理得到的数据，进行时频分析汇总，得出原数据的时间-频率联合分布图。具体根据数据分析的需要，采用matlab中的画图输出函数plot()，可输出二维时频图，也可输出三维时频图；可绘制单天的数据时频分析，也可绘制多天的数据时频分析进行对比研究；可以单幅图像输出，也可多幅图像对比输出等等。即根据分析要求和目的采用有针对性的时频分析汇总。

对本发明的效果进行仿真验证。

仿真实验1：假定有一个4频分量的信号x1：

x1＝sin(2*pi*300*t1)+sin(2*pi*150*t1)+sin(2*pi*250*t1)+sin(2*pi*90*t1)。

图2为原信号经过格林函数化后的时域图和频率分布图，原信号x1经过格林函数化后表示为G1。

信号G1为格林函数化后的4频叠加信号，从图2至图5中可以看出，快速傅里叶(FFT)可清晰反映G1信号的频率分布，但无法显示时间与频率的联合分布；短时傅里叶(STFT)时频图模糊，分辨率低；小波(Wavelet)时频图相对清晰正确，但是频率的聚集度不好；Wigner-Ville分布(WVD)时频图在四个频率之间存在5条交叉项干扰，干扰频率大致分别为120、170、200、230、270。图6为信号x1直接采用平滑伪Wigner-Ville分布(SPWVD)分解，没有结合格林函数的时频图，在时间轴两端会出现一些噪声干扰。而图7为采用格林函数后的时频分析，效果较好。

仿真实验2：对于信号x2＝s1+s2：

s1＝(1+0.3*cos(2*t)).*exp(-t./15).*cos(2*pi*(2.4*t+0.5*t.^1.2+0.3*sin(t)))；

s2＝cos(2*pi*(5.3*t+0.2*t.^1.3))；

t＝linspace(0,10,2048)；x1＝(1+0.2*cos(t)).*cos(2*pi.*(2*t+0.3*cos(t)))。

图8为信号x2经过格林函数化后得到的G2的时域图和快速傅里叶变换后的频域图。图9为信号G2的短时傅里叶变换(STFT)后的时频分布图，图10为信号G2的小波变换(Wavelet)时频图，图11为信号G2的Wigner-Ville分布(WVD)时频图，图12为原始信号x2的直接的Wigner-Ville分布(WVD)时频图，图13原始信号x2的直接平滑伪Wigner-Ville分布(SPWVD)时频图，图14为本发明的原始信号x2经过格林函数化后G2的SPWVD时频图。

从图8至图14可以看出，FFT只能单独观察频率分布，无法了解时间与频率的联合分布，经过格林函数化后的信号G2在多种时频分析方法的表现都不尽如意：STFT时频图十分模糊，难以分辨，Wavelet时频图较好，f＝30Hz处稍显模糊，频率分布的聚焦度较差，WVD时频图较好，但是交叉项干扰严重，出现了原信号没有的新增频率，影响了对原始信号的频率分析。如果原始信号不经过格林函数化，则从图12和图13可以看出，频率分布效果很差。只有采用本发明的图14，原始信号先经过格林函数化后，再结合SPWVD时频分析方法，最后得到的时频联合分布的效果最优。

将本方法应用于地球天然脉冲电磁场(ENPEMF)信号的时频联合分析中，可以较好的得到该信号的时间-频率的联合分布情况，有助于进一步了解地震发生前ENPEMF信号的时频分布变化，为地震的前兆信号特性研究提供依据和帮助。图15为2013年4月20日第二通道AH数据类型(420CN2AH)的信号时频分布图和快速傅里叶的频率分布图。图16为该ENPEMF数据经过格林函数化后的SPWVD时频图。