一种运载火箭推力矢量控制摇摆发动机谐振频率测试系统的制作方法

本发明涉及一种运载火箭推力矢量控制伺服机构及发动机动态特性，给出了摇摆发动机谐振频率测试方法。

背景技术：

我国运载火箭电液伺服机构摇摆液体发动机实现推力矢量控制，但火箭液体发动机通常转动惯量大、刚度低，有着严重的谐振倾向，最低仅6Hz左右。

发动机这种谐振特性，对伺服机构自身的位置闭环反馈控制回路，会产生一种负载效应，影响伺服机构动态性能和整个火箭控制系统的稳定性，必须采用针对性的控制策略进行校正补偿。而发动机结构设计复杂，其谐振特性很难仿真计算出来，只能通过试验手段测得。

技术实现要素：

本发明的目的在于提供一种摇摆发动机频率特性的测试系统，以及根据测试结果拟合出发动机动态特性数学模型的方法，使得在伺服机构上可以设计准确的控制策略参数，针对性地抑制发动机谐振。

本发明给出了一种通过试验测量、数据处理、数据拟合，得到摇摆发动机谐振频率和动态特性的测试方法

本发明的技术解决方案是：一种运载火箭推力矢量控制摇摆发动机谐振频率测试系统，包括伺服机构、角位移传感器、测试仪、地面能源；

伺服机构为内置位移传感器且一端可伸缩的机构，伺服机构一端固定，可伸缩的一端固连在发动机喷管上，地面能源为伺服机构提供动力，发动机摇摆部分通过摇摆轴与发动机机架连接，角位移传感器一端安装在发动机机架上，一端可伸缩且固定连接在发动机喷管上；测试仪发出指令控制伺服机构伸缩，伺服机构推动发动机喷管绕摇摆轴往复摇摆，角位移传感器敏感发动机喷管角度变化，并将敏感的角度信号输出至测试仪；伺服机构内置的位移传感器将伺服机构直线运动的线位移信号输出给测试仪；测试仪根据接收的角度信号和线位移信号进行比较并做减法处理，得到发动机的谐振频率。

角位移传感器安装与伺服机构安装共面，即二者均通过发动机的摇摆中心，处于同一个摇摆平面内。

测试仪发出的指令为一种或几种角度幅值下，一组不同频率的正弦电压信号。

测试仪的处理过程如下：

第一步，发出不同频率的正弦电压信号a*sin(w(i)*t)(i＝1,2,…,n)至伺服机构，其中，a为信号幅值，w(i)(i＝1,2,…,n)为信号频率，t为时间；

第二步，接收伺服机构直线运动的线位移信号u(i)*sin(w(i)*t+φu(i))(i＝1,2,…,n)和发动机角度信号y(i)*sin(w(i)*t+φy(i))(i＝1,2,…,n)；

第三步，将上述角度信号和线位移信号的比值X＝y(i)/u(i)(i＝1,2,…,n)，作为自变量代入函数A(X)＝20lgX，得到不同频率w(i)(i＝1,2,…,n)下发动机动态特性的幅值A(i)(i＝1,2,…,n)，单位为分贝；

第四步，根据Φ(i)＝φu(i)-φy(i)(i＝1,2,…,n)可得到不同频率w(i)(i＝1,2,…,n)下发动机动态特性的相角滞后Φ(i)，单位为°；

第五步，根据不同频率下发动机动态特性的相角滞后结合第三步中的结果，在二十倍对数空间下绘制发动机谐振频率特性曲线，得到发动机谐振峰频率估计值；

第六步，根据发动机谐振频率特性实测数据及曲线，将发动机等效为二阶或四阶传递函数，根据第五步中得到的谐振峰频率估计值，拟合出发动机谐振峰频率、阻尼，即可得到较准确的发动机动态特性数学模型。

本发明与现有技术相比有益效果为：

(1)本发明采用的火箭推力矢量控制摇摆发动机谐振频率测试系统，通过发送一系列正弦信号，测量相应的线位移、角位移信号，做简单数据处理，即可方便地得到准确的发动机谐振频率、等效结构阻尼比，相比传统的理论公式计算方法，不需要得到发动机的结构连接刚度和质量这两个难测参数，测试方便、结果准确。

(2)另一方面，利用传统的模态试验测量发动机固有特性，激励较低，不一定能准确全面的激发出发动机的全部谐振特性。本方法则可以准确设定输入正弦激励信号的强度(即正弦幅值)，实现有效测量。

(3)以往运载火箭伺服机构测量出角位移信号后，得到发动机角位移谐振频率Wc。根据液压通用公式计算得到伺服机构液压固有频率Wh，代入公式1/Wh²+1/Wr²＝1/Wc²，解算出发动机谐振频率Wr。计算结果不够精确，此方法不适用于四阶的发动机谐振特性。而本发明采用的测试方法对典型的二阶、四阶发动机谐振特性均适用。

附图说明

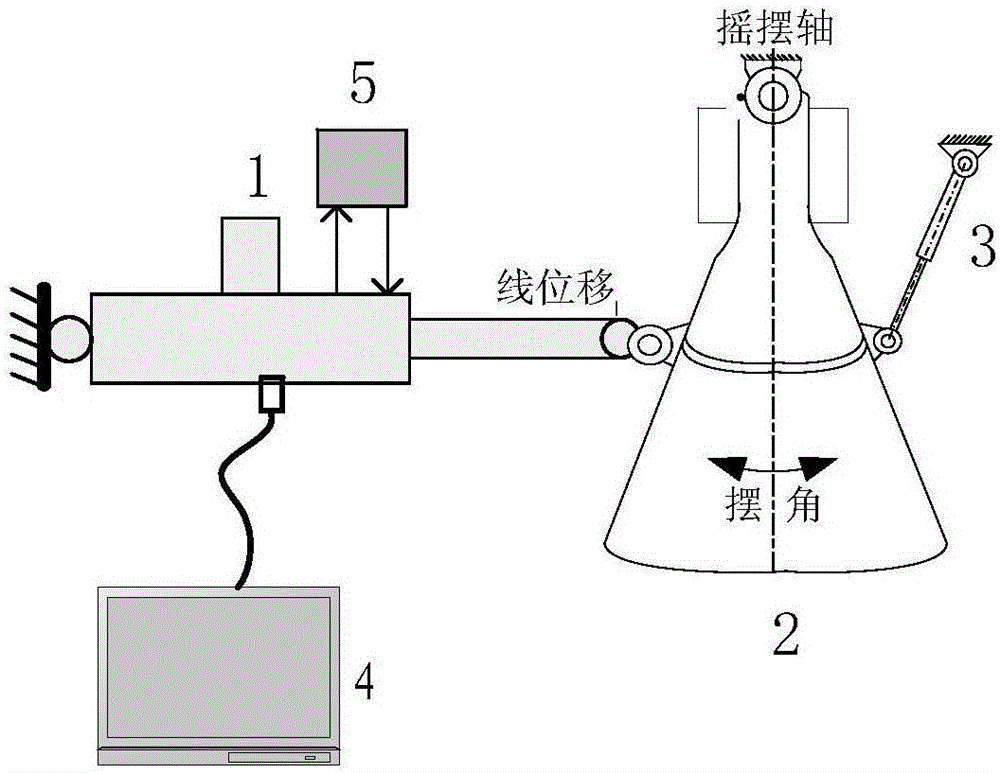
图1为本发明系统示意图；

图2为本发明单谐振点发动机负载下的系统模型；

图3为本发明双谐振点发动机负载下的系统模型；

图4为本发明双谐振点发动机实测频率特性曲线及拟合结果。

具体实施方式

下面结合附图及实例对本发明做详细说明。

如图1所示，本发明系统包括伺服机构1、角位移传感器3、测试仪4、地面能源5；伺服机构1为内置位移传感器且一端可伸缩的机构，伺服机构1一端固定在发动机2机架上，可伸缩的一端固连在发动机2喷管上，地面能源5为伺服机构1供电，发动机摇摆部分上端通过摇摆轴连接，角位移传感器3一端安装在发动机2机架上，一端可伸缩且固定连接在发动机喷管上，与伺服机构共面、通过同一摇摆中心；测试仪4发出指令控制伺服机构伸缩，伺服机构推动发动机喷管绕摇摆轴往复摇摆，角位移传感器3敏感发动机喷管角度变化，并将敏感的角度信号输出至测试仪4；伺服机构1内置的位移传感器将伺服机构直线运动的线位移信号输出给测试仪4；本发明以测量得到的伺服机构直线位移作为输入，发动机的摇摆角位移作为输出，两者比较即可得到摇摆发动机的频域动态特性测试数据，并根据其辨识发动机的特性参数。

伺服机构与单谐振点发动机联合简化控制模型如图2。

由测试仪4发出某一种或某几种角度幅值下，一组不同频率的正弦电压信号a*sin(w(i)*t)(a为信号幅值，i＝1,2,3…,n，t为时间)，控制伺服机构1往复运动的幅值、频率，通过内置的位移传感器测量伺服机构1伸缩端位置并反馈回测试仪4，定义线位移信号为u(t)。

通过伺服机构1的直线往复运动，推动发动机2摇摆，通过安装在发动机2上的角位移传感器3测量发动机2实际的摆角并反馈回测试仪4，定义发动机角位移为y(t)。根据图2，线位移信号u(t)为发动机2摇摆的输入信号，角位移信号y(t)为发动机2摇摆的输出信号，利用测试仪4对这两个信号进行比较和数据处理，具体如下：

由图2，发动机负载特性G(t)＝y(t)/u(t)。代入不同频率的正弦电压信号a*sin(w(i)*t)(a为信号幅值，w(i)(i＝1,2,…,n)为信号频率，t为时间)，得到伺服机构1线位移u(i)*sin(w(i)*t+φu(i))(i＝1,2,…,n)和发动机角位移y(i)*sin(w(i)*t+φy(i))(i＝1,2,…,n)。将上述角度信号和线位移信号的比值X＝y(i)/u(i)(i＝1,2,…,n)，作为自变量代入函数A(X)＝20lgX，得到不同频率w(i)(i＝1,2,…,n)下发动机动态特性的幅值A(i)(i＝1,2,…,n)，单位为分贝。根据Φ(i)＝φu(i)-φy(i)(i＝1,2,…,n)可得到不同频率w(i)(i＝1,2,…,n)下发动机动态特性的相角滞后Φ，单位为°。利用matlab在二十倍程对数空间内画出发动机动态特性的幅值A(i)和相角(i)相对于信号频率w(i)(i＝1,2,…,n)的曲线。可得到发动机谐振峰频率估计值；该估计值在后续进行数据拟合时，可用于发动机谐振参数初值确定及参数调整范围。

上述a*sin(w(i)*t)为正弦电压信号，u(i)*sin(w(i)*t+φu(i))为线位移信号，y(i)*sin(w(i)*t+φy(i))为角位移信号，φu(i)、φy(i)为相对于正弦电压信号的相角滞后。

另一方面，不同类型发动机其谐振频率特性有所不同。国内多型发动机谐振频率特性测试结果，通常表现为一个或两个谐振峰，可将发动机控制模型等效为二阶传递函数或四阶传递函数。拟合出发动机谐振峰频率、阻尼，即可得到较准确的发动机动态特性数学模型。

二阶传递函数：

四阶传递函数：

得到ωr1为发动机第一个谐振峰频率、ωr2为发动机第二个谐振峰频率，ζr1为发动机第一个谐振峰等效结构阻尼比、ζr2第二个谐振峰等效结构阻尼比。ωr3为发动机零点频率，ζr3为发动机零点等效结构阻尼比。

以图3所示发动机双谐振点频率特性曲线为例，将两处谐振尖峰和一处凹口尖峰频率点作为ωr1、ωr2、ωr3，根据谐振峰最大分贝值y＝20lg(1/(2*ζ))，计算出ζr1、ζr2值，根据凹口尖峰最大分贝值y＝20lg(2*ζ)，计算出ζr3值,代入发动机的四阶传递函数模型，即可得到准确的发动机双谐振点频率特性数学模型。

类似的，若发动机频率特性曲线为单谐振点。可同样得出ωr、ζr值，代入发动机的二阶传递函数模型，即可得到准确的发动机单谐振点频率特性数学模型。

根据实测数据拟合得到的谐振峰频率、等效结构阻尼比，可以较准确的反映发动机动态特性特别是谐振峰特性，为准确抑制发动机谐振，设计最佳控制策略参数，提供了数据支撑。

本发明未详细说明部分属于本领域技术人员公知常识。