一种内流道阻力测量方法与流程

本发明涉及一种内流道阻力测量方法，属于风洞试验领域。

背景技术：

吸气式高超声速飞行器既能实现全球快速到达，又可低成本进入空间，是当前国内外高超声速领域的研究热点之一。这种以超燃冲压发动机为动力的飞行器普遍采用机体/推进一体化设计(如X-43A、X-51A)，存在强烈的内外流干扰，使得内流道的流动特性和气动特性对飞行器气动特性产生重要了影响，从而对通气模型内流道阻力的精确测量提出了迫切需求，以解决飞行器推阻特性分析所面临内流道阻力扣除难题。

目前，风洞试验获得吸气式高超声速飞行器通气模型内流道阻力的方法有两种：一种是通过总静压法测量通气模型内流道进出口气流动量差的方法获得；另一种则是采用测力天平直接测量内流道气动力特性。其中，总静压法需要在内流道出口安装较密集的总压测量管，属于侵入式测量方法，存在流场干扰问题，同时测量准确性严重依赖于吸气式高超声速飞行器内流道进出口流场的不均匀性；测力天平直接测量法需要将内外流道从物理上解耦、剖分内外流两个独立部件、实现内流道部件的天平安装，不仅存在流道破坏问题，而且存在内外流道解耦产生的缝隙密封难题，同时还要考虑密封介质及缝隙漏流的干扰程度和修正问题。因此，迫切需要发展一种非侵入式测量方法，克服流场分布、流场干扰测力天平自身的影响，是本领域亟待解决的技术问题。

技术实现要素：

本发明的目的在于克服现有技术的不足，提供一种内流道阻力测量方法，保证在流场无干扰、流道无破坏条件下精确测得内流道的阻力，为评估内流道阻力在整个飞行器总阻力的贡献提供了一种新方法。

本发明目的通过如下技术方案予以实现：

一种内流道阻力测量方法，包括如下步骤：

(1)根据风洞试验气体确定测量内流道阻力的目标气体组分，选择该目标气体组分对应的吸收谱线1和2构成谱线对；

(2)建立基于可调谐半导体激光吸收光谱技术的内流道阻力测量系统；

(3)采用内流道阻力测量系统测量进口处和出口处目标气体组分吸收谱线1和2的积分吸收率，再由Beer-Lambert吸收定律确定的“积分吸收率之比与温度之间的单值函数关系”计算内流道进口处和出口处气流的静温；

(4)使内流道进、出口截面处气流的总温与风洞来流总温一致，计算内流道进口处和出口处气流的马赫数Ma；

(5)根据Beer-Lambert吸收定律，计算内流道进口处和出口处目标气体组分的分压；

(6)根据道尔顿分压定律，计算内流道进口处和出口处气流的静压p；

(7)根据理想气体状态方程，计算内流道进口处和出口处气流的动量差ΔP；

(8)根据动量定理，获得内流道阻力D。

优选的，风洞试验气体为空气，目标气体为氧气，选取吸收谱线1的中心频率为13100.822320cm^-1，吸收谱线2的中心频率为213041.125130cm^-1构成谱线对。

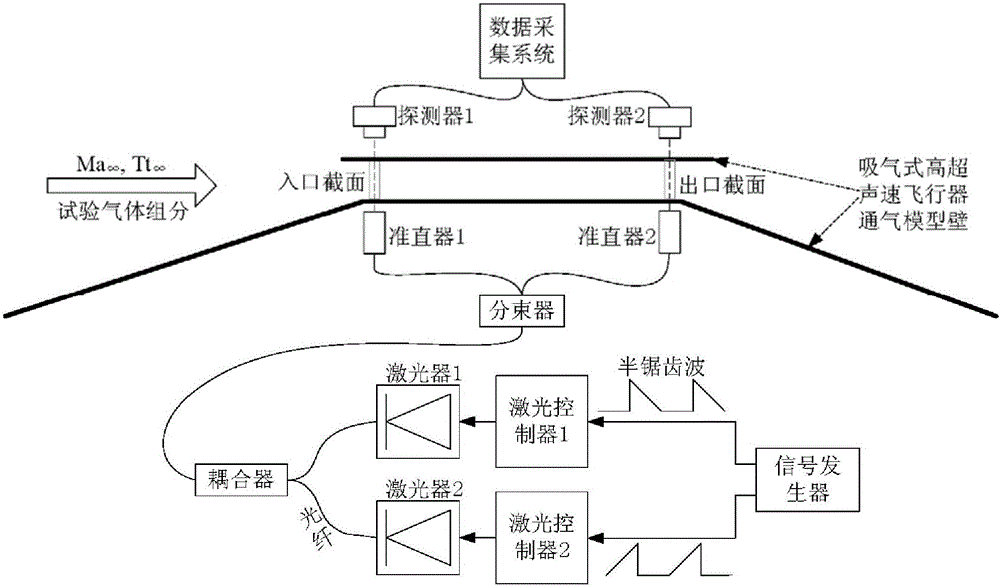
优选的，内流道阻力测量系统包括信号发生器、两台激光控制器、两台激光器、单模光纤、耦合器、分束器、第一准直器、第二准直器、第一探测器、第二探测器和数据采集系统；

信号发生器生成两路相位相差180°的半锯齿波信号，分别发送到两台激光控制器，两台激光控制器各控制一台激光器，使两台激光器的中心频率分别为吸收谱线1的中心频率和吸收谱线2的中心频率，两台激光器产生两束激光，两束激光经耦合器耦合到一根单模光纤，再由分束器分成两束光，其中一束光光传输至内流道进口处的第一准直器，穿过内流道进口截面气流后，由布置内流道进口处的第一探测器接收，并转变成电信号，输入到数据采集系统，获得进口处吸收谱线1和2的原始吸收强度信号；另一束光传输至布置内流道出口处第二准直器，穿过内流道出口截面气流后，由布置内流道出口处的第二探测器接收，并转变成电信号，输入到数据采集系统，获得出口处吸收谱线1和2的原始吸收强度信号；数据采集系统分别绘制进口处和出口处吸收谱线1和2的吸收强度随频率变化的分布曲线，通过积分整个频率上的吸收强度分别获得进口处吸收谱线1和2的积分吸收率Λ_1,in和Λ_1,in和出口处吸收谱线1和2的积分吸收率Λ_1,ex和Λ_2,ex。

优选的，步骤(3)中计算内流道进口处和出口处气流的静温T_in和T_ex的具体方法为：

$T_{in}=\frac{\frac{hc}{k}(E_2^{\′\′}-E_1^{\′\′})}{ln\left(\frac{{\mathrm{\Λ}}_{1,in}}{{\mathrm{\Λ}}_{2,in}}\right)+ln\frac{S_2\left(T_0\right)}{S_1\left(T_0\right)}+\frac{hc}{k}\frac{E_2^{\′\′}-E_1^{\′\′}}{T_0}},$

$T_{ex}=\frac{\frac{hc}{k}(E_2^{\′\′}-E_1^{\′\′})}{ln\left(\frac{{\mathrm{\Λ}}_{1,ex}}{{\mathrm{\Λ}}_{2,ex}}\right)+ln\frac{S_2\left(T_0\right)}{S_1\left(T_0\right)}+\frac{hc}{k}\frac{E_2^{\′\′}-E_1^{\′\′}}{T_0}}$

S₁(T₀)和S₂(T₀)分别为吸收谱线1和2在参考温度T₀下的谱线强度，和分别为吸收谱线1和2在低能级下的能量，h为普朗克常数，c为光在真空中的传播速度，k为玻尔兹曼常数。

优选的，步骤(7)中计算内流道进出口气流的动量差ΔP的具体放方法为：

$\mathrm{\Δ}P=\[(\mathrm{\γ}\·{{\mathrm{Ma}}_{in}}^2+1)p_{in}\·A_{in}\]-\[(\mathrm{\γ}\·{{\mathrm{Ma}}_{ex}}^2+1)p_{ex}\·A_{ex}\]$

其中A_in和A_ex分别为内流道进口处和出口处的截面面积，γ为风洞试验气体比热比，p_in和p_ex分别为内流道进口处和出口气流的静压，Ma_in和Ma_ex分别为内流道进口处和出口处气流的马赫数。

优选的，所述内流道的形状为以圆形、方形或矩形为截面形状的等直或扩张管道，或者为圆形转方形变截面形状的弯曲管道。

本发明与现有技术相比具有如下优点：

(1)本发明采用非侵入式测量，激光穿过待测流场获得吸收信息而不影响流场分布，解决了测量过程中总静压法的流场干扰问题和测力天平测量法的流道破坏和缝隙密封等问题。

(2)本发明采用光程上的线积分测量，测得的气流参数如温度、压力为沿着光程上气流的平均值，与传统的点式测量相比，可有效改善流场不均匀导致的测量精度严重依赖于测点数量问题。

(3)本发明可监测内流道的流动状态，利用测得的气流静温和静压及理想气体状态方程，可得内流道捕获的流量，与理想捕获流量比较，用途更广，还可用于判断内流道存在缩尺情况的流动相似性。

(4)随着TDLAS设备的小型化进展，可将设备置于内流道的固体结构内部；若在X-51A等吸气式高超声速飞行器的气动试验时采用这种技术，还能在同一车次测得内流道阻力的同时获得飞行器外流气动数据。

(5)本发明不仅适合测量以超燃冲压发动机为动力的吸气式高超声速飞行器的内流道阻力，还可以测量所有以空气为的可压流动的内通道阻力。

附图说明

图1为本发明内流道阻力计算方法示意图；

图2为可调谐半导体激光吸收光谱技术测量系统组成示意图。

具体实施方式

本发明提出了一种基于新近发展起来的可调谐半导体激光吸收光谱技术来测量吸气式高超声速飞行器通气模型内流道阻力的方法。该方法首先利用可调谐半导体激光吸收光谱技术(Tunable Diode Laser Absorption Spectroscopy,TDLAS)的窄线宽半导体激光器光源，扫描选定目标气体组分的吸收谱线信息，实现对内流道进出口气流的静温及目标气体组分的分压进行测量，然后根据能量守恒和风洞气流总温参数、由空气动力学的总静温关系式计算出内流道进出口气流的马赫数，同时由道尔顿分压定律和和目标气体组分在试验气体中的摩尔百分比、计算出内流道进出口气流的马赫数和静压，继而可计算出内流道进出口动量差、获得内流道阻力，有效解决了现有技术的不足。

以某常规高超声速风洞的吸气式高超声速飞行器通气模型的内阻测量试验为例，风洞试验气体为空气，主要组分为氧分子(摩尔百分比)和氮分子比热比为γ，气体常数为R_空气；试验来流参数分别为马赫数Ma_∞＝6、总温Tt_∞＝464K、总压Pt_∞＝2MPa；具体实施步骤如下：

(1)由上述风洞运行参数，确定氧分子(O₂)作为可调谐半导体激光吸收光谱技术测量的目标气体组分；综合吸收强度、温度灵敏度和邻近谱线干扰等因素的影响，查询光谱数据库如HITRAN2004，选取吸收谱线的中心频率为13100.822320cm^-1(吸收谱线1)和13041.125130cm^-1(吸收谱线2)构成谱线对。

(2)建立内流道的可调谐半导体激光吸收光谱技术的测量系统，包括信号发生器、激光控制器、激光器、光纤、耦合器、分束器、准直器、探测器、数据采集系统，其特征在于：信号发生器的标准脉冲锯齿波经方波调制产生两路相位相差180°的半锯齿波信号，送入两台激光控制器产生两路扫描信号，接入两台窄带宽激光器产生两束激光，经耦合器耦合到一根单模光纤中以实现双吸收线分时扫描同一待测区域，再由分束器分成两束光，其中一束光经光纤传输至布置内流道进口处的准直器，穿过内流道进口截面气流后，由布置内流道进口处的探测器接收并转变成电信号，输入到数据采集系统；另一束光经光纤传输至布置内流道出口处准直器，穿过内流道出口截面气流后，由布置内流道出口处探测器接收并转变成电信号，输入到数据采集系统；所述内流道的形状存在多样性，可为圆形、方形、矩形等截面形状的等直或扩张管道，也可为圆转方等变截面形状的弯曲管道；所述的准直器与探测器成对布置在内流道进出口截面两侧；所述两台激光器的中心频率分别为13100.822cm^-1和13041.125cm^-1。数据采集系统分别绘制进口处和出口处吸收谱线1和2的吸收强度随频率变化的分布曲线，通过积分整个频率上的吸收强度分别获得进口处吸收谱线1和2的积分吸收率Λ_1,in和Λ_2,in和出口处吸收谱线1和2的积分吸收率Λ_1,ex和Λ_2,ex。

(3)基于Beer-Lambert吸收定律，采用双线测温法，测量内流道进出口处气流的静温，具体步骤：由所述步骤(2)建立的测量系统测得目标气体组分(O₂)吸收谱线1和2的吸收光谱数据即谱线1和2的吸收强度随频率分布曲线，通过积分整个频率上的吸收强度分别获得谱线1和2的积分吸收率，再根据Beer-Lambert吸收定律确定的“积分吸收率之比与温度之间的单值函数关系”反演出内流道进、出口气流的静温，进、出口处气流的静温T_in和T_ex计算公式如下：

$T_{in}=\frac{\frac{hc}{k}(E_2^{\′\′}-E_1^{\′\′})}{ln\left(\frac{{\mathrm{\Λ}}_{1,in}}{{\mathrm{\Λ}}_{2,in}}\right)+ln\frac{S_2\left(T_0\right)}{S_1\left(T_0\right)}+\frac{hc}{k}\frac{E_2^{\′\′}-E_1^{\′\′}}{T_0}},$

$T_{ex}=\frac{\frac{hc}{k}(E_2^{\′\′}-E_1^{\′\′})}{ln\left(\frac{{\mathrm{\Λ}}_{1,ex}}{{\mathrm{\Λ}}_{2,ex}}\right)+ln\frac{S_2\left(T_0\right)}{S_1\left(T_0\right)}+\frac{hc}{k}\frac{E_2^{\′\′}-E_1^{\′\′}}{T_0}}$

其中S₁(T₀)和S₂(T₀)分别为吸收谱线1和2在参考温度T₀＝296K下的谱线强度，E″₁和E″₂分别为吸收谱线1和2在低能级下的能量，查询光谱数据库HITRAN2004可得：S₁(T₀)＝1.385×10^-24cm^-1/(molecule·cm^-2)、E″₂＝664.2595cm^-1和S₂(T₀)＝7.153×10^-24cm^-1/(molecule·cm^-2)、E″₁＝79.6070cm^-1；h为普朗克常数，c为光在真空中的传播速度，k为玻尔兹曼常数。

(4)考虑到常规高超声速风洞中气流经过模型损失的能量微乎其微，可认为通气模型内流道进出口截面处气流的总温与风洞来流总温Tt_∞一致，再由所述步骤(3)得到的静温，根据总静温关系式，计算内流道进、出口处气流的马赫数Ma_in和Ma_ex，公式如下：

${\mathrm{Ma}}_{in}=\sqrt{\frac{2(\frac{{\mathrm{Tt}}_{\mathrm{\∞}}}{T_{in}}-1)}{\mathrm{\γ}-1}}$

${\mathrm{Ma}}_{ex}=\sqrt{\frac{2(\frac{{\mathrm{Tt}}_{\mathrm{\∞}}}{T_{ex}}-1)}{\mathrm{\γ}-1}}.$

(5)基于Beer-Lambert吸收定律、试验测得的吸收谱线的积分吸收率及所述步骤(3)所得的静温，计算内流道进、出口处目标气体组分(O₂)的分压和计算公式如下：

$p_{O_2,in}=\frac{{\mathrm{\Λ}}_{1,in}}{S_1\left(T_{in}\right)\·L_{in}},$

$p_{O_2,in}=\frac{{\mathrm{\Λ}}_{1,ex}}{S_1\left(T_{ex}\right)\·L_{ex}}$

其中S₁(T_in)、S₁(T_ex)分别为吸收谱线1在所述步骤(3)测得的进、出口处气流静温T_in和T_ex下的谱线强度，通过所述步骤(3)得到的静温查询光谱数据库获得，L_in、L_ex分别为进、出口截面光程长度。

(6)由目标气体组分在试验气体中的摩尔百分比和所述步骤(5)所得的内流道进、出口截面处目标气体组分(O₂)的分压，根据道尔顿分压定律，计算内流道进、出口气流的静压p_in和p_ex，具体计算公式如下：

$p_{in}=p_{O_2,in}/{\mathrm{\χ}}_{O_2},$

$p_{ex}=p_{O_2,ex}/{\mathrm{\χ}}_{O_2}.$

(7)由所述步骤(4)所得的内流道进、出口气流马赫数和所述步骤(6)所得的内流道进、出口气流静压，根据理想气体状态方程，可得内流道进出口气流的动量差ΔP，公式如下：

ΔP＝[(γ·Ma_in²+1)p_in·A_in]-[(γ·Ma_ex²+1)p_ex·A_ex]

A_in、A_ex分别为内流道进、出口处的截面面积。

(8)由所述步骤(7)所得的内流道进出口气流动量差，结合动量定理，即可获得内流道阻力D，公式如下：

D＝ΔP。

以上所述，仅为本发明最佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到的变化或替换，都应涵盖在本发明的保护范围之内。

本发明说明书中未作详细描述的内容属于本领域专业技术人员的公知技术。