斜拉索索力测试方法与流程

本发明属斜拉桥技术领域，具体涉及一种斜拉索索力测试方法。

背景技术：

目前常用的索力测试方法主要有以下几种，如压力传感器法、磁通量法、振动频率法和千斤顶法等。

对运营中的斜拉桥，振动频率法和磁通量法是最主要的索力测试方法，其余的方法一般仅用于施工过程中斜拉索的索力测试。磁通量法由于测试费用昂贵而采用较少；振动频率法因其操作方便、快捷，测试费用低而在工程中广泛应用，几乎是目前成桥索力测试的唯一方法，但其测试精度受到斜拉索边界条件（比如设有减振器的情况）、垂度以及抗弯刚度等因素的影响较大，测试结果往往不够精准。

技术实现要素：

本发明要解决的技术问题是针对上述现有技术的不足，提供一种斜拉索索力测试方法，旨在提供一种操作简单、测试精度较高、测试费用相对低廉的斜拉索索力测试技术方案。

为解决上述技术问题，本发明采取的技术方案是：一种斜拉索索力测试方法，通过测量斜拉索中一索段的垂度来得到整个斜拉索的索力，包括以下步骤 ：

步骤一：在斜拉索上任取一不包括两端锚点与减振器支点的中间索段，所述索段线形为曲线OME，对应弦长为OE，M点为OME的中点，L为斜拉索对应弦长OE，f为所述索段垂直于OE的最大垂度，索段的倾角为α；测量索段垂度f、倾角α、弦长L；

步骤二：建立所述索段索力与垂度的关系，利用所述关系计算索段的平均索力。

采用上述技术方案所产生的有益效果在于：

本发明的斜拉索索力测试方法所基于的理论基础简单，具有操作比较简单方便、精度较高、所需的设备可重复使用、测试费用经济的特点。本发明为斜拉索索力的测定，特别是成桥索力的测定提供了一种准确可靠的方法。

附图说明

图1是本发明实施例中索段模型示意图。

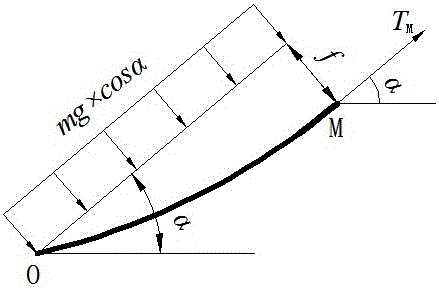
图2是图1中取出的力学分析隔离体示意图。

具体实施方式

为了使本发明所要解决的技术问题、技术方案及有益效果更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。

斜拉索在索力和自重作用下会产生“垂度”，该垂度的大小主要与斜拉索的长度、单位长度重量、倾角以及索力的大小有关。在斜拉索边界条件和外界温度一定的情况下，其索力与垂度有确定的对应关系，通过该对应关系可以测定索力的大小。由于斜拉索本身的抗弯刚度相对很低，在离开斜拉索锚固点或减振器支点一定距离后，斜拉索中间任意一段的垂度与锚固点或减振器支点等边界条件几乎无关，该索段的两端可认为是铰接边界条件，可以通过测定这一段的拉索垂度来求出索力大小。将利用测量斜拉索中某一索段的垂度来测定其索力的方法定义为“垂度法”。本发明的实施例就是一种基于垂度法的斜拉索索力测试方法。

一种斜拉索索力测试方法，包括以下步骤 ：

步骤一：如图1所示，在斜拉索上任取一不包括两端锚点及减振器支点的中间索段，所述索段线形为曲线OME，对应弦长为OE，M点为OME的中点，L为斜拉索对应弦长OE，f为所述索段垂直于OE的最大垂度，索段的倾角为α；测量索段垂度f、倾角α、弦长L。对于索段的最大垂度的得到办法可采用全站仪测量O、M和E的空间坐标后计算得到；当斜拉索的垂跨比（垂度f与跨度L的比值）较小（如1/100）时，索段曲线可认为是二次抛物线或者悬链线，垂度近似等于弦中点到索段中点的距离长度，且索段近似关于两中点的连线对称。

步骤二：推导索段的垂度与索力关系的公式，利用所述公式计算所述索段的平均索力。

上述斜拉索索力测试方法的步骤一和步骤二并没有明显的先后顺序，颠倒步骤一和步骤二的顺序不会影响本方法的测试效率和精度，应当理解，颠倒步骤一和步骤二的顺序仍在本发明的的保护范围内。本实施例计算方法基于的理论基础简单，具有操作简单方便、精度较高、所需的设备可重复使用、测试费用经济的特点。

作为优选，所述垂度与索力关系的公式计算方法为：

假定所述索段的索形为抛物线且两端铰接，忽略拉索本身弯曲刚度的影响，设单位长度拉索质量为m（该值可采用设计的已知值或后续测量值），重力加速度为g，在垂跨比很小的情况下，单位长度的索重mg分解时可假定索形无限接近弦向直线，索重mg则分解成垂直于弦向直线的mgcosα和平行于弦向直线的mgsinα；

如图2所示，对铰接点O取矩可得索形为抛物线时最大垂度f与平均索力T_M的简化公式为：

式中T_M为斜拉索平均索力；m为单位长度斜拉索质量；g为重力加速度，以上式中各参数均选取国际标准单位进行计算。

在步骤一测得索段垂度f、倾角α、弦长L后，即可利用公式（1）计算求出选取索段的平均索力，由于斜拉索各处索力不同的原因是斜拉索自重的影响，而斜拉索自重与索力相比很小，就可近似认为斜拉索的各处索力一样，因此上述计算出的选取索段的平均索力就可以认为是整个斜拉索的平均索力。本实施例采用解析法确定垂度与索力关系的公式，理论基础简单易于理解，易于操作计算。

作为优选，若期获得更精确的索力，则可按T=T_M±mglsinα进行修正，得到修正后的整个斜拉索的平均索力T，其中l为所选取索段中点到整个斜拉索的中点的距离，所选取索段中点在整个斜拉索的中点上方时取负号，下方时取正号。

作为优选，索力与垂度关系还可以通过采用有限元方法建立具体斜拉索计算模型，模拟计算所述斜拉索不同索力对应的垂度，进而拟合出其索力与垂度的关系为公式（2）

上述方法可利用有限元软件考虑拉索的大变形效应和应力刚化效应，计算结果与实际非常接近并且可以实现参数化编程计算。为了计算索力与垂度的关系，所编写的程序需要输入索的设计索力T₀、弦长L、拉索倾角α、索的有效面积（钢丝或钢绞线截面有效面积之和）、索力和单位长度索的质量m（这些值为设计已知值）。编写程序使索力在某个区间变化，如0.2T₀~2.0T₀，第一次计算0.2T₀时对应最大垂度，然后每次增加0.05T₀直至2.0T₀，这样总共计算37次。这样对特定的斜拉索可得到37组索力-垂度数据，根据这些数据可得到索力-垂度关系曲线，进而拟合出其索力与垂度的关系为公式。需要指出，上述的公式（2）T_M=F(f)是利用有限元法拟合的公式，与具体的斜拉索有关，并非是一个固定的公式。

作为优选，通过全站仪测得所述索段两端点O和E及中点M截面中心的空间坐标，然后根据所测得的三点空间坐标计算出索段的垂度f、倾角α、弦长L。通过全站仪测量计算垂度f、倾角α、弦长L成本相对低廉，精度较高。

作为优选，所述在斜拉索上选取索段不宜靠近两边的锚点以及减振器支点，因为受边界条件影响较大，宜远离两端的锚点以及减振器支点5m以上；选取的中间索段不宜太短，应使该索段垂度大于20mm为宜，以便在使用普通全站仪的测量误差为1mm时，保证计算出的索力误差小于5%。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。