一种基于floyd算法的无人机路径规划方法与流程

本发明涉及一种无人机路径规划方法，尤其涉及一种基于floyd算法的无人机路径规划方法。

背景技术：

随着科技的发展，无人机被广泛地应用到了各个领域，如军事、农业、建筑行业等。无人机包含了多种技术，如协同控制，编队等。繁重的任务、变化的多机协同战术应用，有效组织与科学管理无人机完成指定的任务迫在眉睫。基于此，路径动态规划与无人机而言是一项举足轻重的技术，必不可少。无人机路径的动态规划既可以提高效率又能保证安全性，是无人机的一项关键技术。

无人机在飞行过程中，可能会有无数条路径可以到达目标节点，怎么选择最佳路径到达目标节点是动态路径规划的目的。在规划过程中需要考虑障碍物，障碍物越是密集，则需要的中间节点也就越多，计算复杂度就会越高。寻找最佳飞行航线，确定该航线上对载荷设备的控制策略是无人机路径规划的目的，从而使无人机在飞行安全确保的前提下，发挥载荷设备的作用，完成各项任务。经过动态规划，无人机可以从根节点通过最短路径到达终端节点，节省了时间和资源。

就目前而言，我国对于无人机的路径动态规划探索还处于初级阶段，很多技术尚未成熟。目前也存在一些路径规划算法，如dijistra算法和HOCAOGLU算法等，但是存在计算复杂度高，效率低等问题，。

技术实现要素：

有鉴于此，本发明的目的是提供一种基于floyd算法的无人机路径规划方法，该算法不仅中间节点选取方法简单而且效率高。

本发明通过以下技术手段解决上述技术问题：

一种基于floyd算法的无人机路径规划方法，其特征在于，包括如下步骤：

第一步，确定坐标，基于地球中心坐标系，标注出障碍物以及初始点和目标节点的位置，分别设为Z(x,y),S(x,y),G(x,y)，从而构成任务地图的初始形态；

建立地球中心坐标系，采用地图工具标注出初始点的根节点坐标为S(x,y),目标节点为G(x,y),并标注出障碍物坐标Z(x,y),建立起三个节点的坐标，为图的组成提供基础节点；搭建结构体，所述结构体包括LinkNode和Node，其中结构体变量包括：邻接的结点在数组中的编号vex，指向下一个节点next，节点所存数据data，列表头节点head，并以此来建立图；

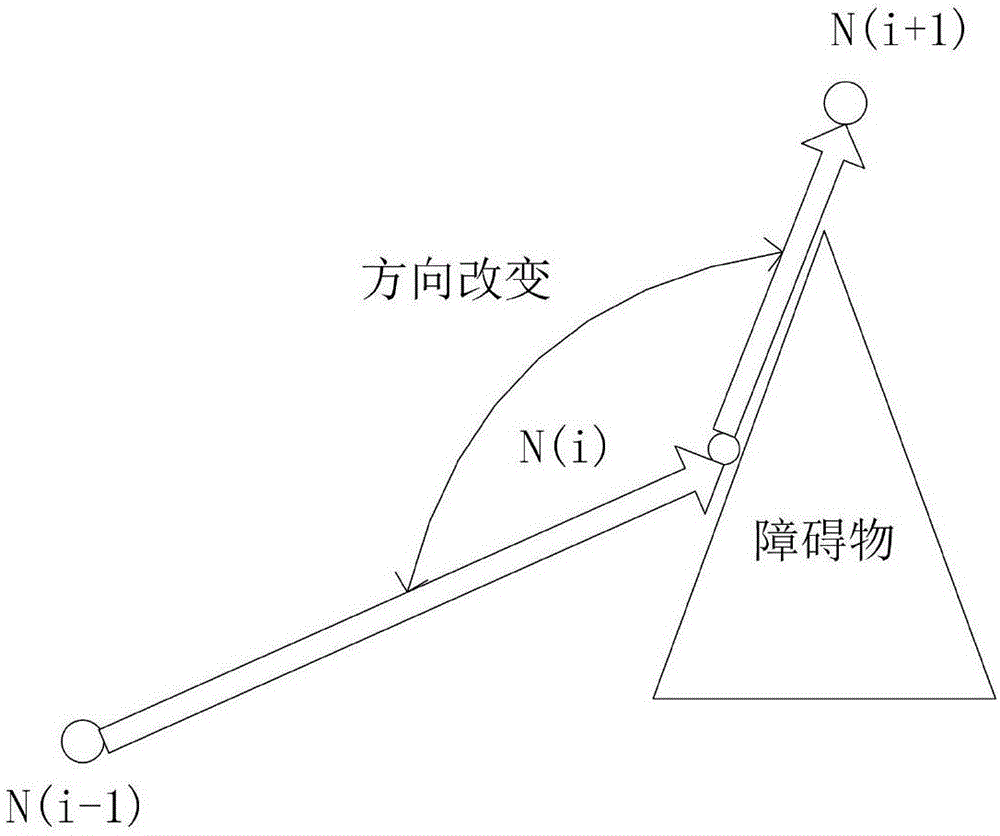
第二步，选择中间节点，以无人机飞行方向的转折点及航向改变点作为为中间节点，改变航向即是无法进行两点之间直线飞行时，遇到障碍物时会发生方向的改变，将每一个方向的改变点作为一个中间节点，结合上述障碍物以及初始点和目标节点构成图；

初始化根节点S(x,y)航向角θ₀，比较点i处的航向角θ_i与前一航向角θ_i-1，判断是否相等，若相等，则i点不能选择为中间节点，若不相等则i就是其中一个中间节点；

第三步，最佳路径选择，从图的带权邻接矩阵A＝[a(i,j)]n×n开始，递归地进行n次更新，即由矩阵D(0)＝A，按一个公式，构造出矩阵D(1)；又用同样地公式由D(1)构造出D(2)；……；最后又用同样的公式由D(n-1)构造出矩阵D(n)，矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度，称D(n)为图的距离矩阵，同时引入一个后继节点矩阵path来记录两点间的最短路径，该最短路径就是无人机的最佳航线；

采用floyd算法从初始点到中间节点的选择到目标节点，将初始点作为根节点，从根节点到目标节点进行遍历，组建成一个图，采用floyd方法进行最佳路径规划，包含变量节点个数vertexnum，权重weight，将每次算法计算得到的路径都存放path[]中，通过权重矩阵和路径矩阵的矩阵运算可以算出最佳路线，得到从根节点到目标节点的最短路径。

作为本方案的进一步改进，所述障碍物使指利用检测仪检测到的位于从初始点到终端节点路径上的的阻碍物体。

作为本方案的进一步改进，所述采用floyd方法进行最佳路径规划包括以下步骤：

开始，遍历所述图中的每一对顶点，找出各个节点间的距离用权值代替，没有边相连的，则权为无限大；

判断，对于每对顶点U，V看是否存在W点使得点U到点W，点W到点V比已知的路径更短；

如果存在点W使得点U到点W，点W到点V比已知的路径更短则更新权重矩阵最短路径；

重复上述步骤，直至找到初始点到终端节点的最短路径。

作为本方案的进一步改进，所述第二步骤中某一区域内存在多个中间节点，其中最优的中间节点选择方法如下：确定点N(i)，建立直角坐标系，点N(i-1)通过x轴对称成为N’(i-1)，点N’(i-1)与点N(i+1)的连线与纵坐标交点即为最优中间节点N(i)。

本发明的有益效果：

1.最短路径计算方法效率高，Floyd算法适用于APSP(All Pairs Shortest Paths，多源最短路径)，是一种动态规划算法，稠密图效果最佳，边权可正可负。此算法简单有效，由于三重循环结构紧凑，对于稠密图，效率要高于执行|V|次Dijkstra算法，也要高于执行V次SPFA算法，同时Floyd算法容易理解，代码易写。

2.中间节点选取方法简单有效，由无人机方向的改变来确定中间节点的选取，既简单也可保证中间节点选取的合理性。无论是处于障碍物还是两点之间不可直达，都会导致航向的变化产生中间节点。直接由方向来决定，无需考虑障碍物的位置以及其他因素，减少了中间节点确立的复杂度。航向改变证明由原本航向在此点到终结点不可达，由此将此点设为中点节点也具有合理性。

3.模块化强，具有相对独立性，中间节点的选取方法不依赖于初始位置和最短路径计算，因此中间节点的选取可最短路径计算可模块化，可移植，可改变，较独立。

附图说明

图1是本发明的步骤流程图；

图2是floyd算法流程图；

图3是中间节点选取示意图；

图4是路径规划示意图；

图5是最优中间节点算法流程图:

图6是中间节点确定示意图。

具体实施方式

以下将结合附图对本发明进行详细说明：

如图1至图6所示：

一种基于floyd算法的无人机路径规划方法，本方法是基于floyd的动态路径规划。从图的带权邻接矩阵A＝[a(i,j)]n×n开始，递归地进行n次更新，即由矩阵D(0)＝A，按一个公式，构造出矩阵D(1)；又用同样地公式由D(1)构造出D(2)；……；最后又用同样的公式由D(n-1)构造出矩阵D(n)。矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度，称D(n)为图的距离矩阵，同时还可引入一个后继节点矩阵path来记录两点间的最短路径。通过此种方法找出始终节点间的最短路径。

本方法分为三个部分：确定坐标、中间节点的确定、最佳路径的选择。

确定坐标：

确定坐标部分主要基于地球中心坐标系，标注出障碍物以及出发节点和目标节点的位置，分别设为Z(x,y),S(x,y),G(x,y)，从而构成任务地图的初始形态。完成任务地图的初始化有利于后面中间节点的确定以及为最佳路线奠定了计算基础。确定坐标部分是最基层也是尤为重要的一部分，确立了无人机飞行的初始位置和大概航线。

确定中间节点：

初始节点和终端节点是已经确定的。本方法中依靠飞行方向的转折点及航向改变点即为一个中间节点。改变航向即是无法进行两点之间直线飞行时，遇到障碍物时会发生方向的改变。将每一个方向的改变点作为一个中间节点，以此为基础构成图。如何选择中间节点是此方法的一个关键步骤，建立了足够的中点节点构建图，才能进行最短路径计算，初始节点是图的根，而中间节点就是图的叶，必不可少。

第一步确定坐标，首先建立地球中心坐标系，采用地图工具标注出初始点的坐标为S(x,y),目标节点为G(x,y),并标注出障碍物(利用检测仪检测到的异于无人机的阻碍无人机从始节点到终端节点的一个物体)坐标Z(x,y),建立起三个节点的坐标，为图的组成提供基础节点，路径动态规划的前提。所述结构体包括LinkNode和Node，其中结构体变量包括：邻接的结点在数组中的编号vex，指向下一个节点next，节点所存数据data，列表头节点head，并以此来建立图，具体设计如下：

第二步选择中间节点，首先初始化根节点S(x,y)航向角θ₀，比较点i处的航向角θ_i与前一航向角θ_i-1，判断是否相等，若相等，则i点不能选择为中间节点，若不相等则i就是其中一个中间节点。

一个节点为N[i-1],从此节点开始向目标节点开始运动。当遇到障碍区改变航向时，确定中间节点为N[i]。而方向是否改变采用检测仪可探测到与水平方向的夹角是否变化。如图4，中间节点距离障碍物的距离如何确定，确定点N(i)。建立直角坐标系，N(i-1)点通过x轴对称成为N’(i-1)，连接N’(i-1)与N(i+1)与纵坐标交点即为N(i)点。

第三步是最佳路径选择，本方法中采用floyd算法，从始节点到中间节点的选择到目标节点，将始节点作为根节点，从跟节点到目标节点进行遍历，组建成一个图，相关矩阵变化如下：

采用floyd方法进行最佳路径规划，包含变量节点个数vertexnum，权重weight，将每次算法计算得到的路径都存放path[]中，算法实现如下：

通过以上的权重矩阵和路径矩阵的矩阵运算可以算出最佳路线，得最佳规划路线如图4所示，从根节点到目标节点的最短路径。

以上实施例仅用以说明本发明的技术方案而非限制，尽管参照较佳实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，可以对本发明的技术方案进行修改或者等同替换，而不脱离本发明技术方案的宗旨和范围，其均应涵盖在本发明的权利要求范围当中。