基于最大相关熵的地震子波信号提取方法与流程

本发明属于地震资料处理技术领域，具体涉及一种基于最大相关熵的地震子波信号提取方法的设计。

背景技术：

地震子波是进行地震资料高分辨率处理、正演模拟和储层参数反演的基础。子波不准确，会导致反演所获得的阻抗不可靠，进而导致地震数据高分辨率处理得不到理想的高保真剖面。因此，地震子波的精确估计一直是勘探地球物理领域关注的核心问题之一。地震子波提取的基本框架是褶积模型，包括子波、反射系数序列、含噪声地震道。对于地震子波估计目前常用方法可以分为两类：一类是统计性提取方法，一类是确定性提取方法。

确定性子波提取方法需要有测井资料和地震资料共同参与，首先通过测井数据算出反射系数序列，然后通过井旁道反演得到地震子波。确定性子波提取方法能得到较为准确的子波，但很容易受各种测井误差的影响，尤其是声波测井资料不准而引起的速度误差会导致子波振幅畸变和相位谱扭曲。目前主要方法有维纳滤波法、线性反演方法、贝叶斯方法等。

另一种提取方法叫做统计性子波提取方法，该方法不需要测井信息，类似于信号处理中的盲系统辨识问题。如果将地层反射系数看作输入，将子波看作系统函数，则统计性子波提取就是在地层反射系数和子波都未知的情形下，根据观测到的地震数据估计地震子波的问题。该类方法不需要测井数据参与，但是需要对地震资料和地下反射系数序列的分布进行某种假设，所得到子波精度与假设条件的满足程度有关。目前主要方法有自相关法、高阶统计量方法、复赛谱估计方法等。在勘探工区有测井数据时，刘洁等在对比了确定性最小平方法，统计性复赛谱和双谱法优缺点后表明在实际数据中采用确定性的子波提取方法要明显优于统计性方法。

确定性子波估计方法的基本原理基于褶积模型：

s＝w(t)*r(t)+n(t)

如果从测井数据提取反射系数r(t)，则可以根据观测的地震数据采用最小二乘的方式构建目标函数极小进行求解：

对上式求偏导，可以构建如下方程：

其中φ_rr表示反射系数自相关函数，ψ_xr表示地震记录与反射相似的互相关函数，直接求解方程式就能得到需要估计的地震子波。但是在求解结果过程中由于算法影响会导致子波旁瓣效应明显，为此张广智等采用多道相关计算得到初始子波，通过迭代反演方法精细求解井旁道地震子波。但是实际观测的地震数据存在噪声，而且反射系数还存在标定不准和计算误差等因素，这些都会导致子波计算存在误差，尤其是非高斯噪声存在时，如何得到高精度的地震子波估计结果需要深入研究。

相关熵的概念最早在2006年被Santamaria等人提出，其想法最初是为解决信息理论学习中不能在同一测量函数中处理随机序列时间结构及其统计分布的问题，提出的一种广义相关函数，进一步地，Liu等又将该广义相关函数推广到两个随机变量的情形，从而形成了相关熵的概念，相关熵作为一个非线性鲁棒算法，已被成功应用于信号处理和机器学习等多个领域，比如鲁棒回归分析、滤波、降维、分类和人脸识别等。近年来研究表明最大相关熵准则可以有效压制非高斯噪声，下面简要介绍最大相关熵的基本原理。

设两随机变量为X,Y，它们的相关熵定义为：

V_σ(X,Y)＝E[k_σ(X-Y)]＝∫K(x,y)dF_XY(x,y)

其中E表示期望算子，k_σ(·)表示满足Mercer条件的正定核函数，F_XY(x,y)表示两个随机变量的联合分布函数。实际问题中该联合概率密度函数往往是未知的，此时可以利用有限样本数据对来获得相关熵的一个估计式：

一般情况下上式中的核函数采用高斯核，则上式可写成：

其中σ＞0为核宽。当X,Y间的相似度越高时，上式的值就越大，最大化上式即为最大相关熵准则(Maximum Correntropy Criterion,MCC)。

相比于其他相似性度量准则，比如最小二乘准则，相关熵准则有如下优点：

(1)该准则包含所有偶数阶矩并可用于非线性和非高斯信号处理；

(2)核函数能够有效控制高阶矩加权；

(3)该准则实际是一个局部相似性度量准则，因此该准则对离群点具有较好的鲁棒性。

技术实现要素：

本发明的目的是为了解决现有技术中基于最小二乘法的确定性子波估计方法在实际测量过程中由于地震数据存在噪声，而且反射系数还存在标定不准和计算误差等因素，导致子波计算存在误差，精度较低的问题，提出了一种基于最大相关熵的地震子波信号提取方法。

本发明的技术方案为：基于最大相关熵的地震子波信号提取方法，包括以下步骤：

S1、利用高斯核作为核函数，构建离散的相关熵表达式；

S2、将地震反演模型、现有观测数据以及反射系数代入相关熵表达式，得到目标函数；

S3、将目标函数转换为取极小值形式；

S4、采用拟共轭梯度反演算法求解目标函数，得到需要估计的地震子波。

进一步地，步骤S1中构建的离散的相关熵表达式为：

式中σ为核宽且σ＞0，N表示数据X和Y的长度，x_i和y_i分别表示数据X和Y的第i项。

进一步地，步骤S2具体为：

将地震反演模型s＝w(t)*r(t)+n(t)、现有观测数据x(t)_obs以及反射系数r(t)代入相关熵表达式，其中，观测数据x(t)_obs即地震反演模型中的s，w(t)为本发明要计算求解的地震子波，r(t)为表征地层特性的向量，即反射系数，n(t)为表征地震反演模型中存在的加性噪声；

得到目标函数：

进一步地，步骤S3中将目标函数转换为取极小值形式后表示为：

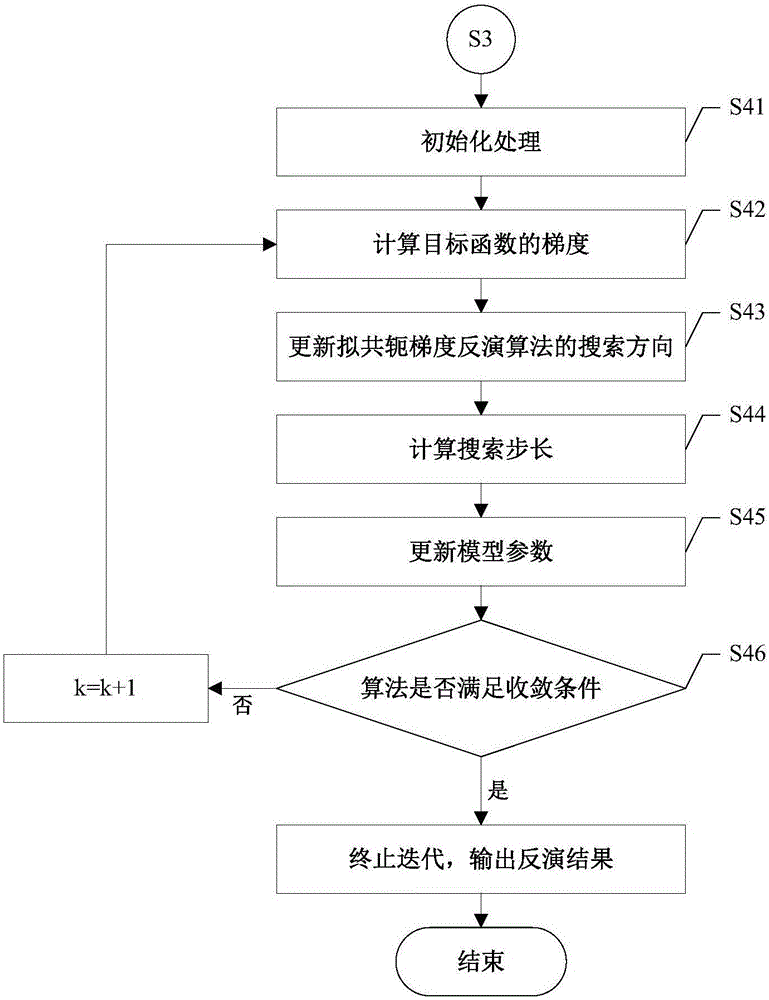
进一步地，步骤S4具体包括以下分步骤：

S41、初始化处理，设置初始模型x₀＝w，w为需要估计的地震子波且以零向量作为初始值，置迭代次数k＝0；

S42、计算目标函数obj的梯度g_k；

S43、更新拟共轭梯度反演算法的搜索方向：若k＝0，则p_k＝-g_k，否则有：

式中p_k表示搜索方向，y_k-1表示梯度增量，z_k-1表示共轭方向，β_k为搜索方向的遗忘因子，b_k为搜索方向更新公式中的梯度增量系数；

S44、计算搜索步长α_k：

式中G为反射系数自相关函数构造的矩阵，e_k表示第k次迭代估计残差；

S45、更新模型参数：

x_k+1＝x_k+α_kp_k (6)

S46、检查算法是否满足收敛条件，若是则终止迭代，输出反演结果x^*＝x_k+1作为需要估计的地震子波w，否则令k＝k+1，返回步骤S42进行迭代。

本发明的有益效果是：本发明将勘探地球物理学中的地震子波估计方法与信息理论学习中最大相关熵准则进行结合，提出了基于最大相关熵的地震子波估计方法，采用最大相关熵准则替换原有最小二乘准则，使得目标函数能够更好的克服非高斯噪声。模型和实际资料均表明，本发明相对于传统最小二乘方法鲁棒性更强，精度更高，更有利于进行地质勘探中的资料处理。

附图说明

图1为本发明提供的基于最大相关熵的地震子波信号提取方法流程图。

图2为本发明步骤S4的分步骤流程图。

图3为本发明实施例的混合相位地震子波模型和模型反射系数示意图。

图4为本发明实施例的无噪声合成地震记录和不同方法反演结果对比示意图。

图5为本发明实施例的含6db高斯噪声合成地震记录和不同方法反演结果对比示意图。

图6为本发明实施例的含6db拉普拉斯噪声合成地震记录和不同方法反演结果对比示意图。

图7为本发明实施例的实际工区估计子波结果对比示意图。

图8为本发明实施例的实际工区估计子波合成记录与真实地震记录结果对比示意图。

具体实施方式

下面结合附图对本发明的实施例作进一步的说明。

本发明提供了一种基于最大相关熵的地震子波信号提取方法，如图1所示，包括以下步骤：

S1、利用高斯核作为核函数，构建离散的相关熵表达式：

式中σ为核宽且σ＞0，N表示数据X的长度(数据Y长度等同X)，x_i和y_i分别表示数据X和Y的第i项。

S2、将地震反演模型s＝w(t)*r(t)+n(t)、现有观测数据x(t)_obs以及反射系数r(t)代入相关熵表达式。其中，观测数据x(t)_obs即地震反演模型中的s，w(t)为本发明要计算求解的地震子波，r(t)为表征地层特性的向量，即反射系数，n(t)为表征地震反演模型中存在的加性噪声，本发明实施例中为6dB高斯噪声或者6dB拉普拉斯噪声。

得到目标函数：

S3、将目标函数转换为取极小值形式：

S4、采用拟共轭梯度反演算法求解目标函数，得到需要估计的地震子波。

该步骤中，用拟共轭梯度反演算法的原因在于，从公式(3)结构来看，该公式是高度非线性的，如果直接求导很难得到解析解，因此我们采用迭代求解方式对该目标函数进行求解。

在处理病态优化问题时，共轭梯度算法和拟牛顿迭代算法都是常用的算法。通常情况下，前者的收敛速度较后者低，但后者在计算海森矩阵逆时需要花费较大存储空间。因此，本发明基于求解算法稳定性、低存储性和迭代速率等综合考虑，采用Zhang et.al(2013)提出的拟共轭梯度反演算法(它结合了共轭梯度算法和拟牛顿迭代算法)进行求解运算。此外，由于原始算法中需要根据不同的广义极值分布目标函数来计算步长不具有普适性，我们直接采用Dianne(1991)提供的步长搜索的代码修改该步骤，由于该搜索方法只需要给出计算目标函数的值和梯度的两个函数便能够搜索得到步长，因此可以使得上述算法能适应任意目标函数情形。

如图2所示，该步骤包括以下分步骤：

S41、初始化处理，设置初始模型x₀＝w，w为需要估计的地震子波且以零向量作为初始值，置迭代次数k＝0。

S42、计算目标函数obj的梯度g_k。

S43、更新拟共轭梯度反演算法的搜索方向：若k＝0，则p_k＝-g_k，否则有：

式中p_k表示搜索方向，y_k-1表示梯度增量，z_k-1表示共轭方向，β_k为搜索方向的遗忘因子(Polak–Ribiere–Polyak(PRP)conjugate gradient method搜索算法的系数)，b_k为搜索方向更新公式中的梯度增量系数。

S44、计算搜索步长α_k：

式中G为反射系数自相关函数构造的矩阵，e_k表示第k次迭代估计残差。e_k＝x_k*r(t)-d，x_k为第k次迭代估计出的子波，r(t)为反射系数，d为观测数据，即x(t)_obs。

S45、更新模型参数：

x_k+1＝x_k+α_kp_k (6)

S46、检查算法是否满足收敛条件，本发明实施例中，收敛条件为||g_k||≤ε，ε为一个极小的正数。若是则终止迭代，输出反演结果x^*＝x_k+1作为需要估计的地震子波w，否则令k＝k+1，返回步骤S42进行迭代。

下面以两个具体实施例对本发明的提取效果做具体说明：

实施例一：

本发明实施例中我们采用的是人为构造的地震子波，并用最大相关熵进行提取该子波。

实际地震记录中，地震子波往往是混合相位的，因此我们直接以混合相位子波(图3)为模型计算合成地震记录，已知反射系数如图4所示，将反射系数与地震子波褶积形成地震记录如图5所示，下面我们根据最大相关熵准则测试提取子波结果，为了验证算法的鲁棒性，同时对比了在最小二乘条件下估计子波结果。图4为无噪声环境下合成地震记录及提取子波结果，可以发现在无噪声环境下，两种方式都能得到较好的估计效果。

为分析最大相关熵准则对含噪声记录的鲁棒性，我们首先分析了在含有6db高斯噪声情形下(图5a)子波反演结果(图5b)。同理，当合成地震信号含有6db拉普拉斯噪声(非高斯噪声)时(图6a)，反演结果如图6b所示。从含噪声结果来看，在有噪声条件下，最小二乘准则所估计的子波振荡性较强，最大相关熵估计结果与原始子波匹配较好，尤其是对非高斯噪声，最小二乘准则所得到结果误差较为明显，而最大相关熵能够较好地恢复地震子波真实形态，由此可见最大相关熵准则条件下地震子波估计方法比最小二乘准则具有更强的鲁棒性。

实施例二：

本发明实施例中，我们采用我国西部某油田实际工区进行了地震子波估计。首先提取过井地震记录，并对井曲线做分块处理得到反射系数序列，然后通过最大相关熵准则和最小二乘准则对地震子波进行估计，得到结果如图7所示。为了验证结果有效性，我们通过合成记录与井旁合成记录对比来进行验证。图8是最大相关熵准则提取子波合成地震记录、最小二乘准则提取子波合成记录与井旁地震道对比，可以发现最大相关熵准则提取子波合成记录与井旁道差异较小，整体均方误差为2.3，而最小二乘准则下得到地震子波合成记录整体均方误差为3.6，由此可见，基于最大相关熵准则的地震子波提取方法比传统的最小二乘准则下子波提取方法精度更高，鲁棒性更强。

本领域的普通技术人员将会意识到，这里所述的实施例是为了帮助读者理解本发明的原理，应被理解为本发明的保护范围并不局限于这样的特别陈述和实施例。本领域的普通技术人员可以根据本发明公开的这些技术启示做出各种不脱离本发明实质的其它各种具体变形和组合，这些变形和组合仍然在本发明的保护范围内。