一种基于简化远距离电磁场计算的方法与流程

本发明涉及雷电定位与电磁场计算领域，具体的指一种使用Matlab语言计算衰减因子，与理想场进行卷积求得衰减电磁场的方法。

背景技术：

雷电产生的甚低频(VLF,3-30kHz)和低频(LF,30-300kHz)信号可以传播很远，在数百公里到上千公里处都可以观测到。地波沿着地球表面进行传播，在传播过程中主要受地表电导率的影响，发生衰减与色散。同时由于传播距离远，要考虑地球曲率造成的影响，会使观测结果相较于沿平直方向传播不同。这些影响因子会干扰观测者根据观测数据判断闪电类型、反演电流矩、进行地基闪电定位等。

雷电产生的电磁场在传播过程中包含水平电场、垂直电场和水平磁场三部分。Delfino^[1],[2]研究了Cooray-Rubinstein(C-R)算法的有效性，此算法用来计算雷电产生的水平电场，Delfino指出C-R算法有一个理想的计算精度。水平电场包含大量高频成分，在传播距离很远时几乎全部衰减掉，远距离观测主要采集垂直电场信号和水平磁场信号。对于垂直电场的研究，Cooray^[3],[4]等利用Sommerfeld积分的精确解验证了近似算法的准确度。Shooray^[5]等利用时域有限差分法(FDTD)研究了Wait算法的准确性，并指出在距离闪电通道10-100km范围内，Wait算法计算出的垂直电场峰值与波形与FDTD的计算结果有很好的对应。在信号传播距离达到数千公里时，长波长的VLF波导传播模型已被成功开发应用，此模型更适用于窄频段的信标信号。对于自然闪电产生的宽带信号而言，这种模型滤掉了过多波形特征，导致结果与回击产生的信号不同，使接收到的信号更像一个脉冲信号而不是闪电信号。Cummer^[6]和Hu^[7]提出了一种改进的二维柱坐标FDTD模型，此模型可用来计算地面-电离层电磁场传播，截止频率为30kHz。这种算法的结果与Pappert和Feguson^[8]的波导模型有很好的一致性，与ELF-VLF的闪电观测结果相对应。但相较于Wait算法，此模型计算时间较长，且对计算频率有限制，计算过程中存在色散问题。

本发明主要关注闪电产生的电磁场信号传播至远距离处(数百至上千公里)的特征，这些信号对于全球闪电定位、电流矩与电荷矩的反演起到至关重要的作用。尽管Wait算法^{[9],[10],[11]}已经指出远距离电磁场传播的计算方法，但此算法在计算过程中过于复杂，本发明试图利用一种近似算法对远距离电磁场传播进行计算，以简化计算过程。

本发明的技术解决方案步骤如下：

步骤1，计算理想条件(地球曲率半径无穷大，电导率无穷大)下传播一定距离(数百千米)的电场E₀和磁场B₀，进行傅立叶变换得到频域场E_w和B_w；

E_w＝fft(E₀)，B_w＝fft (1)

步骤2，根据W.Sollfery^[12]提出的近似算法，计算曲率衰减因子W₁：

ts可表示为：

t_s＝e^-iπ/3τ_s＝e^-iπ/3(3πv_s/2)^2/3

步骤3，根据Wait算法，计算电导率衰减因子W₂：

Δ为土壤等效表面阻抗，表达式为

步骤4，将计算得到的衰减因子W₁、W₂分别与理想频域场E_w、B_w进行卷积得到频域衰减场E_G、B_G，进行傅立叶逆变换即得到时域的衰减电场E_t与磁场B_t。

E_G＝E_w×W₁×W₂，B_G＝B_w×W₁×W₂ (7)

E_t＝ifft(E_G)，B_t＝ifft(B_G) (8)

本发明的优点是：

1.相比于传统Wait算法，本发明提出的近似算法简化了计算过程，同时又可以保证计算结果在一定范围内的准确性，为远距离电磁场传播的衰减提供了新的计算思路。

相比于时域有限差分法(FDTD)，利用本算法可以节省计算时间，同时两种方法得到的结果相近，优化了传统Wait算法。

附图说明

图1本发明的基于简化远距离电磁场计算的方法总体流程图；

图2-1为300km处理想电场波形图；

图2-2为300km处理想磁场波形图；

图3-1为300km处衰减电场波形图；

图3-2为300km处衰减磁场波形图。

具体实施方式

本发明为基于简化远距离电磁场计算的方法。其特征是：首先计算出理想条件(地球曲率半径无穷大，电导率无穷大)下传播一定距离的电场和磁场，并进行傅立叶变换得到频域场；分别计算电导率衰减因子W₁与地球曲率半径衰减因子W₂，将两因子与理想场进行卷积，得到频域衰减的电场和磁场；进行傅立叶逆变换即得到时域衰减电场和磁场。由于Cummer提出的时域有限差分法(FDTD)已在其论文中有了充分论述证明，本专利利用这种方法对计算结果进行对比修正，使结果更加准确可信，从而达到简化Wait算法，更加便捷计算远距离电磁场传播的目的。流程图如图1所示。

(1)首先计算理想电场与磁场，闪电源采用电流矩源，这种电流矩便于加入到FDTD模型中进行计算，表达式为

式中I₀＝20kA，ν₀＝8×10⁷m/s，γ＝3×10⁴/s，a＝2×10⁴/s,b＝2×10⁵/s。

利用此电流矩源计算出传播至一定距离处的理想电场与理想磁场，进行傅立叶变换得到频域的理想场E₀和B₀：

E_w＝fft(E₀)，B_w＝fft(B₀) (2)

(2)根据W.Sollfery提出的近似算法，计算曲率衰减因子W₁：

式中x＝(k₀R_e/2)^1/3φ，k₀为波数，表示为φ代表闪电源与接收端间的弧度，R_e表示地球半径，闪电源与接收端的球面距离可以表示为ρ＝R_e×φr。

t_s可表示为：

t_s＝e^-iπ/3τ_s＝e^-iπ/3(3πv_s/2)^2/3

s的取值为0,1,2,3...其中s＝0时误差为0，s＝1时误差为0.0024，s＝2时误差小于0.0012，s取值越大，误差越小，在大于2时误差均小于0.0005。把方程(4)中求出的t_s代入方程(3)，求出的W即为地球曲率衰减因子W₁。

(3)根据Wait算法，计算电导率衰减因子W₂：

式中“erfc”表示误差方程，d是闪电通道与观测点之间距离，ω表示角频率，c表示光速，Δ为土壤等效表面阻抗，表达式为

ω是信号角频率，ε_r为地面相对介电常数，ε₀为真空介电常数，μ₀为真空磁导率，σ为地表电导率。

(4)将计算得到的衰减因子W₁、W₂与理想频域场E_W和B_W进行卷积得到衰减频域场E_G和B_G，卷积过程如下：

E_G＝E_w×W₁×W₂，B_G＝B_w×W₁ (8)

(5)对频域衰减场E_G和B_G进行傅立叶逆变换，即可得到时域远距离衰减场E_t与B_t。傅立叶逆变换过程如下：

E_t＝ifft(E_G)，B_t＝ifft (9)

具体实例

见图1 300km处理想电场与磁场波形图：

两种方法得到的理想场峰值有差距，可用FDTD结果对本发明的算法进行修正，使两种方法计算出的理想电场相近，以便后面衰减结果分析。

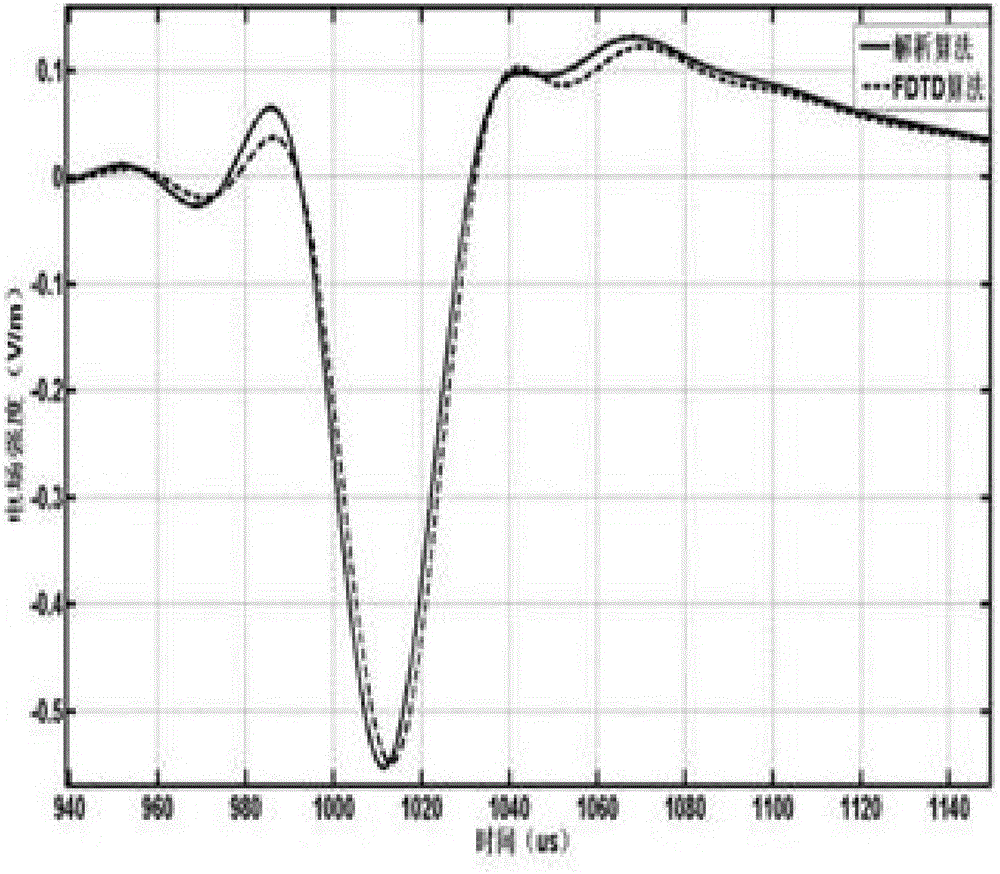
在采用相同理想场后，接下来我们要对两种算法计算得到的衰减电场和衰减磁场进行对比分析。图2是300km处衰减电场与磁场波形图；

对比可以看出，两种方法得到的结果非常相近，说明采用本专利提出的新算法可以准确计算远距离电磁场的衰减。