一种固体氧化物燃料电池电堆内部温度分布的预测方法与流程

本发明属于燃料电池领域，更具体地，涉及一种固体氧化物燃料电池电堆内部温度分布的预测方法。

背景技术：

固体氧化物燃料电池(Solid Oxide Fuel Cell,简称SOFC)发电技术以其高效、环保、安静的优点而成为21世纪最具应用前景的供电技术之一。尽管SOFC相关技术在近年得到了快速发展，但为了尽快实现其商品化仍有许多问题需要解决，而SOFC电堆内温度和温度梯度的监测即是其中最突出的障碍之一。

电堆运行过程中，气体流向上的反应物的浓度会随着阳极—电解质—阴极(Positive electrode-Electrolyte-Negative electrode，简称PEN)层电化学反应的进行而逐渐不均匀，使得相应的电流密度也分布不均匀，而不均匀的反应物浓度和电流密度等综合因素会导致电堆在气体流向上产生空间温度梯度。大的空间温度梯度会在电池上产生较大的热应力，而电池的PEN三层结构决定了其能承受的热应力有限，过大的热应力会导致电池片变形甚至破裂，从而缩短电池使用寿命，另一方面，SOFC电堆内部的最大工作温度过高会损害材料的耐久度和电池性能，因此，为了SOFC能够稳定、长寿命的运行，必须把电堆的最大温度及最大温度梯度控制在材料能承受的范围之内；然而，从实物开发角度来说，SOFC电堆内部的电池片上并不能安装太多热电偶之类的温度检测装置，否则电堆的良好气密性及高发电性能将会受到严重影响，所以电堆温度控制系统中需要用到的电堆温度分布情况无法直接通过传感器测量直接得到。因此设计出电堆温度观测器，通过有限的可测量的电堆参数，快速准确地预测出电堆内部的温度分布情况是电堆工作温度控制工作中非常关键的一步。

技术实现要素：

针对现有技术的以上缺陷或改进需求，本发明提供了一种固体氧化物燃料电池电堆内部温度分布的预测方法，通过对电堆进行动态建模并线性化，并将其应用到卡尔曼滤波温度观测器中，由此解决燃料电池电堆内部温度分布的预测的技术问题。

为实现上述目的，按照本发明的一个方面，提供了一种固体氧化物燃料电池电堆内部温度分布的预测方法，其特征在于，该预测方法包括下列步骤：

(a)将固体氧化物燃料电池SOFC电堆进行有限元处理，即将该电堆划分为若干个串联的相同动态特性的单电池片，且每个所述单电池片沿着气体流向分为多个节点，利用物理守恒定律对所述电堆进行动态建模得到所述节点的多个非线性模型；

(b)将所述非线性模型线性化处理后得到线性化模型，将所述电堆的总电流，入口氢气流量和入口空气流量作为输入，对比每个所述节点输出的空气层温度和固体层温度经过所述非线性化模型与线性化模型在阶跃扰动下的动态响应结果，二者结果相同，由此验证所述线性化处理的合理性；

(c)将所述线性化模型离散化得到所述电堆在不同时刻的状态估计变量和测量信号，将该状态估计变量和测量信号应用到卡尔曼滤波观测器中计算出所述观测器中的参数矩阵，预设所述单电池片中的每个所述节点的固体层和空气层的温度作为状态初值，通过递推迭代计算到每个时刻所述电堆内部的温度，由此实现所述电堆内部温度的预测。

作为进一步优选地，步骤(a)中，在所述有限元处理中所述电堆满足下列特性：

(I)所述气体为理想气体，

(II)所述电堆与外界是隔热，

(III)每个所述节点的电势相等，

(IV)所述气体的流出节点的温度和摩尔分数等同于该节点内相应的温度和摩尔分数，

(V)沿所述气体的气流方向，上一个所述节点的输出等于下一个所述节点的输入。

作为进一步优选地，步骤(a)中，所述多个节点优选采用5个节点。

作为进一步优选地，步骤(a)中，所述动态建模的模型优选采用二阶温度模型，其中，该模型中包括每个所述节点的氢气摩尔分数子模型、空气摩尔分数子模型、空气层温度子模型、固体层温度子模型和电化学子模型。

作为进一步优选地，步骤(b)中，所述线性化处理优选采用泰勒级数展开的方法，保留展开后的线性化部分，舍弃高阶项。

作为进一步优选地，步骤(b)中，所述阶跃扰动优选采用电堆电流5A、电堆阳极入口气体流量20％、电堆阴极入口气体流量20％的阶跃扰动。

作为进一步优选地，步骤(c)中，所述卡尔曼滤波观测器优选采用下列表达式，其中，是所述电堆k时刻的内部温度状态估计值，是第k-1时刻到第k时刻的最优预测项，是修正项，K_k是第k时刻的滤波增益，Z_k是k时刻所述电堆的测量信号，H是所述电堆的测量矩阵，

总体而言，通过本发明所构思的以上技术方案与现有技术相比，能够取得下列有益效果：

1、本发明通过对SOFC电堆内部温度分布建立了一个描述气流方向上物理变量分布状况的物理模型，能够反映实际电堆内部物理变量的变化情况，同时将每层单电池片沿着气体流向分为5个节点，不仅能够反映出电池片内部各节点的温度，也能够反映出气流方向上的温度梯度的变化情况，为后续温度观测值与模型的模拟值对比提供基础；

2、本发明通过建立氢气摩尔分数子模型、空气摩尔分数子模型、空气层温度子模型、固体层温度子模型和电化学子模型，表述了一个节点内的气体摩尔分数、气体层与固体层温度、电压、电流等主要变量的耦合关系，反映出一个节点的各变量的动态变化情况，进而能够反映出单电池片以及电堆的动态变化情况；

3、本发明通过采用泰勒级数展开的方法将非线性模型线性化处理，并通过仿真验证了线性化模型可以准确反应电堆动态响应，便于将线性化模型参数运用到线性卡尔曼滤波理论中，实现温度状态的预测；

4、本发明通过采用线性卡尔曼滤波温度观测器，能够准确地预测在线性化操作点处的电堆电池片温度分布情况，并且抗扰动性良好，使得在电堆初始温度值出现误差时仍能快速跟踪上电堆内部温度分布。

附图说明

图1是按照本发明的优选实施例所构建的SOFC电堆内部温度分布预测方法的流程图；

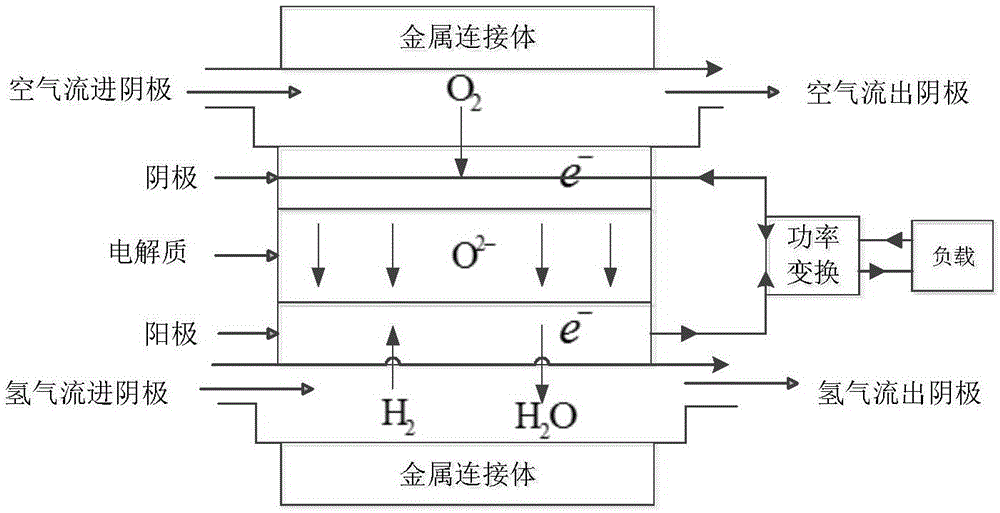
图2是按照本发明的优选实施例所构建的SOFC单电池结构及其工作原理示意图；

图3是按照本发明的优选实施例所构建的SOFC电堆有限元分割示意图；

图4是按照本发明的优选实施例所构建的卡尔曼滤波算法原理图；

图5是按照本发明的优选实施例所构建的用观测器来估计SOFC电堆温度分布的示意图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。此外，下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。

本发明针对SOFC电堆内部温度分布因操作难度大而难以测量实现的问题，提供了一种SOFC电堆内部温度分布的预测方法。该方法仅需要获得系统输入：电堆总电流、入口氢气和空气的摩尔流量，以及出口的固体层和空气层温度，即可以估计出电堆内的温度分布，从而为电堆温度控制提供基础，确保电堆安全长寿命的运行。

按照本发明的一个方面，图1是按照本发明的优选实施例所构建的SOFC电堆内部温度分布预测方法的流程图，如图1所示，采取了如下技术解决方案：

一、电堆建模

SOFC电堆由若干片单电池串联而成，假设每片单电池具有完全相同的动态特性。因此只需对单电池进行建模，然后简单组合形成电堆模型即可。将单电池分别沿着气体流向从气体入口到出口依此等分为5个节点，并对每个节点做出如下假设：

(1)所有气体均为理想气体；

(2)电堆与外界是隔热的；

(3)由于连接体金属的高导电性，各节点电势相等；

(4)气体流出节点的温度和摩尔分数等同于该点内相应的温度和摩尔分数；

(5)沿气流方向上，上一个节点的输出等于下一个节点的输入；

基于以上假设，对SOFC单电池建模如下：

单电池片第m个节点的氢气摩尔分数子模型：(该模型表述了由上一个节点的氢气摩尔分数和摩尔气体流量计算得到当前节点的氢气摩尔分数和摩尔气体流量)

单电池片第m个节点的空气摩尔分数子模型：(该模型表述了由上一个节点的氧气摩尔分数和摩尔气体流量计算得到当前节点的氢气摩尔分数和摩尔气体流量)

其中，和分别为第m个节点内的氢气、水、氧气和氮气的摩尔分数，和分别为第m个节点内阳极和阴极的气体摩尔总数，和分别为第m个节点的阳极和阴极气体的摩尔气体流量，i^m是第m个节点内的电流，F为法拉第常数。

单电池片第m个节点内的空气层温度子模型：(该模型表述了由上一个节点的气体摩尔分数、摩尔气体流量以及前一结点的空气层的温度计算得到当前节点的空气层温度)

其中，和分别为氮气的比热和热焓，R为理想气体常数，和分别为氧气的比热和热焓，C_k(k＝1,2,3,4,5)是取值为常量的系数。

对于固体层温度建模，因边缘节点的特殊性，即第一个节点无前节点，最后一个节点无后节点，节点(1,5)建模原理与节点(2,3,4)建模原理存在差异。因此建模时分别处理节点1,节点5与节点(2,3,4)，如下：

单电池片边缘节点(即m＝1,5时)的固体层温度子模型分别为：(模型可得到该节点的固体层温度)

单电池片中间节点(即m＝2,3,4时)固体层温度子模型为：

其中，V_cell是电堆内单电池的工作电压，和分别为氢气和水蒸气的热焓，ρ_ic、c_ic和τ_ic分别表示固体层的密度、比热和厚度；ρ_pen、c_pen和τ_pen则分别表示电池片PEN结构的密度、比热和厚度。

单电池第m个节点内的电化学子模型为：(该模型表述了V_cell和i^m之间的关系，可通过模型的得到电堆总电压或总电流)

其中，V_cell是电堆内单电池的工作电压；是第m个节点内的等效电阻，也是是电池片极化损失电压、欧姆损失电压和浓差损失电压的电阻等效值，本例中由实际试验数据辨识得出；是第m个节点的能斯特电压。

SOFC电堆由若干片单电池串联而成，将单电池分别沿着气体流向从气体入口到出口依此等分为5个节点，每个节点包含五个子模型，子模型之间通过变量的耦合连接，构成一个节点的模型。由单个节点扩充到电电池片，再扩充到电堆模型。

图2按照本发明的优选实施例所构建的SOFC单电池结构及其工作原理示意图，如图2所示，阳极的氢气气体和阴极的空气都从电池的同一侧进入电池内部后，在催化剂层发生电化学反应，产生的电流经过功率变化装置用于供给外部负载，电池内产生的废气及未反应完的气体从电池的另外一侧输出；图3是按照本发明的优选实施例所构建的SOFC电堆有限元分割示意图，如图3所示，将单电池分别沿着气体流向，从气体入口到出口依此等分为M个节点，每个节点有如下相同假设：节点内所有气体均为理想气体，由于连接体金属的高导电性，各节点电势相等；气体流出节点的温度和摩尔分数等同于该点内相应的温度和摩尔分数；沿气流方向上，上一个节点的输出等于下一个节点的输入。

二、模型线性化及合理性验证

SOFC电堆模型方程均为一阶微分方程，可采用二元函数简记为如下形式：

给SOFC电堆模型一个适当的输入，等模型运行稳定时，记录下模型所涉及变量的稳态值为(x₀,y₀)。这意味着变量x在数值下(x₀,y₀)不再变化，因此有采用泰勒级数展开公式将电堆在常用稳态操作点处线性化，可得到方程右端函数展开如下：

f(x,y)＝f(x₀,y₀)+f_x(x₀,y₀)(x-x₀)+f_y(x₀,y₀)(y-y₀)

+o(x-x₀)+o(y-y₀)

其中，f_x(x₀,y₀)、f_y(x₀,y₀)分别表示函数f(x,y)对变量x和y的一阶偏导在(x₀,y₀)处的值；o(x-x₀)、o(y-y₀)则分别表示x-x₀和y-y₀的高阶无穷小。

略去二阶及以上无穷小项后为原函数的线性化函数：

f(x,y)≈f(x₀,y₀)+f_x(x₀,y₀)(x-x₀)+f_y(x₀,y₀)(y-y₀)

实际模型方程会涉及到多元函数，线性化处理方法相同。

对每个节点的固体层和空气层温度的线性化之后的结果可以表示如下：

为整个电堆状态变量，包括每个节点固体层和空气层的温度，为模型的输入，即整个电堆的电流、阳极摩尔流量，阴极摩尔流量，为模型的输出，即整个电堆出口的空气层和固体层温度，A为电堆10*10维的系统矩阵，B为系统10*3维的输入矩阵，C为系统2*10维的输出矩阵。

线性化处理仅保留了原函数的局部性质，所以要对线性化的模型进行检验，以验证其对原模型的可替代程度。检验方法是，对原非线性模型与线性化处理的模型，给定相同的输入条件，运行稳定后，在不同的时刻分别给三个输入量(即电堆总电流I_tot，电堆入口氢气流量和电堆入口空气流量)以5A、20％、20％的阶跃扰动，分别对比线性模型与与非线性模型中节点的空气层温度和固体层温度的响应，二者均表现出了一致的动态响应且任意节点内的温度误差均不超过5℃。该误差很小，在可接受的范围之内。因此，可以用线性化模型来代替原电堆模型，进行温度观测器的设计。

三、观测器设计

将SOFC电堆线性化之后的模型，表达成以下形式：

将以上系统模型离散化,便于观测器设计及计算机仿真的结构，如下：

其中，X_k表示k时刻电堆的状态估计变量(对应Φ是电堆的一步状态转移矩阵(对应线性化模型中的A矩阵)，G是电堆的输入控制矩阵(对应线性化模型中的B矩阵)，U_k-1是电堆k-1时刻的控制量(对应)，Γ是电堆噪声驱动矩阵，W_k-1是k-1时刻的电堆过程噪声序列；Z_k-1是k-1时刻的电堆测量信号(对应)，H是电堆量测矩阵(对应线性化模型中的C矩阵)，V_k-1是k-1时刻的量测噪声。

基于卡尔曼滤波的观测器设计为如下：

是加入观测器之后系统k时刻的状态估计值，分为两项，其中作为由第k-1时刻到第k时刻的最优预测项，作为状态的修正项，K_k是第k时刻的滤波增益。

具体如下：

获取电堆温度状态变量的最优预测值：

获取一步预测误差协方差：P_k/k-1＝ΦP_k-1Φ^T+ΓQΓ^T

获取滤波增益：K_k＝P_k/k-1H^T(HP_k/k-1H^T+D)^-1

获取估计误差协方差：P_k＝(I-K_kH)P_k/k-1

获取电堆温度状态变量的最优估计值：

其中，P_k/k-1是第k-1时刻到第k时刻的预测误差协方差阵，P_k是第k时刻更新的误差协方差阵，Q是电堆过程噪声序列的协方差阵，D是量测噪声的协方差阵，I表示单位矩阵。

当给定电堆温度状态初值X₀和一步预测误差协方差阵初值P₀后，先预测求出最优预测项再由得到修正项，它们叠加即是当前时刻的状态估计值。滤波算法通过不停的递推迭代计算，不断更新状态变量，根据递推计算出电堆在k时刻的内部温度状态估计即可估计出电堆内整个温度的分布情况。

图4是按照本发明的优选实施例所构建的卡尔曼滤波算法原理图，如图4所示，卡尔曼滤波算法中，给定系统状态初值X₀和一步预测误差协方差阵初值P₀后，在增益计算回路中，更新计算出滤波增益K_k和误差协方差阵P_k，在滤波计算回路中，结合滤波增益K_k，更新计算出滤波估计值X，随着时间的不断更新，P_k和也不断递推更新，因此能够得到系统的实时状态图5是按照本发明的优选实施例所构建的用观测器来估计SOFC电堆温度分布的示意图，如图5所示，电堆模型与观测器示意图，U为电堆输入，Z为电堆输出，输入和输出给进观测器中，通过观测器的预测和修正，来获得电堆无法直接测量的状态值实现电堆的状态估计，即电堆内部的温度分布。

本发明以通过有限元的节点建模方法，以5KW燃料电池为例，SOFC电堆由130片10cm×10cm规格的单电池组成。仿真中电堆初始条件为：电堆总电流I_tot＝30A；入口空气和氢气流量分别为入口空气和氢气的温度为

根据有限元的方法建立电堆模型后，进行线性化后，得到了矩阵

从而确定了观测器中的参数，对模型仿真后得到的出口固体层温度和空气层温度输入到观测器中，经过观测器中的迭代递推运算，获得电堆内部温度状态。

本例中，以SOFC电堆模型为比较对象，给观测器和模型以相同的输入。在任意给定电堆温度状态初始值及一步预测误差协方差阵初值之后，通过卡尔曼滤波算法的递推计算，温度观测器及电堆实际温度输出最后达到一致，实现实时温度预测；实际操作中，以实际电堆来替代电堆模型，测量得到实际的输入输出。同样地，给观测器以相同的输入，并把实际电堆输出反馈给观测器进行迭代计算。这样即可得到SOFC电堆实际运行时的内部温度分布。

本领域的技术人员容易理解，以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。