一种高精度雷达测距方法与流程

本发明属于雷达测量技术领域，具体涉及一种提高精度的雷达测距方法。

背景技术：

雷达测距具有稳定的测量性能和良好的环境适应性，受雨、雪、雾的干扰小，可以适应各种天气变化。使用雷达测距需要对电磁波在空气中传输的时间进行测量，从而根据测量的时间计算出电磁波在空气中传输的距离。但由于电磁波传播速度接近光速，近距离传输时相应的时间间隔很短，如果要达到厘米级的距离测量精度，那么时间测量的精度需要达到皮秒级，采用目前的技术手段难度较大。常用的时间测量方法有以下几种：

1.采用直接计数测量脉冲往返的时间，但该种方式精度较低，无法达到皮秒级要求。

2.采用微波计数器测量，其精度虽然已经可以达到皮秒的时间测量，但价格昂贵，很难普及。

可见，现有的几种方法存在精度不够或价格过高的缺陷。

技术实现要素：

为解决上述问题，本发明公开了一种雷达测距方法，通过变容二极管压振荡器在发射信号的周期和采样信号的周期间形成稳定且极小的时间差，利用发射脉冲信号和采样信号的微小周期差扩展放大电磁波传输时间以提高时间测量的精度，从而确保高精度的距离测量。

为了达到上述目的，本发明提供如下技术方案：

一种高精度雷达测距方法，包括如下步骤：

步骤a，设置两个周期相差很小的时钟信号，一个作为主时钟控制产生发射脉冲信号，周期为t1；另一个时钟用于产生周期为t2的采样信号，且t2>t1，则采样信号相对于发射脉冲信号的每次采样都将有一段延迟时间δt：

δt＝t2-t1(1)

采用两个完全相同的时钟电路来产生时钟信号，时钟电路中利用变容二极管压控振荡器来实现频率差的控制，利用电容和变容管与晶体组成谐振回路，首先调节一个时钟电路的电压，使该电路f1的频率达到一定值，其后通过调整另一个时钟电路的电压值来调整两个电路的频率差，从而形成稳定且极小的时间差δt；

步骤b，开启测量，首先使用采样信号对发射脉冲信号进行采样判断，当采样信号的上升沿检测到发射脉冲前沿时，确定发射开始时刻t1；此时开启对接收回波信号的采样判断，并对计数器清零开始计时，当检测到相应的接收回波前沿时确认回波接收时刻t2；此时切换到对发射脉冲信号进行采样判断，采样信号的上升沿检测到发射脉冲前沿时确认接收时刻t3并计数器清零；当次测量完成，同时开启下一次测量；

步骤c，根据测得的t1、t2、t3以及t1、t2，通过下式计算待测距离

式中c为电磁波在空气中传播的速度。

进一步的，所述步骤a中，时钟电路微调频率所需电压由处理器中的数模转换模块产生。

进一步的，所述数模转换模块为12位2通道电压输出数模转换模块。

进一步的，所述处理器为mcu。

进一步的，所述步骤c中进行多周期的连续测量，并通过测量的数据相互比较，去除部分偏差较大的测量值，最后计算测量有效值的平均值作为测量结果。

进一步的，所述步骤a中频率差为11hz～20hz。

与现有技术相比，本发明具有如下优点和有益效果：

对被测回波信号扩展后进行测量，并采用变容二极管压控振荡器来实现频率差的控制，使两个晶体振荡器产生稳定的周期差且周期可数控的信号，以提高测量的精度。本发明的时间测量精度可达到皮秒，即距离测量精度可达到厘米，测量精度高，且实现较容易，相比于较贵的测量精度达到皮秒的微波计数器，大大的降低了成本；相较于较难实现的基于fpga高精度的时间测量、时间电压转换等方法实现起来容易得多。

附图说明

图1为本发明测距示意图。

图2为本发明时钟产生电路原理图。

图3为变容二极管的电容特性与电压关系示意图。

图4为dac电压值对应的频率差。

图5为本发明测距时序图。

图6为周期差与时间的对应关系表。

具体实施方式

以下将结合具体实施例对本发明提供的技术方案进行详细说明，应理解下述具体实施方式仅用于说明本发明而不用于限制本发明的范围。

雷达回波为纳秒级窄脉冲，时间测量精度无法达到皮秒。由于测距时的回波信号是周期性的，故本发明对被测回波信号扩展后进行测量，并采用变容二极管压控振荡器来实现频率差的控制，使两个晶体振荡器产生稳定的周期差且周期可数控的信号，以提高测量的精度。

具体方法如下：

步骤a，如图1所示，设置两个周期相差很小的时钟信号，一个作为主时钟控制产生发射脉冲信号，周期为t1；另一个时钟用于产生周期为t2的采样信号，且t2>t1，则采样信号相对于发射脉冲信号的每次采样都将有一段延迟时间δt：

δt＝t2-t1(1)

要实现高精度测量的关键和难点在于发射信号的周期和采样信号的周期要形成稳定且极小的时间差δt，现在大多数方法是通过锁相和频率合成技术，实现起来比较复杂且很难达到需要的极小时间差。

本发明采用如图2所示的电路来产生时钟信号，电路中利用变容二极管压控振荡器来实现频率差的控制，实现简单且成本较低。控制电压改变变容二极管的等效电容从而改变晶体振荡器的频率，可使两个晶体振荡器产生稳定的周期差且周期可数控的信号。变容二极管是利用二极管在反向偏置条件下，势垒电容随外加电压而变化的一种器件，其结电容gj与外加电压的变化规律为

cj＝cj0/(1-vd/vb)ⁿ(2)

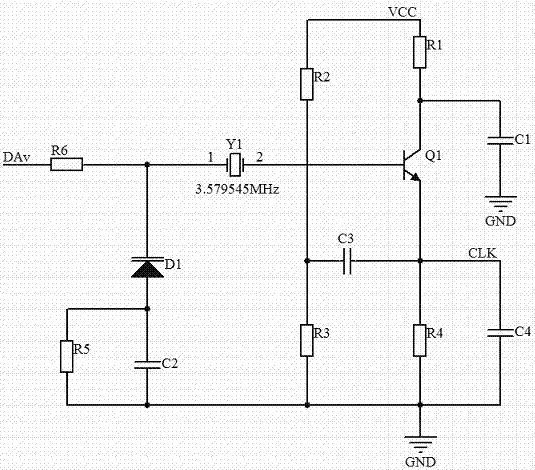
式中cj0是偏置为零时的电容值，vb是势垒电位差，n是电容变化指数。电容c3、c4和变容管与晶体组成谐振回路，晶体呈感性。控制电压dav改变了变容二极管的等效电容cj，从而改变了晶体振荡器的频率。变容二极管的电容特性与电压关系的如图3所示。

在电路中通过dav来调节电压，微调变容二极管d1两端的电压，从而微调d1的性能参数cj，以实现发射脉冲时钟和采样信号时钟的周期差。微调频率所需电压dav直接由mcu中的dac产生。mcu自带的dac转换模块是12位2通道电压输出的数模转换模块，软件选择12位输出；选择内部2.5v参考电压，可使dav在0v～2.5v之间调节。2通道电压输出可同时调整两路电路的电压值，从而较容易的控制频率差。实际应用中，使用两个完全相同的电路，首先调节dav1，使f1的频率达到3.579545mhz，其后通过调整dav2的电压值来调整两个电路的频率差。dac的电压值对应的频率差如图4所示。dav1和dav2由mcu的2路dac数模转换模块产生，扩时时间为测量值，频率差为计算值。

通过上述方法可以控制产生周期差约为δf＝11hz的两个时钟信号。

发射脉冲重复周期t1为：

采样脉冲重复周期t2为：

则其测量精度δt为：

δt＝t2-t1＝0.858ps(5)

因此，本发明测量精度可达皮秒级。根据测量精度公式，对应的理论距离测量精度为0.0258cm。但实际使用中，存在一定的噪声干扰，测量精度还受噪声等影响，会低于理论测量精度。

步骤b，开启测量，如图5所示，首先使用采样信号对发射脉冲信号进行采样判断，确认起始时刻。当采样信号的上升沿检测到发射脉冲前沿时，确定发射开始时刻t1。此时开启对接收回波信号的采样判断，并对计数器清零开始计时，当检测到相应的接收回波前沿时确认回波接收时刻t2。此时切换到对发射脉冲信号进行采样判断，采样信号的上升沿检测到发射脉冲前沿时确认接收时刻t3并计数器清零。当次测量完成，同时开启下一次测量。图5中，时序信号的前沿、后沿与检测到发射脉冲、接收回波的时刻保持同步，因此在时序信号高电平时间内对采样脉冲计数不存在量化误差，即理论上扩展系数k的测量误差趋于零。当不考虑电磁波在大气中的微小变化时，测距的相对误差主要取决于发射脉冲信号与采样脉冲信号周期差的相对误差。则时间测量精度为t2-t1，测量的时间值为t2-t1，即k(t2-t1)。经过上述方法对待测量的发射脉冲与接收回波之间的时间间隔t进行了一定比例的扩大，由于发射脉冲信号重复周期是固定了，可以通过对发射脉冲信号的扩时测量确认整个扩展系数n。为了减小误差可进行多周期的连续测量，并通过测量的数据相互比较，去除部分偏差较大的测量值，降低测量过程中随机干扰信号的影响。最后计算测量有效值的平均值，提高测量的精度。

步骤c，根据测得的t1、t2、t3以及t1、t2计算距离，推导距离换算公式的过程如下：假设一段传输延迟t经等效采样扩时测量后放大了n倍，即：

t2-t1＝nt(6)

在t1～t2时间段内，设检测到回波信号时计数器计数值为k，则有：

t2-t1＝kt2＝kt1+kδt＝kt1+t(7)

由式(6)、式(7)两式可得：

式(4-4)表明，待测时间间隔t被时间差所量化，k为待测的扩展系数，δt即采样测时的时间分辨力，在两时钟周期足够接近时，量化的分辨率可以达到很高。考虑测距时电磁波往返传播的路程，实际待测距离：

因此，在己知信号传播速度和两个时钟周期差的情况下，通过测量k可换算待测距离。当k＝1时，最小距离分辨力：

由式(10)可知，距离分辨力与发射脉冲信号和采样脉冲信号之间的周期差δt有关，因此可根据所需要实现的距离分辨力设定发射脉冲信号和采样脉冲信号的周期差。在传播速度一定的情况下，减小δt可以提高距离分辨力，不过相应的扩展系数k会随之变大，完成测量的时间也就相应增加。因此该算法是增加测量时间，提高了测量的精度。

由误差合成定理，对式(4-6)求全微分，而后用增量代替微分，可推导：

当不考虑电磁波在大气中的微小变化时，距离测量的相对误差主要取决于发射脉冲信号与采样脉冲信号周期差的相对误差。

在实际工程应用中，传输延迟t无法进行准确测量，故将公式(6)变形为

t3-t1即为发射脉冲展宽后的时间，其与发射脉冲的重复周期t1的比值为放大倍数n。

对回波信号展宽后的时间与回波传输时间关系为

由公式(12)、(13)可得

则待测距离为

式中c为电磁波在空气中传播的速度。

基于公式(15)计算待测距离d。

发射脉冲和采样脉冲的重复周期差可根据晶振的特性在一定的范围内调节，故其测量精度也能够在一定范围内进行调节。需结合实际使用情况，调节到适合的测量精度。根据公式(3)、(4)和(5)可计算得周期差对应的时间差及理论测量精度的关系，见图6所示，其中δf取值为11到20hz，δt取值为0.78皮秒到1.56皮秒之间。实际测量时的测量精度很大程度受系统噪声的影响。

本发明方案所公开的技术手段不仅限于上述实施方式所公开的技术手段，还包括由以上技术特征任意组合所组成的技术方案。应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也视为本发明的保护范围。