一种海面目标航向航速估算方法与流程

本发明涉及海面目标跟踪技术领域，特别涉及一种海面目标航向航速估算方法。

背景技术：

航向航速是海面目标的重要特征，能准确估计出航向航速对于海面目标的跟踪具有非常重要的意义。机载雷达对海面目标的跟踪同对空中目标的跟踪相比存在很多差异，其探测性能面临一些新的挑战，其中由于海面目标运动速度较慢，短时间内很难运动出机载雷达的最小分辨单元，导致目标航向航速估计的收敛速度较慢，不利于指挥者快速做出决策。此外，受机载雷达测量精度的影响，海面目标航向估计对方位角量测的随机偏差较为敏感，当方位角测量出现小幅波动时，会造成海面目标航向估计的震荡，精度难以保证。因此如何实现对海面目标航向航速的精确估计成为亟待解决的问题。

为了提高复杂环境下海面目标航向航速的估计精度，目前经常使用的方法可以主要分为两类：

第一类方法是先通过数据关联完成观测数据与目标间的匹配，再利用非线性滤波技术完成对海面目标航向航速的估计。在非线性滤波领域已有许多经典算法，例如扩展卡尔曼滤波算法(EKF)，无迹卡尔曼滤波算法(UKF)及容积卡尔曼滤波算法(CKF)等。然而，这些滤波算法都是高斯滤波算法(GF)基于不同数值计算方法的近似，在量测高精度、系统高维数、复杂强非线性的情况下往往不能很好的近似系统状态的后验概率密度函数，导致滤波精度大大降低。

第二类方法是先对机载雷达测量的方位角及径向距离做平滑处理，降低测量波动对目标航向的影响，再根据机载雷达和目标的运动几何关系解算出海面目标的航向航速信息。然而这种方法仅在海面目标做匀速直线运动时解算效果才较好，当海面目标发生机动(如协同转弯)时，所建目标的动力学模型与目标的实际运动模式不匹配，最终导致对海面目标的跟踪丢失。

针对机载雷达不同的测量精度及海面目标不同的运动场景，不同的滤波算法滤波性能不同，如何获得具有高精度、高鲁棒性、同时保证实时性的非线性滤波算法是海面目标航向航速估计技术的关键所在。

技术实现要素：

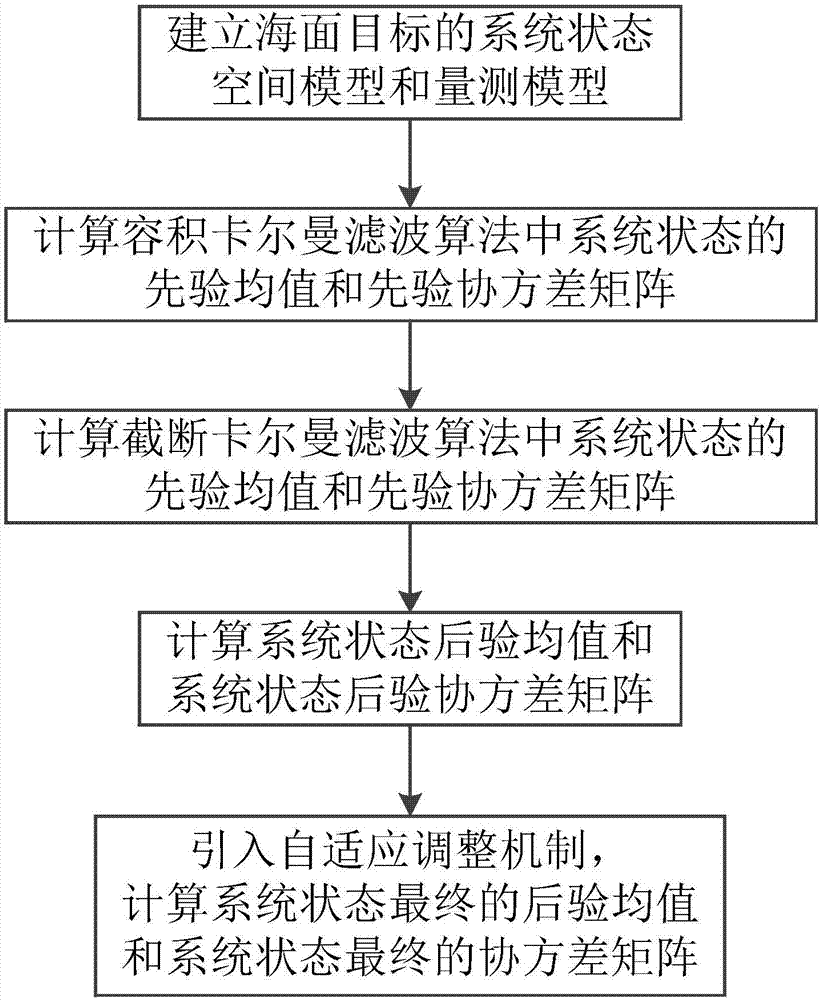
为克服上述现有技术存在的至少一种缺陷，本发明提供了一种海面目标航向航速估算方法，包括如下步骤：

步骤一，根据海面目标的运动状态建立出相应的系统状态空间模型，并根据机载雷达的测量原理建立量测模型，所述系统状态方程和所述量测方程如公式(1)所示：

公式(1)中k为时刻，k-1为k时刻的前一时刻，f()表示系统状态转移函数，h()表示量测函数；

xk表示k时刻系统状态向量，其取值范围为nx为状态维数，R为实数；

Zk表示k时刻外部量测向量，其取值范围为nz为量测维数；

wk-1是系统噪声，其取值范围为nw是系统噪声维数；

vk是量测噪声，其取值范围为nv是量测噪声维数；

步骤二，计算容积卡尔曼滤波算法中系统状态的先验均值及先验协方差矩阵P0,k|k-1，其计算公式如公式(2)所示：

公式(2)中m是容积点个数，是通过状态方程传播的容积点，Qk-1是系统噪声协方差矩阵，上标T表示矩阵转置；

步骤三，计算截断卡尔曼滤波算法中系统状态的先验均值及先验协方差矩阵P1,k|k-1，其计算公式如公式(3)所示：

公式(3)中h^-1()表示对量测函数求逆，Hk是量测函数h( )在k时刻的雅克比矩阵，上标-1表示求逆，上标T表示矩阵转置，Rk是量测噪声协方差矩阵；

步骤四，根据容积卡尔曼滤波算法量测更新框架，并根据步骤二中算出的和P0,k|k-1以及步骤三中算出的和P1,k|k-1，通过公式(4)得到系统状态后验均值和系统状态后验协方差Ph,k|k，其中h为滤波算法选择参数，h＝0时的参数为容积卡尔曼滤波算法的参数，h＝1时的参数为截断卡尔曼滤波算法的参数，如为容积卡尔曼滤波算法的系统状态后验均值，P1,k|k为截断卡尔曼滤波算法的系统状态后验协方差；

公式(4)中Wh,k是卡尔曼滤波增益，上标T表示矩阵转置，Zh,k是量测值，是量测先验均值，Ph,zz,k|k-1是量测的自相关先验协方差矩阵，其中zz表示自相关，此处h同为波算法选择参数，如W0,k为容积卡尔曼滤波算法的卡尔曼滤波增益，P1,zz,k|k-1为截断卡尔曼滤波算法的卡尔曼滤波增益；

步骤五，引入自适应调整机制，通过公式(5)计算系统状态最终的后验均值通过公式(6)计算系统状态最终的协方差矩阵Pk|k，得到目标

公式(5)和公式(6)中，上标T表示矩阵转置，α是自适应变换参数，α的计算公式如公式(7)所示：

公式(7)中，γ是预先设定的预调整参数，

tr(P0,k|k-1)是P0,k|k-1的迹，tr(P1,k|k-1)是P1,k|k-1的迹。

优选的，步骤一中的状态空间模型包括匀速直线运动模型(CV模型)、匀加速直线运动模型(CA模型)、协同转弯模型(CT模型)。

优选的，步骤一中的量测模型包括海面目标的距离以及方位角。

优选的，公式(1)中的k时刻系统状态向量xk包括目标的位置、速度和加速度，k时刻外部量测向量Zk包括径向距离、方位角和俯仰角。

优选的，步骤一中，wk-1和vk互不相关且均为服从高斯分布的零均值高斯白噪声，且wk-1～N(0,Qk-1)，vk～N(0,Rk)，其中Qk-1是系统噪声协方差矩阵，Rk是量测噪声协方差矩阵。

本发明提供的一种海面目标航向航速估算方法，对传统非线性高斯滤波器的时间更新阶段进行了改进，对系统状态的先验概率密度函数做了截断处理，增加了对状态先验估计的置信程度，降低了系统状态的先验不确定性，同时引入了一种自适应调整机制，将容积卡尔曼滤波算法和截断卡尔曼滤波算法通过一个自适应变化的参数有机地结合起来，使其能够根据外部量测信息的变化动态地调整二者相对权值的大小，减轻了量测非线性及高精度对滤波器量测更新阶段的影响，解决了传统非线性高斯滤波器在量测高精度、系统高维数、复杂强非线性情况下对系统状态后验概率密度函数近似精度不高这一问题，提高了复杂环境下海面目标航向航速的估计精度。

附图说明

图1是海面目标航向航速估算方法的流程图；

图2是海面目标运动轨迹曲线图；

图3是多种滤波算法估算海面目标航向航速的均方根误差曲线图。

具体实施方式

为使本发明实施的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行更加详细的描述。在附图中，自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。所描述的实施例是本发明一部分实施例，而不是全部的实施例。下面通过参考附图描述的实施例是示例性的，旨在用于解释本发明，而不能理解为对本发明的限制。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

下面通过具体的实施例对本发明作进一步详细的描述。

具体实施例：

考虑海面目标在二维平面内做协同转弯机动的情况。假设系统噪声和量测噪声均服从高斯分布，载机做匀速直线运动，海面目标运动轨迹如图2所示；

目标状态向量uk和分别表示k时刻海面目标在X轴的位置和速度，yk和分别表示k时刻海面目标在Y轴的位置和速度。目标运动模型采用协同转弯(CT)模型进行表示：

其中表示高斯噪声，

其协方差矩阵为因此，系统噪声的协方差矩阵Qk-1可以表示为：

其中ω表示海面目标转弯角速率，T表示采样周期，在二维情况下传感器的量测方程为Zk＝h(xk)+vk，其中Zk＝[rk θk]^T，rk表示k时刻测量的海面目标径向距离，θk表示k时刻测量的海面目标方位角，vk表示零均值高斯量测噪声，其与wk-1相互独立；

量测噪声矩阵可以表示为其中和分别表示海面运动目标径向距离和方位角的测量误差方差，而量测函数为：

其中upk和ypk分别表示k时刻载机在X轴和Y轴的位置。

仿真中基本参数设置如下：

初始时刻载机位置(up0,yp0)＝(0m,0m)，

载机速度(vpu,vpy)＝(120m/s,0m/s)，

目标初始位置(u0,y0)＝(45km,60km)，

航向φ＝45°，

目标速度

仿真时间900s，雷达采样周期为T＝1s，

雷达方位分辨率为距离分辨率为σr＝1m。

多种滤波算法对海面目标航向航速的估算结果如表2所示，估算结果的曲线图如图3及所示，表2和图3中的滤波算法包括容积卡尔曼滤波算法(CKF)、无迹卡尔曼滤波算法(UKF)以及本发明提供的航向航速估算方法(TACKF)。

表2多种滤波算法估算海面目标航向航速结果表

从图3的误差曲线图中可以看出，本发明提供的航向航速估算方法(TACKF)的估算精度要明显高于容积卡尔曼滤波算法(CKF)和无迹卡尔曼滤波算法(UKF)，表明当海面目标作协同转弯运动且雷达距离、方位测量精度较高时，本发明提供的航向航速估算方法能够更有效的逼近系统状态的后验概率密度函数，提高了海面目标航向航速的估算精度。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到的变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应以所述权利要求的保护范围为准。