一种声呐扇形图的转换更新方法与流程

本发明属于声呐图像处理领域，主要涉及是测试过程中瀑布图到扇形图的快速转换，并实时动态的更新。

背景技术：

多波束测深主要是利用接收换能器接收到发射换能器发出的声波经海底散射的回波信号，然后经过数据处理，把扫描区域的海底信息呈现在上位机上。在声呐图显示过程中，波束形成后的数据是(r,θ)坐标下的复数阵，由于数据是在极坐标空间下，若直接进行成像显示不符合人眼视觉习惯，因此需要将极坐标下的瀑布图转换为笛卡尔坐标下(x,y)的扇形图，从而显示到上位机界面上，供测量员进行观察和分析。

在测量过程中，数据是实时动态更新的，而坐标转换过程中，是大量的三角函数转换，比较耗时，如何实时动态更新成为成为关键。坐标间的变换关系为：

在进行坐标变换主要是对声呐数据的插值计算，坐标转换主要有两种途径，第一种：把波束形成后的极坐标下的所有点都转换为笛卡尔坐标下的点，然后在笛卡尔坐标下对数据进行插值计算，当测量深度增大时，数据量也随之变多，运算量也随之变大，而且在坐标变化过程中是大量的三角变换，不易满足实时动态更新的要求；第二种，只计算笛卡尔坐标下所需要点的像素值，将笛卡尔空间下的数据变换到极坐标，在极坐标下进行像素点的插值计算。

声呐图像的显示利用FPGA进行扇形变换，由于大量的三角函数运算比较占用硬件资源，可以有两种处理方式。第一种：利用空间换时间的思想，把三角函数的值事先存在硬件存储器中，需要时直接调用，陈靖宇【陈靖宇，高分辨率雷达显示坐标变换及相关设计，舰船电子对抗，2001】利用三角函数的周期性和对称性，EPROM存的是第一象限的进位值，从而降低存储器的容量要求。但仍需消耗硬件资源进行存储，有的系统配置无法满足需求；第二种：利用时间换取空间的思想，利用迭代逼近算法计算三角函数值，但会造成迭代次数增加，从而造成计算时间的增加，例如谈宜育等人【谈宜育，卞文兵，一种基于CORDIC算法的坐标变换电路，数据采集与处理，2001】利用CORDIC算法的坐标变换电路实现了对B超图像的变换，利用高的数据量化位来保证精度。这些都是通过硬件实现，开发周期比较长，可以把图像声呐处理部分放在上位机上处理，借助并行优化技术，加速算法处理速度。

技术实现要素：

本发明的目的旨在解决上述问题，从而提供一种声呐扇形图的转换更新方法。该方法包括以下步骤：

a、将波束形成后的复数矩阵进行求模、转置处理，然后建立像素点索引，所述像素点为转置处理后矩阵中的每个元素；

b、根据声呐图像的开角计算出期望成像的扇形图的宽w_期和高h_期；

c、根据计算出的w_期和h_期，为扇形图的x，y坐标赋值；

d、根据(x，y)的坐标，计算出极坐标空间下对应的(r,θ)；

e、根据计算出的(r,θ)，在步骤a中的原始瀑布图里，通过步骤a中建立的索引，在所需要的点(r,θ)附近处进行双线性插值计算，算出笛卡尔坐标系下的点(x₀,y₀)映射到极坐标系下的点(r₀,θ₀)的像素值；

f、重复步骤e完成笛卡尔坐标系下点阵内的所有点与极坐标系下的点的映射，并插值计算出各个点的像素值，即获得笛卡尔坐标系下的声呐扇形图；

g、随着深度变化，更新步骤d中y坐标的赋值，然后重复步骤d～f，实现扇形图的更新。

进一步地，所述步骤a中建立像素点索引具体包括:

波束形成后的复数矩阵是等角模式矩阵时：

将转置处理后矩阵中各元素的对应的波束角度由θ_m，n来表示，θ_m，n代表矩阵中第n个时间片(行)第m(列)元素对应的波束角度，将各元素对应的波束角度通过公式(θ_m，n+0.5*开角)/步长换算为整数，每个整数即为索引号；

波束形成后的复数矩阵是等距模式矩阵时：

通过像素点插值计算出一个等角的瀑布图矩阵；将等角的瀑布图矩阵进行转置处理；将转置处理后矩阵中各元素的对应的波束角度由θ_m，n来表示，θ_m，n代表矩阵中第n个时间片(行)第m(列)元素对应的波束角度，将各元素对应的波束角度通过公式(θ_m，n+0.5*开角)/步长换算为整数，每个整数即为索引号。

进一步地，所述声呐图像的开角为120～140度。

进一步地，所述步骤b计算期望成像的扇形图的宽高具体为：

当期望的高度<期望的宽度时，设定一高度值作为图像期望的高度h_期，期望的图像宽度w_期通过公式w_期＝2*h_期*cos(0.5*(180-openangle)*PI/180)计算获得，其中openangle为声呐图像的开角；

当期望的高度>期望的宽度时，设定一宽度值作为图像期望的宽度w_期，期望的图像高度h_期通过公式h_期＝(0.5*w_期)/cos(0.5*(180-openangle)*PI/180)计算获得，其中openangle为声呐图像的开角。

进一步地，所述步骤c具体包括：

根据计算出的h_期，赋值h_期行，每行的纵坐标y＝i*k1，i的取值为从1～h_期之间的自然数，k1为比例系数，其通过公式k1＝l_通/h_期计算而得，式中，l_通为波束形成后的每通道数据长度；

每行的横坐标x是以-1*l_通*k2为初值，步长为2*l_通*k2/w_期的等差数列，其中，l_通为波束形成后的每通道数据长度，k2为x方向的比例系数，其通过公式k2＝w_期/h_期计算而得。

进一步地，所述步骤d通过下列公式计算而得：

进一步地，所述步骤e具体包括：判断计算出的(r,θ)的角度是否在声呐图像开角范围内，若不在，则该点的像素值赋值为0；若在，则通过步骤a中建立的索引，插值计算出该点的像素值。

进一步地，在所述步骤f和步骤g之间还包括：

h、通过intel的图像拉伸函数对步骤f形成后的声呐扇形图进行宽度和高度的放大；

进一步地，在所述步骤f和步骤g之间还包括：

i、对步骤f形成的声呐扇形图的像素点的幅值统一调整，以使得扇形图亮度高于背景图。

进一步地，所述步骤f通过openMP并行优化函数进行优化计算。

本发明的声呐扇形图的转换更新方法通过基于上位机进行建立索引，然后利用建立的索引进行图像像素点的插值计算，实现了瀑布图到扇形图的快速转换，避免了FPGA等硬件繁琐的三角或反三角函数变换，提高了运算效率和准确率，节省了时间。

附图说明

图1为本发明声呐扇形图的转换更新方法的一个实施例图；

图2为本发明声呐扇形图的转换更新方法的另一个实施例图；

图3为本发明声呐扇形图的转换更新方法中的瀑布图；

图4为本发明声呐扇形图的转换更新方法中的最终形成的扇形图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。需要说明的是，附图仅为示例性说明，并未按照严格比例绘制，而且其中可能有为描述便利而进行的局部放大、缩小，对于公知部分结构亦可能有一定缺省。

图1为本发明声呐扇形图的转换更新方法的一个实施例图。

如图1所示，本发明提供了一种声呐扇形图的转换更新方法。该方法主要包括以下步骤：

在步骤101中，将波束形成后的复数矩阵进行求模、转置处理，然后建立像素点索引，其中像素点为转置处理后矩阵中的每个元素。其中，波束形成后的复数矩阵求模、转置后的瀑布图可参见图3。

具体地，本步骤中复数矩阵的转置处理是：将波束形成后的复数矩阵先进行求取模值变为实数矩阵，然后再对实数矩阵进行转置。

本步骤中的建立像素点索引具体是：由于波束形成后的复数矩阵可能是等角模式矩阵，也可能是等距模式矩阵，那么可分为两种情况进行说明：

第一种情况，波束形成后的复数矩阵是等角模式矩阵时：则将转置处理后实数矩阵中各元素的对应的波束角度用θ_m，n来表示，θ_m，n代表矩阵中第n个时间片(行)第m(列)元素对应的波束角度，将各元素对应的波束角度通过公式(θ_m，n+0.5*开角)/步长换算为整数，每个整数即为索引号。需要索引的时候，直接可用索引号，调取该索引号对应的像素值。其中，转置后实数矩阵中每个元素都有三个值，x、y和该点对应的像素值G。比如说，声纳图像开角为130度，波束形成转置后，假设图像的第一行y坐标是1，x坐标是-64.5到65，间隔数0.5度，一共是260个(x，y)坐标，每个(x，y)坐标都有一个像素值G，由于x坐标不是整数，(-64.5:0.5:65)这个x坐标先都加上0.5*130；然后在都除以0.5，就把x的坐标由原来的(-64.5:0.5:65)变为(1:1:260)，原来第一个点是(-64.5，1)对应的像素是G，那么现在(1，1)就获得这个像素点的值了。即完成了复数矩阵中第一个元素从原来坐标是(-64.5，y，G)，转变为(1，y，G)。这样处理主要是为了获得G的值(像素值)方便。

第二种情况，若波束形成后的复数矩阵是等距模式矩阵时：

通过像素点插值计算出一个等角的瀑布图矩阵；将等角的瀑布图矩阵进行转置处理；将转置处理后矩阵中各元素的对应的波束角度由θ_m，n来表示，θ_m，n代表矩阵中第n个时间片(行)第m(列)元素对应的波束角度，将各元素对应的波束角度通过公式(θ_m，n+0.5*开角)/步长换算为整数，每个整数即为索引号。需要索引的时候，直接可用索引号，调取该索引号对应的像素值。其中，转置后实数矩阵中每个元素都有三个值，x、y和该点对应的像素值G。具体例子可参见等角模式矩阵中例子，在此不一一赘述。

在步骤102中，根据声呐图像的开角计算出期望成像的扇形图的宽w_期和高h_期。

其中，声呐图像的开角为步骤101中复数矩阵中每个元素对应的角度所形成的一个开角范围，该范围一般为120度至140度，优选为130度。

本步骤中计算出期望的扇形图的宽w_期和高h_期具体可参见如下：

当期望的高度<期望的宽度时，设定一高度值作为图像期望的高度h_期，期望的图像宽度w_期通过公式w_期＝2*h_期*cos(0.5*(180-openangle)*PI/180)计算获得，其中openangle为声呐图像的开角，比如上述的120度至140度。

当期望的高度>期望的宽度时，设定一宽度值作为图像期望的宽度w_期，期望的图像高度h_期通过公式h_期＝(0.5*w_期)/cos(0.5*(180-openangle)*PI/180)计算获得，其中openangle为声呐图像的开角，比如上述的120度至140度。

在步骤103中，根据计算出的w_期和h_期，为扇形图的x，y坐标赋值。

本步骤中为扇形图的x，y坐标赋值具体可参见如下：

根据计算出的h_期，赋值h_期行，每行的纵坐标y＝i*k1，i的取值为从1～h_期之间的自然数，k1为比例系数，其通过公式k1＝l_通/h_期计算而得，式中，l_通为波束形成后的每通道数据长度。

每行的横坐标x是以-1*l_通*k2为初值，步长为2*l_通*k2/w_期的等差数列，其中，l_通为波束形成后的每通道数据长度，k2为x方向的比例系数，其通过公式k2＝w_期/h_期计算而得。

在步骤104中，根据(x，y)的坐标，计算出极坐标空间下对应的(r,θ)。

本步骤中，(x，y)的坐标可通过换算公式计算出极坐标空间下对应的(r,θ)。

在步骤105中，根据计算出的(r,θ)，在步骤101中的原始瀑布图里，通过索引，在所需要的点(r,θ)附近处进行双线性插值计算，算出笛卡尔坐标系下的点(x₀,y₀)映射到极坐标系下的点(r₀,θ₀)的像素值；其中(x₀,y₀)为步骤104中(x，y)的一个元素。

本步骤具体可参见如下：

对从(x₀,y₀)转换后的(r₀,θ₀)进行转换,然后判断该角度是不是在开角范围内，当坐标点不在开角范围内，像素值赋值为0，当位于开角范围内，利用步骤101中建立的索引，插值计算出该点的像素值。

比如开角130度，角度范围是-64.5到65度，角度间隔为0.5度，(r₀,θ₀)为从(x₀,y₀)转化的坐标，对坐标中的角度θ₀通过步骤101中的公式(θ₀+0.5*130)/0.5获得和步骤101一样的到坐标值环境，但是通过公式(θ₀+0.5*130)/0.5获得的不一定是整数，且该点没有像素值，要获得该点像素值需要用步骤101中的建立的索引插值计算获得该点的像素值。比如说θ₀现在换算出是2.5，那么就可利用步骤101中的索引号2和3计算出2.5所对应的像素值。

在步骤106中，重复步骤105，完成笛卡尔坐标系下点阵内的所有点与极坐标系下的点的映射，并插值计算出各个点的像素值，即获得笛卡尔坐标系下的声呐扇形图。转换后的扇形图可参见图4。

在步骤107中，随着深度变化，更新步骤103中y坐标的赋值，然后重复步骤104～106，实现扇形图的更新。

以上对本发明提供的声呐扇形图的转换更新方法的一个实施例进行了详细说明，以下将对本发明的声呐扇形图的转换更新方法的另一个实施例进行说明。

请参阅图2，图2为本发明声呐扇形图的转换更新方法的另一个实施例图，如图2所示，本发明声呐扇形图的转换更新方法具体包括如下步骤：

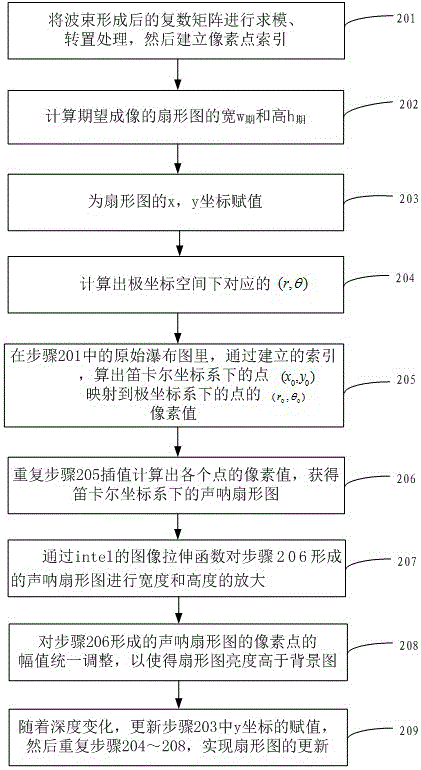
在步骤201中，将波束形成后的复数矩阵进行求模、转置处理，然后建立像素点索引，其中像素点为转置处理后矩阵中的每个元素。其中，波束形成后的复数矩阵求模、转置后的瀑布图可参见图3。

具体地，本步骤中复数矩阵的转置处理是：将波束形成后的复数矩阵先进行求取模值变为实数矩阵，然后再对实数矩阵进行转置。

本步骤中的建立像素点索引具体是：由于波束形成后的复数矩阵可能是等角模式矩阵，也可能是等距模式矩阵，那么可分为两种情况进行说明：

第一种情况，波束形成后的复数矩阵是等角模式矩阵时：则将转置处理后实数矩阵中各元素的对应的波束角度用θ_m，n来表示，θ_m，n代表矩阵中第n个时间片(行)第m(列)元素对应的波束角度，将各元素对应的波束角度通过公式(θ_m，n+0.5*开角)/步长换算为整数，每个整数即为索引号。需要索引的时候，直接可用索引号，调取该索引号对应的像素值。其中，转置后实数矩阵中每个元素都有三个值，x、y和该点对应的像素值G。比如说，声纳图像开角为130度，波束形成转置后，假设图像的第一行y坐标是1，x坐标是-64.5到65，间隔数0.5度，一共是260个(x，y)坐标，每个(x，y)坐标都有一个像素值G，由于x坐标不是整数，(-64.5:0.5:65)这个x坐标先都加上0.5*130；然后在都除以0.5，就把x的坐标由原来的(-64.5:0.5:65)变为(1:1:260)，原来第一个点是(-64.5，1)对应的像素是G，那么现在(1，1)就获得这个像素点的值了。即完成了复数矩阵中第一个元素从原来坐标是(-64.5，y，G)，转变为(1，y，G)。这样处理主要是为了获得G的值(像素值)方便。

第二种情况，若波束形成后的复数矩阵是等距模式矩阵时：

通过像素点插值计算出一个等角的瀑布图矩阵；将等角的瀑布图矩阵进行转置处理；将转置处理后矩阵中各元素的对应的波束角度由θ_m，n来表示，θ_m，n代表矩阵中第n个时间片(行)第m(列)元素对应的波束角度，将各元素对应的波束角度通过公式(θ_m，n+0.5*开角)/步长换算为整数，每个整数即为索引号。需要索引的时候，直接可用索引号，调取该索引号对应的像素值。其中，转置后实数矩阵中每个元素都有三个值，X、Y和该点对应的像素值G。具体例子可参见等角模式矩阵中例子，在此不一一赘述。

在步骤202中，根据声呐图像的开角计算出期望成像的扇形图的宽w_期和高h_期。

其中，声呐图像的开角为步骤201中复数矩阵中每个元素对应的角度所形成的一个开角范围，该范围一般为120度至140度，优选为130度。

本步骤中计算出期望的扇形图的宽w_期和高h_期具体可参见如下：

当期望的高度<期望的宽度时，设定一高度值作为图像期望的高度h_期，期望的图像宽度w_期通过公式w_期＝2*h_期*cos(0.5*(180-openangle)*PI/180)计算获得，其中openangle为声呐图像的开角，比如上述的120度至140度。

当期望的高度>期望的宽度时，设定一宽度值作为图像期望的宽度w期，期望的图像高度h_期通过公式h_期＝(0.5*w_期)/cos(0.5*(180-openangle)*PI/180)计算获得，其中openangle为声呐图像的开角，比如上述的120度至140度。

在步骤203中，根据计算出的w_期和h_期，为扇形图的x，y坐标赋值。

本步骤中为扇形图的x，y坐标赋值具体可参见如下：

根据计算出的h_期，赋值h_期行，每行的纵坐标y＝i*k1，i的取值为从1～h_期之间的自然数，k1为比例系数，其通过公式k1＝l_通/h_期计算而得，式中，l_通为波束形成后的每通道数据长度。

每行的横坐标x是以-1*l_通*k2为初值，步长为2*l_通*k2/w_期的等差数列，其中，l通为波束形成后的每通道数据长度，k2为x方向的比例系数，其通过公式k2＝w_期/h_期计算而得。

在步骤204中，根据(x，y)的坐标，计算出极坐标空间下对应的(r,θ)。

本步骤中，(x，y)的坐标可通过换算公式计算出极坐标空间下对应的(r,θ)。

在步骤205中，根据计算出的(r,θ)，在步骤201中的原始瀑布图里，通过索引，在所需要的点(r,θ)附近处进行双线性插值计算，算出笛卡尔坐标系下的点(x₀,y₀)映射到极坐标系下的点(r₀,θ₀)的像素值；其中(x₀,y₀)为步骤204中(x，y)的一个元素。

本步骤具体可参见如下：

对从(x₀,y₀)转换后的(r₀,θ₀)进行转换,然后判断该角度是不是在开角范围内，当坐标点不在开角坐标范围内，像素值赋值为0，当位于开角范围内，利用步骤201中建立的索引，插值计算出该点的像素值。

比如开角130度，角度范围是-64.5到65度，角度间隔为0.5度，(r₀,θ₀)为从(x₀,y₀)转化的坐标，对坐标中的角度θ₀通过步骤101中的公式(θ₀+0.5*130)/0.5获得和步骤201一样的到坐标值环境，但是通过公式(θ₀+0.5*130)/0.5获得的不一定是整数，且该点没有像素值，要获得该点像素值需要用步骤201中的建立的索引插值计算获得该点的像素值。比如说θ₀现在换算出是2.5，那么就可利用步骤201中的索引号2和3计算出2.5所对应的像素值。

在步骤206中，重复步骤205，完成笛卡尔坐标系下点阵内的所有点与极坐标系下的点的映射，并插值计算出各个点的像素值，即获得笛卡尔坐标系下的声呐扇形图，效果图可参见图4。

在步骤207中，通过intel的图像拉伸函数对步骤206形成后的声呐扇形图进行宽度和高度的放大。

在步骤208中，对步骤206中形成的声呐扇形图的像素点的幅值统一调整，以使得扇形图亮度高于背景图，即使扇形图图像明显区别于背景图。

在步骤209中，随着深度变化，更新步骤203中y坐标的赋值，然后重复步骤204～208，实现扇形图的更新。

以上对本发明提供的声呐扇形图的转换更新方法的另一个实施例进行了详细说明。

综上，本发明的声呐扇形图的转换更新方法通过基于上位机进行建立索引，然后利用建立的索引进行图像像素点的插值计算，实现了瀑布图到扇形图的快速转换，避免了FPGA等硬件繁琐的三角或反三角函数变换，提高了运算效率和准确率，节省了时间。

以上所述的具体实施方式，对本发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本发明的具体实施方式而已，并不用于限定本发明的保护范围，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。