一种新型光谱多元分析分类与识别方法及其用途与流程

本发明涉及光谱分析领域，可用于石化、烟草、医药、环境、食品检测等领域。本发明针对SIMCA方法因欧氏距离导致分类不够精确的问题，采用了马氏距离来代替欧式距离进行预测，是一种改进的SIMCA方法。

背景技术：

分子光谱(红外、近红外和拉曼)从分子水平上反映了物质组成与结构信息,紫外，LIBS、X荧光等波谱则从电子或原子水平上反映物质组成和结构的信息。随着光谱仪器技术的发展，这些光谱的获取也越来越容易，不仅速度快，且大多无损，因此，光谱已经成为分析技术的理想信息载体。复杂物质光谱是其组分光谱的叠加，共存组分信息干扰使得分析难度增加，多元分析方法则是用来提取其有用信息的有力工具。将光谱和多元分析方法结合起来，称之为现代光谱分析技术，可以实现复杂体系的定性和定量分析，具有快速、无损和高通量的等优点，已广泛应用于石化、烟草、医药、环境、食品检测等领域，对工业生产过程质量和成本控制以及流通领域质量监督等具有不可或缺的重要作用。

现代光谱分析方法包括定性和定量。其中，光谱定性分析也称判别分析，主要用于两个方面。一是用于判别样品的种类，等级，来源及真伪等，二是判别待分析样品是否落在定量分析模型范围之内，即用于确定多元定量分析模型的适用范围，对于保障光谱多元定量分析结果的准确性具有关键作用。

目前光谱多元分析中常用的分类方法主要包括：线性学习机(Linear Learning Machine)、K-最近邻法(K-Nearest Neighbors Discrimination Method,KNN)、主成分分析(Principal Component Analysis，PCA)、马氏距离(Mahalanobis Distance,MD)法、判别分析法(Discrimination Analysis,DA)、SIMCA方法、聚类分析、支持向量机等。在实际分析中普遍认为SIMCA方法是应用最广和最成熟的方法，被MATLAB软件列入工具箱，在科学研究中也是使用频率最高的。

SIMCA方法是有监督的分类方法，分别对各类样品光谱进行主成分分析，建立各类样本的主成分光谱空间，分别采用主成分得分和光谱残差信息及F检验构造两个统计量T²和Q(残差)，作为样本分类的新属性，然后，使用这两个属性计算样本到各类样品主成分光谱空间的欧氏距离，通过比较待测样品到各类样品主成分光谱空间的欧氏距离和设定阈值，实现样本的有效分类与识别。大量光谱应用结果表明，SIMCA方法分类可以获得很好的效果。但是，对于区分成分相近又存在着微小差异的样本，SIMCA方法分类的效果也不理想。在光谱主成分分析分类中常用马氏距离，以马氏距离描述的分布在几何学上呈椭圆状。相比欧式距离，用马氏距离描述实际样本空间分布将更贴近于实际。为此，本发明提出一种改进的SIMCA新方法，采用马氏距离来代替欧氏距离进行预测，改善SIMCA方法的分类精度。

技术实现要素：

针对SIMCA方法难以区分成分相近又存在着微小差异的样本的问题，本发明提供了一种改进的SIMCA方法。其关键点在于：在SIMCA建立好模型之后，采用马氏距离来代替欧氏距离进行预测。

本发明所述一种新型光谱多元分析分类与识别方法，包括以下步骤：

(1)样本制备与光谱采集：收集待检测材料，根据材料特性，将待检测材料加工处理制成样本，使得光谱仪能采集到样本的光谱数据；

(2)样本光谱数据采集与处理：用光谱仪器对步骤(1)中制得的样本进行光谱测量，可获得由步骤(1)制得的样本的光谱数据组成的样本光谱数据集Sm，，并利用SG平滑方法消除样本光谱数据集Sm中光谱数据的高频噪音，然后用一阶求导方法消除样本光谱数据集Sm中光谱数据的基线漂移，接着对样本光谱数据集Sm中光谱数据进行均值中心化处理；

(3)建立多元校正模型：将经过步骤(2)处理后的样本光谱数据集Sm分为校正集Smc和验证集Smv，校正集Smc由具有的样本光谱数据组成且占样本光谱数据集Sm的光谱数据的80％；分别对校正集Smc中的每类样本建立主成分模型，并根据Hotelling T2检验计算T²的临界值根据建模样本集的二次分布结果近似出残差阈值Q；其中，建模样本集的二次分布结果为校正集Smc的高斯分布结果；

(4)预测：根据主成分模型的最佳主成分数A计算验证集Smc中样本的T²和残差S_i的值，通过临界值和Q计算验证集Smv中的样本到主成分模型的马氏距离，并根据最小的马氏距离值判别待测样本的类别；

(5)评价：以步骤(3)中所得到的验证集Smv对不同方法预测的结果进行评价，以主成分模型的预测准确率和错误样本个数为指标，评价方法的优劣，其中，预测准确率的计算公式如下：

下面对本发明进行进一步的说明：

上述方法中，在步骤(3)中，分别对校正集Smc中的每类样本建立主成分模型，并根

据Hotelling T2检验计算T²的临界值根据建模样本集的二次分布结果近似出残差的

阈值Q，具体步骤如下：

(3.1)对于每一个校正集Smc，将校正集Smc中样本光谱数据按类别分开并进行编号，然后分别对每类样本光谱数据建立PCA模型；以其中的一类光谱数据X为例，建立PCA模型：

其中为样本均值，T为得分矩阵，P为载荷矩阵；

(3.2)用交叉验证计算预测误差平方加和PRESS，根据PRESS随主成分数变化曲线确定步骤(3.1)中所建PCA模型的最佳主成分数A；

(3.3)根据步骤(3.2)中确定的最佳主成分数A建立主成分模型其中X为样本均值，T为得分矩阵，P为载荷矩阵，E为残差矩阵；

(3.4)根据Hotelling T2检验，利用步骤(3.2)中确定的最佳主成分数A，计算T²的临

界值

(3.5)根据建模样本集的二次分布结果，利用协方差矩阵，近似出残差阈值Q。

上述方法中，步骤(4)具体包括如下步骤：

(4.1)根据步骤(3.2)中确定的最佳主成分数A，计算验证集Smc中样本的T_i²和残差S_i的值；

(4.2)根据步骤(3.1)中T²的临界值和残差阈值Q，对验证集Smv中的样本i进行特征提取，于是样本i可表示为

(4.3)计算样本i到步骤(3.1)中所建PCA模型的中心(O＝{0,0})的马氏距离；

(4.4)如果样本i在哪一类PCA模型下得到的马氏距离值最小，就将此样本判为哪一类。

上述方法中，步骤(4.3)中，样本i到步骤(3.1)中所建PCA模型的中心(O＝{0,0})的马氏距离Dij的计算公式如下：

上述方法中，利用得分向量计算验证集Smv中样本i的T_i²，T_i²计算公式如下：

然后用F检验计算T²的临界值

公式(4)中自由度分别为A和(n-A)，n为建模的样本数，A为确定的最佳主成分数。

上述方法中，PCA模型的残差阈值Q，可以用建模样本集的二次分布结果来近似确定，残差阈值Q计算公式如下：

其中，z_α为置信上限为100(1-α)％时的单位偏差，α的置信区间为0.04～0.06；

其中，m为样本属性的维度，λ_j是协方差矩阵第j个特征值；

此时，可将和作为样本的属性，于是可将样本表示为Z＝{x_i|i＝1,2……m}，其中

上述方法适用于对固体、液体、气体状态的多组分样品的识别。在对固体状态的多组分样品识别时，制备样本时，需要将固体样本摊开使得厚度均匀；而在对液体状态的多组分样品识别时，制备样本时，需要将液体样本充分静置使得密度均匀；在对气体状态的多组分样品识别时，制备样本时，可将气体状态的多组分样品直接充入已预先抽真空的气体池制备成待监测样本。

本发明具有如下有益效果：

本发明提出了一种新的光谱多元分析分类与识别方法，针对SIMCA方法区分成分相近又存在着微小差异的样本时精度不够的问题，分析了是因为SICMA采用了欧氏距离来预测样本的类别。而大多的情况下，样本分布空间具有一定的方向性和不规则性，通常不符合欧氏距离的分布。马氏距离引进(或除以)了协方差，考虑了数据属性的相关性，排除变量之间的干扰，在一定程度上凸显了表达能力强的属性。因此，本发明采用了马氏距离代替欧氏距离来预测样本的类别，改善SICMA方法的分类精度。

本发明可适用于固体、液体、气体状态的多组分样品，例如石油类产品(如汽油，柴油等)、农产品(如粮食、茶、棉、麻、烟叶、果蔬等)、食品(如饲料、肉类、酒等)、医药等样品的识别。具有应用范围广，精度高的特点。

附图说明

图1是使用马氏距离和欧氏距离计算的样品分布范围。

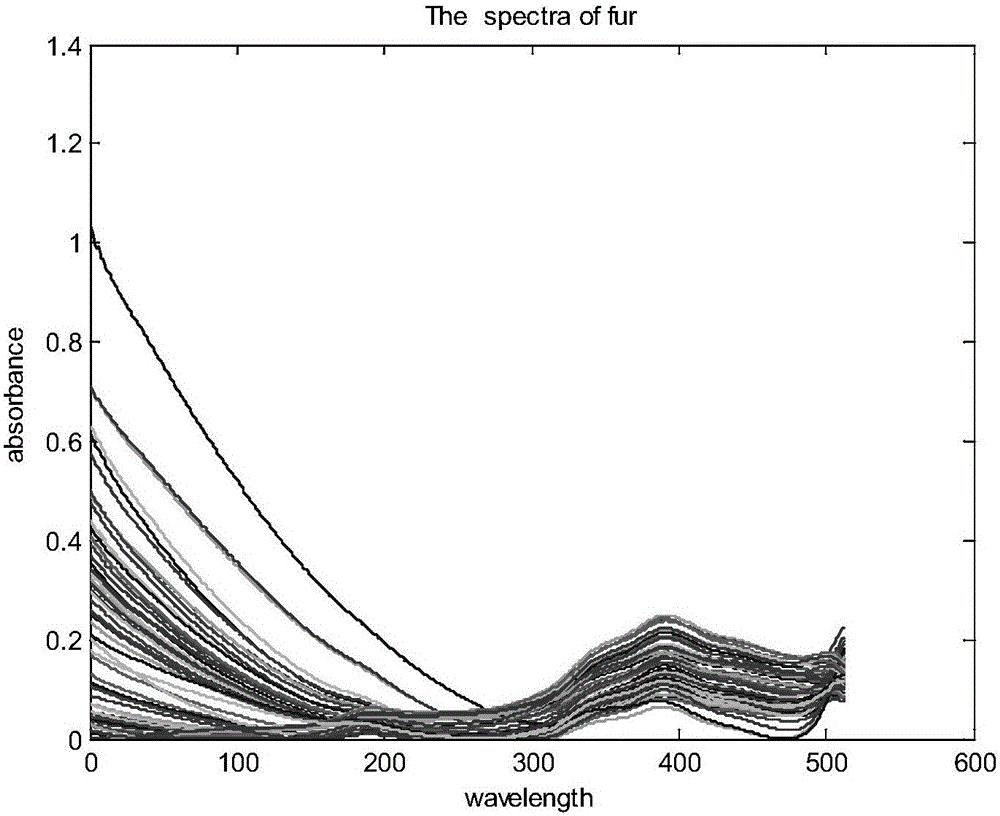
图2是实例1中采集的原始光谱图。

图3是实例1中各个类的PRESS图和相应的T²和Q分布图。

图4是实例2中采集的原始光谱图。

图5是实例2中各个类的PRESS图和相应的T²和Q分布图。

具体实施方式

下面结合附图对本发明作进一步描述。本发明实例用来解释本发明，而不是对本发明进行限制，在本发明的精神和权利要求的保护范围内，对本发明做出的任何修改和改变，都落入本发明的保护范围。

实施例1

本实施案例分别为貉子，狐狸和兔子的皮毛，共76组样本，由北京市毛麻丝织品质量监督检验站提供。采用HF-P12型纺织品成分分析仪(西派特(北京)科技有限公司产品)采集样品的漫反射近红外光谱，光谱范围为900-1700nm，分辨率为3.1nm，积分时间100ms。以聚四氟参考板采集参比信号。将皮毛样本平铺在分析仪采样平台上，样本用金属砝码压平压实，对每个样品采集3张漫反射近红外光谱谱图，取其平均光谱为样本光谱。图1为皮毛样本的原始光谱图。

本实例实施的主要步骤如下：

1.对光谱数据采用SG平滑方法消除数据中高频噪音，用一阶求导方法消除基线漂移，然后对此光谱数据进行均值中心化处理。

2.对皮毛样本数据集随机划分为校正集Smc和验证集Smv，其中，校正集Smc和验证集Smv分别占总样本数的80％和20％。

3.对校正集Smc中的每类样本建立主成分模型，用交叉验证计算预测误差平方加和PRESS，根据PRESS随主成分数变化曲线确定模型的最佳主成分数A。并根据Hotelling T2检验计算T²临界值根据建模样本集的二次分布结果近似出残差阈值Q。图2为样本各个类的PRESS图和相应的T²和残差分布图。参考图2,3类模型的主因子数分别确定为8，4和8。

4.根据主成分模型的最佳主成分数A计算验证集Smv中样本的T²和残差S_i的值，利用T²的临界值和残差阈值Q，对验证集Smv中的样本i进行特征提取，于是样本i可表示为

5.分别计算每一类PCA模型下样品到模型中心(O＝{0,0})的欧氏距离。根据最小的Di值，判别待测样本的类别。

6.分别计算每一类PCA模型下样品到模型中心(O＝{0,0})的马氏距离。根据最小的Di值，判别待测样本的类别。

7.根据预测结果的准确率，评价马氏距离和欧氏距离的分类效果。

表1为马氏距离和马氏距离对皮毛样本的分类结果对比，由表中结果可知，用马氏距离预测验证集Smv类别的准确率明显大于欧氏距离的。表明马氏距离具有更强的分类与识别能力。

表1皮毛样本分类结果对比

实施例2

食用油样本为从北京市场上采购的橄榄油和芝麻油，模拟食用油掺假。取5ml橄榄油,分别加入不同体积的芝麻油，将样本用振荡器摇晃均匀，放置稳定一段时间，制备橄榄油/芝麻油比例为1％～8％的调和油，共104个样本。将1％～4％比例范围的调和油划为第一类，5％～8％比例范围的调和油划为第二类。采用带有ATR晶体的Agilent5500型红外光谱仪测量样本的红外光谱。光谱范围为650-4000cm^-1，分辨率为4cm^-1,扫描次数为32。以空气为参比，用滴管吸入少量样本滴在ATR晶体表面上，每个样品采集3张红外谱图，取其平均光谱作为样本光谱。然后使用酒精溶剂清洗ATR晶体至无样本污染后，再采集下一个样本的光谱。图3为食用油的原始光谱图。

本实例实施的主要步骤如下：

1.对光谱数据采用SG平滑方法消除数据中高频噪音，用一阶求导方法消除基线漂移，然后对此光谱数据进行均值中心化处理。

2.对于2类食用油样本数据集，在3％～6％比例范围内随机选出20组样本作为验证集Smv，其余样本作为校正集Smc。校正集Smc占总样本数的80％。

3.对校正集Smc中的每类样本建立主成分模型，用交叉验证计算预测误差平方加和(PRESS)，根据PRESS随主成分数变化曲线确定模型的最佳主成分数A。并根据Hotelling T2检验计算T²临界值根据建模样本集的二次分布结果近似出残差阈值Q。图4为样本各个类的PRESS图和相应的T²和残差分布图。参考图4,2类模型的主因子数分别确定为14和13。

4.根据主成分模型的最佳主成分数A计算验证集Smv中样本的T²和残差S_i的值，利用T²的临界值和残差阈值Q，对验证集Smv中的样本i进行特征提取，于是样本i可表示为

5.分别计算每一类PCA模型下样品到模型中心(O＝{0,0})的欧氏距离。根据最小的Di值，判别待测样本的类别。

6.分别计算每一类PCA模型下样品到模型中心(O＝{0,0})的马氏距离。根据最小的Di值，判别待测样本的类别。

7.根据预测结果的准确率，评价马氏距离和欧氏距离的分类效果。

表2为马氏距离和马氏距离对食用油样本的分类结果对比，从图4可以看出，2类的样本基本分开，部分不同类样本还是很接近的。说明不同类的调和油之间差别较小，分类有较大难度。由表2的分类结果可知，马氏距离和欧氏距离都不能将样本全部识别出来。但是，与欧氏距离相比，的分类结果明显改善。同样的样本模型，欧氏距离的分类准确率为60％，而马氏距离的准确率上升到了70％，因此马氏距离的分类与识别能力更优。

表2食用油分类结果的对比