声矢量传感器阵列空间旋转解相干到达角估计方法与流程

本发明属于信号处理技术领域，尤其涉及一种声矢量传感器阵列的相干源到达角估计方法。

背景技术：

在实际中由于信号传输过程的多径现象和回波信号以及人为干扰，使得相关信号源非常普遍，所以基于相关源的检测和估计是信号处理的重要研究课题。当入射信号相互独立时子空间类方法有很好的参数估计性能，但是如果入射的信号是相干信号以music为代表的子空间类算法将失效。当入射信号是相干信号时，信号子空间的维数将小于信号源个数，信号子空间扩散到了噪声子空间，从而导致信号子空间和噪声子空间不完全垂直，从而导致子空间类算法失效，无法进行方向估计。

为使相干信源doa估计中的上述难题得到有效的解决，国内外学者提出了一系列的解相干方法，这些方法的关键是如何恢复信号协方差矩阵的秩。目前解相干的方法大致可以分为两类，一类是以空间平滑和矩阵重构法为代表的降维方法，一类是以聚焦和虚拟变换法为代表的非降维方法，这些方法解决了信号相关问题但仍有一定的局限性和不足，以聚焦处理为代表的非降维算法的计算复杂度高；以空间平滑为代表的降维方法减小了阵列孔径，增大了阵列的波束宽度，降低了参数估计精度。且空间平滑一般只适用于均匀阵，严重限制了方法的应用范围。声矢量传感器是一种新型的声源信号测向设备，它是由三个相互正交的质点振速传感器和一个声压传感器构成，因而能够空间共点同步测量声场中某处的声压强度和质点振速。声矢量传感器阵列与标量传感器阵列相比较，声矢量传感器阵列不仅能够获取阵列孔径信息，而且蕴含矢量传感器各分量之间的正交信息，因而具有更高的空间分辨力和测向精度，近年来已成为国内外学者研究的热点问题。本发明针对现有方法的不足利用声矢量传感器阵列自身的矢量结构特性，将声矢量传感器阵列分成声压子阵、x轴振速子阵、y轴振速子阵和z轴振速子阵四个子阵，根据子阵的旋转不变特性解相干，该方法适用于均匀和非均匀声矢量传感器线阵。

技术实现要素：

本发明的目的是提供一种远场窄带相干源声矢量传感器阵列解相干到达角估计方法。

为了实现上述目的，本发明采取如下的技术解决方案：

声矢量传感器阵列空间旋转解相干到达角估计方法，k个相干窄带、平稳远场声源信号从不同的方向θk入射到该接收阵列上，θk∈[0，π/2]是第k个信号的俯仰角，k＝1，…，k，所述阵列由m个在x轴上任意分布的声矢量传感器阵元构成，所述阵元是具有空间共点同步测量声压以及x轴、y轴和z轴方向振速分量的声矢量传感器，所有传感器的对应通道相互平行：所有的声压传感器相互平行，所有的x轴方向振速传感器相互平行，所有的y轴方向振速传感器相互平行，以及所有的z轴方向振速传感器相互平行；任意两个相邻阵元间距小于等于λmin/2，λmin为入射声波信号的最小波长；

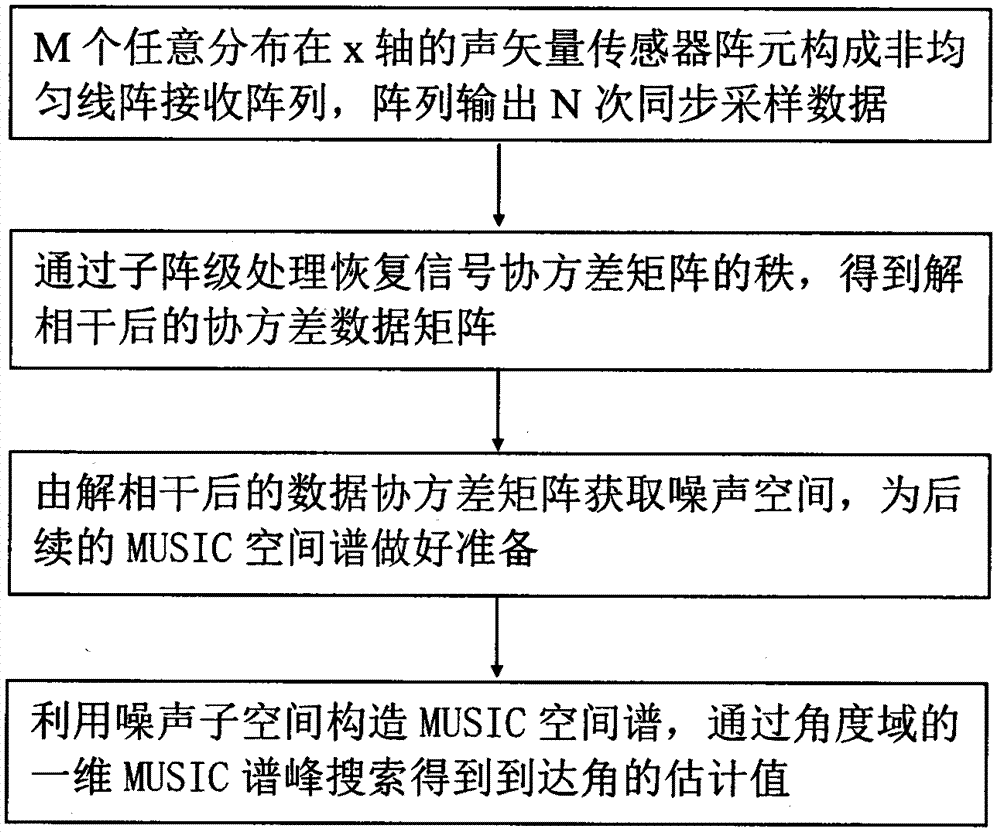
声矢量传感器阵列空间旋转解相干到达角估计方法步骤如下：

步骤一、m个任意分布在x轴的声矢量传感器阵元构成非均匀线阵接收阵列，阵列输出n次同步采样数据z；

步骤二、通过子阵级处理恢复信号协方差矩阵的秩，得到解相干后的协方差数据矩阵rz；

根据阵列数据z的排布规律将数据分成声压以及x轴、y轴和z轴方向振速子阵数据，计算四个子阵数据的协方差矩阵和其中，和分别是声压以及x轴、y轴和z轴方向振速子阵数据协方差矩阵，通过四个子阵数据协方差矩阵的算术平均得到解相干后的满秩数据协方差矩阵rz；

步骤三、由解相干后的数据协方差矩阵rz获取噪声空间；

通过对数据协方差矩阵rz进行特征分解，k个大特征对应的特征矢量构成信号子空间us，m-k个小特征值对应的特征矢量构成噪声子空间un；

步骤四、利用噪声子空间un构造music空间谱通过角度域θ∈[0，π/2]的一维music谱峰搜索得到到达角的估计值

本发明采用的x轴上任意分布的线阵，阵列的阵元为由声压传感器和x轴、y轴及z轴方向的振速传感器构成的声矢量传感器，并且所有的声压传感器相互平行，所有的x轴方向振速传感器相互平行，所有的y轴方向振速传感器相互平行，所有的z轴方向振速传感器相互平行。本发明利用声矢量传感器自身具有的正交矢量特性，给出了声矢量传感器空间旋转解相干方法，本发明方法没有减小阵列孔径信息，具有更高的空间分辨力和测向精度，打破了原有空间平滑方法仅适用于均匀阵列的限制，扩大了方法的适用范围。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中需要使用的附图做简单介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明实施例声矢量传感器阵列的示意图；

图2为本发明方法的流程图；

图3为信噪比是0db时三种方法在均匀线阵条件下到达角估计性能比较；

图4为信噪比是2db时三种方法在均匀线阵条件下到达角估计性能比较；

图5为信噪比是4db时三种方法在均匀线阵条件下到达角估计性能比较；

图6为信噪比是0db时三种方法在非均匀线阵条件下到达角估计性能比较；

图7为信噪比是2db时三种方法在非均匀线阵条件下到达角估计性能比较；

图8为信噪比是4db时三种方法在非均匀线阵条件下到达角估计性能比较；

具体实施方式

为了让本发明的上述和其它目的、特征及优点能更明显，下文特举本发明实施例，并配合所附图示，做详细说明如下。

图1所示为本发明实施例的声矢量传感器阵列的示意图。本发明的声矢量传感器阵列由m个x轴上任意分布的阵元构成，所述阵元是具有空间共点同步测量声压以及x轴、y轴和z轴方向振速分量的声矢量传感器；任意两个相邻阵元间距小于等于λmin/2，λmin为入射声波信号的最小波长；

参照图2，本发明的解相干到达角估计方法的步骤如下：x轴上任意分布声矢量传感器线阵接收k个相干窄带、平稳远场声源信号，k为入射声源信号的数量，

步骤一、m个任意分布在x轴的声矢量传感器阵元构成非均匀线阵接收阵列，阵列输出n次同步采样数据z；

步骤二、通过子阵级处理恢复信号协方差矩阵的秩，得到解相干后的协方差数据矩阵rz；

根据阵列数据z的排布规律将数据分成声压以及x轴、y轴和z轴方向振速子阵数据，计算四个子阵数据的协方差矩阵和其中，和分别是声压以及x轴、y轴和z轴方向振速子阵数据协方差矩阵，通过四个子阵数据协方差矩阵的算术平均得到解相干后的满秩数据协方差矩阵rz；

步骤三、由解相干后的数据协方差矩阵rz获取噪声空间；

通过对数据协方差矩阵rz进行特征分解，k个大特征对应的特征矢量构成信号子空间us，m-k个小特征值对应的特征矢量构成噪声子空间un；

步骤四、利用噪声子空间un构造music空间谱通过角度域θ∈[0，π/2]的一维music谱峰搜索得到到达角的估计值

本发明给出了x轴上任意分布声矢量传感器线阵解相干到达角估计方法，充分利用声矢量传感器阵列自身的矢量结构特性进行解相干处理，将声矢量传感器阵列分成声压子阵、x轴振速子阵、y轴振速子阵和z轴振速子阵四个子阵，然后通过子阵数据协方差矩阵算术平均解相干，然后利用子空间方法得到噪声子空间，构造music谱，通过一维角度搜索完成到达角的估计。相比于解相干前的传统music方法和空间平滑解相干方法，本发明方法突破了现有空间平滑解相干只适用于均匀阵局限，对于均匀线阵和非均匀线阵均成立，且不损失阵列孔径，相同条件下参数估计精度高于空间平滑方法。

本发明的效果可以通过以下的仿真结果进一步说明：

仿真实验1：

仿真实验条件如下：两个相干窄带、平稳远场声源信号入射到由8个在x轴上均匀分布的声矢量传感器阵元构成的线性阵列，如图1所示，阵元间隔等于0.5λmin，入射信号的参数为：(θ1，θ2)＝(15°，50°)，快拍数为512次；

仿真实验结果如图3至图5所示，图3-5为信噪比分别是0db、2db和4db、时，x轴上均匀线阵下的解相干前传统music方法、空间平滑解相干方法和本发明方法的到达角估计结果，从图3-5可以看出在同样信噪比条件下，空间平滑解相干方法和本发明方法都能解相干，但相比于空间平滑解相干方法，本发明方法的空间谱更尖锐，有更高的到达角参数估计精度。

仿真实验2：

仿真实验条件如下：该仿真实验的两个相干窄带、平稳远场声源信号入射到由8个在x轴上任意分布的声矢量传感器阵元构成的非均匀线阵，阵元间隔小于等于0.5λmin且随机分布，入射信号的参数为：(θ1，θ2)＝(15°，50°)，快拍数为512次。

仿真实验结果如图6至图8所示，图6-8为信噪比分别是0、2db和4db时，x轴上非均匀线阵下的解相干前传统music方法、空间平滑解相干方法和本发明方法到达角空间谱估计结果，从图6-8可以看出在同样信噪比条件下，在非均匀线阵下空间平滑解相干方法没有形成谱峰，空间平滑解相干方法失效，而本发明方法能够形成尖锐谱峰，从而说明本发明方法对非均匀线阵也适用，从而验证了本发明方法的正确性。

以上所述，仅是本发明的较佳实施例而已，并非对本发明做任何形式上的限制，虽然本发明已以较佳实施例揭露如上，然而并非用以限定本发明，任何熟悉本专业的技术人员，在不脱离本发明技术方案范围内，当可利用上述揭示的技术内容做出些许更动或修饰为等同变化的等效实施例，但凡是未脱离本发明技术方案的内容，依据本发明的技术实质对以上实施例所作的任何简单修改、等同变化与修饰，均仍属于本发明技术方案的范围内。