一种基于压缩感知的自由度增加型互质阵列波达方向估计方法与流程

本发明属于信号处理技术领域，尤其涉及对雷达信号、声学信号及电磁信号的波达方向估计，具体是一种基于互质阵列接收信号压缩感知的自由度增加型波达方向估计方法，可用于无源定位和目标探测。

背景技术：

波达方向(direction-of-arrival,doa)估计是阵列信号处理领域的一个重要分支，它是指利用阵列天线接收空域信号，并通过现代信号处理技术和各类优化方法实现对接收信号统计量进行有效处理，以实现信号的doa估计，在雷达、声呐、语音、无线通信等领域有着重要的应用价值。

doa估计方法的自由度是指其能够同时分辨的入射信号源的个数，作为实际系统应用中的一个重要衡量指标，决定着系统的总体复杂度。现有的doa估计方法通常采用均匀线性阵列进行信号的接收与建模，但是基于均匀线性阵列方法的自由度是受实际天线阵元个数限制的。具体而言，对于一个包含l个天线阵元的均匀线性阵列，其自由度为l-1。因此，当某个空域范围内入射信号源的个数大于阵列中天线阵元的个数时，现有采用均匀线性阵列的方法将无法进行有效的doa估计。为了增加自由度，传统方法需要通过增加物理天线阵元的个数来实现，这造成了系统计算复杂度和硬件复杂度的增加。因此，现有doa估计方法在自由度性能与计算复杂度之间存在着一定的利弊权衡问题。

互质阵列能够在天线阵元个数一定的前提下增加doa估计的自由度，因而受到了学术界的广泛关注。作为互质采样技术在空间域上的一个典型表现形式，互质阵列提供了一个系统性的稀疏阵列架构方案，并能够突破传统均匀线性阵列自由度受限的瓶颈，实现doa估计方法自由度性能的提升。现有的基于互质阵列的doa估计方法主要通过利用质数的性质将互质阵列推导到虚拟域，并形成等价虚拟均匀线性阵列接收信号以实现doa估计。由于虚拟阵列中包含的虚拟阵元数大于实际的天线阵元数，自由度因此得到了有效的提升。但是，现有基于等价虚拟信号的doa估计方法计算复杂度较高，在实际应用中，我们希望用较低的计算复杂度实现自由度的提升。

技术实现要素：

本发明的目的在于针对上述现有技术存在的不足，提出一种基于压缩感知的自由度增加型互质阵列波达方向估计方法，在降低计算复杂度的同时，充分利用互质阵列的特性以增加doa估计的自由度，从而有效降低在实际系统应用过程中的计算复杂度与硬件复杂度，提高系统的整体效率。

本发明的目的是通过以下技术方案来实现的：一种基于压缩感知的自由度增加型互质阵列波达方向估计方法，该方法包含以下步骤：

(1)接收端使用m+n-1个天线，并按照互质阵列结构进行架构；其中m与n为互质整数；

(2)利用互质阵列接收d个方向为θ1，θ2,…,θd的远场窄带非相干信号源的入射信号，得到(m+n-1)×1维互质阵列接收信号x(k)，共采集k个采样快拍得到x＝[x(1),x(2),…,x(k)]；

(3)构造一个压缩感知核φ：φ是一个q×(m+n-1)维矩阵；其中q为压缩系数，满足q<<m+n-1且q>d；φ中的元素随机生成，且满足行正交的条件；

(4)利用压缩感知核将(m+n-1)×1维互质阵列接收信号x(k)以随机投影的方式压缩为q×1维轮廓信号y(k)，即y(k)＝φx(k)；对于k个采样快拍得到y＝[y(1),y(2),…,y(k)]；

(5)根据k个采样的轮廓信号计算q×q维轮廓信号采样协方差矩阵

(6)通过向量化轮廓信号的采样协方差矩阵计算轮廓信号所对应的等价虚拟信号z：

其中，为q²×d维压缩后的虚拟阵列导引矩阵，

这里，vec(·)表示向量化操作，即将矩阵中的各列按序堆叠成一个新的向量，(·)^*和(·)^t分别表示共轭和转置操作，表示克罗内克积，d＝1,2,…，d,为d个入射信号的功率，为噪声功率，im+n-1为(m+n-1)×(m+n-1)维单位矩阵，互质阵列导引向量a(θd)可表示为：

其中ui,i＝1,2,…,m+n-1为互质阵列的天线阵元位置，λ为入射信号的波长；

(7)构造虚拟域稀疏信号重建优化问题并求解。首先根据空间域信号的稀疏特性，将波达方向角的角度域范围等间距划分成个网格点，即然后根据等价虚拟信号z构建如下以为变量的虚拟域稀疏信号重建优化问题：

其中为维矩阵，且包含个方向上信号的功率信息，∈为阈值常数，用于约束信号重建的误差。将上述非凸优化问题转化成凸优化问题，并求解得到最优解

(8)通过谱峰搜索的方式，寻找维空间谱的峰值，并将其包含的重建信号功率值从大到小排列，前d个峰值所对应的x轴角度方向即为波达方向估计结果。

进一步地，步骤(1)所述的互质阵列具体结构为：互质阵列由一对稀疏均匀线性子阵列组合而成，第一个子阵列包含m个天线阵元，且阵元间距为nd；第二个子阵列包含n个天线阵元，且阵元间距为md；d为入射窄带信号波长λ的一半。将两个子阵列以首个天线阵元重叠的方式进行组合，得到包含m+n-1个天线阵元的互质阵列结构。

进一步地，步骤(5)所述的轮廓信号采样协方差矩阵计算方法为：

也可以通过以下计算方法等价得到：

其中为互质阵列接收信号的采样协方差矩阵，可表示为：

进一步地，步骤(6)所述的虚拟信号z可等价表示为：

其中，为(m+n-1)²×d维虚拟阵列导引矩阵，i＝vec(im+n-1)。

进一步地，步骤(7)中，将虚拟域稀疏信号重建非凸优化问题，引入1范数松弛技术，转化为如下凸优化问题：

进一步地，步骤(7)中，将虚拟域稀疏信号重建非凸优化问题转化为如下基追踪去噪优化问题：

其中，ξ为正则化参数，用于权衡虚拟域信号重建误差和空间谱的稀疏性。

本发明与现有技术相比具有以下优点：

(1)本发明充分利用了互质阵列能够增加doa估计的自由度这一优势，将获得的轮廓信号协方差矩阵推导至虚拟域，并通过虚拟域稀疏信号重建实现doa估计，可分辨的入射信号源个数大于物理天线阵元个数；

(2)本发明引入了压缩感知的思想，通过压缩感知核的设计将互质阵列接收信号压缩为轮廓信号，原始接收信号中包含的核心信息在轮廓信号中得以保留，从而可以直接利用轮廓信号实现自由度增加型的doa估计；与此同时，压缩感知核行正交的结构设计有效地避免了加性高斯噪声对于轮廓信号采样协方差矩阵计算的影响；

(3)本发明利用q²×1维由轮廓信号推导而来的等价虚拟信号进行虚拟域稀疏信号重建优化问题设计；与直接采用(m+n-1)²×1维由互质阵列接收信号推导而来的虚拟信号稀疏重建方法相比，有效地降低了计算复杂度。

附图说明

图1是本发明的方法总体流程框图。

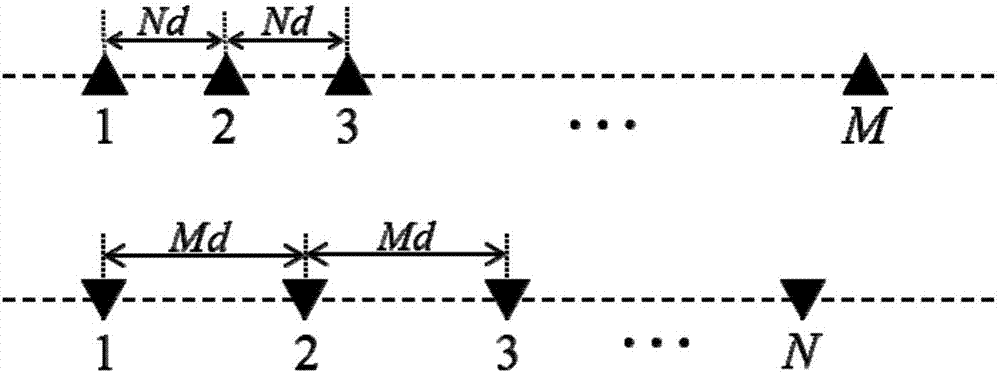
图2是本发明中组成互质阵列的一对稀疏均匀子阵列结构示意图。

图3是本发明中互质阵列的结构示意图。

图4是本发明所提方法与现有各方法的空间谱对比示意图；其中图4(a)是互质阵列多重信号子空间分类方法；图4(b)是互质阵列等价虚拟信号协方差矩阵稀疏重建方法；图4(c)是采用互质阵列接收信号的虚拟信号稀疏重建方法；图4(d)是本发明所提方法。

具体实施方式

以下参照附图，对本发明的技术方案和效果作进一步的详细说明。

对于doa估计方法在实际系统中的应用，较高的自由度与较低的计算复杂度是两个期望的技术性能特征。但是受限于天线阵列结构、阵元个数等因素，现有方法在这两项性能上无法同时实现优化，往往存在着利弊权衡问题。为了在较低的计算复杂度条件下实现doa估计方法自由度的增加，本发明提供了一种基于压缩感知的自由度增加型互质阵列波达方向估计方法，参照图1，本发明的实现步骤如下：

步骤一：在接收端使用m+n-1个天线阵元架构互质阵列；首先，选取一组互质整数m、n；然后，参照图2，构造一对稀疏均匀线性子阵列，其中第一个子阵列包含m个间距为nd的天线阵元，其位置为0,nd,…,(m-1)nd；而第二个子阵列包含n个间距为md的天线阵元，其位置为0,md,…,(n-1)md；单位间隔d取为入射窄带信号波长的一半，即d＝λ/2；接着，将两个子阵列的首个天线阵元视为参考阵元，参照图3，将两个子阵的参考阵元重叠以实现子阵列组合，获得实际包含m+n-1个天线阵元的非均匀互质阵列架构。

步骤二：利用互质阵列接收入射信号并建模；假设存在d个远场窄带非相干信号源，采用步骤一架构的非均匀互质阵列接收入射信号，得到(m+n-1)×1维互质阵列接收信号x(k)；共采集k个采样快拍，得到接收信号矩阵为x＝[x(1),x(2),…,x(k)]。

步骤三：构造一个压缩感知核φ；该压缩感知核φ是一个q×(m+n-1)维矩阵；其中q为压缩系数，满足q<<m+n-1且q>d；压缩感知核中的元素随机生成，如满足高斯分布、伯努利分布等随机分布条件；压缩感知核中的元素需满足行正交的条件，即φφ^h＝iq，其中iq为q×q维单位矩阵。

步骤四：利用步骤三所生成的压缩感知核φ将步骤二所得的(m+n-1)×1维互质阵列接收信号x(k)进行压缩，得到q×1维轮廓信号y(k)；压缩的方式为随机投影；对每一个采样快拍，通过以下公式实现：

y(k)＝φx(k)。

步骤五：根据k个采样快拍所获得的轮廓信号y＝[y(1),y(2),…,y(k)]计算q×q维轮廓信号采样协方差矩阵可表示为：

其中(·)^h表示共轭转置操作；由于压缩感知核φ满足行正交的条件，轮廓信号的采样协方差矩阵也可以通过以下计算方法等价得到：

其中为互质阵列接收信号的采样协方差矩阵，可表示为：

步骤六：通过向量化轮廓信号的采样协方差矩阵计算轮廓信号所对应的等价虚拟阵列接收信号z：

其中，为(m+n-1)²×d维虚拟阵列导引矩阵，i＝vec(im+n-1)。这里，vec(·)表示向量化操作，即将矩阵中的各列按序堆叠成一个新的向量，(·)^*和(·)^t分别表示共轭和转置操作，表示克罗内克积，d＝1,2,…,d,为d个入射信号的功率，为噪声功率，互质阵列导引向量a(θd)可表示为：

其中ui,i＝1,2,…,m+n-1为互质阵列的天线阵元位置。根据以下关系：

轮廓信号所对应的等价虚拟阵列接收信号z可进一步表示为：

其中，为q²×d维压缩后的虚拟阵列导引矩阵，向量z可视作虚拟阵列所接收到的等价虚拟信号，其相应的虚拟阵列导引矩阵为

步骤七：构造虚拟域稀疏信号重建优化问题并求解。首先根据空间域信号的稀疏特性，将波达方向角的角度域范围等间距划分成个网格点，即然后根据由步骤六计算得到的等价虚拟信号z构建如下以为变量的优化问题：

其中，为维矩阵，且包含个方向上信号的功率信息，∈为阈值常数，用于约束信号重建的误差，‖·‖0和‖·‖2分别表示0范数和2范数。由于上述优化问题属于非凸问题，这将导致求解困难；为了获得优化解我们考虑将优化问题中的0范数替换为1范数，进而实现凸松弛，得到以下凸优化问题：

其中‖·‖1表示1范数。上述凸优化问题可等价写为一个基追踪去噪优化问题：

其中ξ为正则化参数，用于权衡信号重建误差和空间谱的稀疏性。求解上述凸优化问题可得到最优化值

步骤八：通过谱峰搜索寻找空间谱的峰值，并将其包含的重建信号功率值从大到小排列，前d个峰值所对应的x轴角度方向即为波达方向估计结果。

本发明一方面充分利用了互质阵列能够增加doa估计方法自由度的优势，突破了均匀线性阵列自由度受限的瓶颈，实现了在天线阵元个数一定的条件下估计更多个数的入射信号源；另一方面引入了压缩感知的思想，通过压缩感知核的设计将(m+n-1)×1维互质阵列接收信号压缩为q×1维轮廓信号，原始接收信号中包含的核心信息在轮廓信号中得以保留，有效地降低了稀疏信号重建优化问题的计算复杂度。

下面结合仿真实例对本发明的效果做进一步的描述。

仿真条件：互质阵列的参数选取为m＝5，n＝6，即架构的互质阵列共包含m+n-1＝10个天线阵元。假定入射窄带信号个数为16，且入射方向均匀分布于-60°至60°这一区间范围内；压缩系数q设置为8，压缩感知核φ中的元素满足独立同分布的随机高斯分布，均值为0，方差为1/(m+n-1)；波达方向角的角度域范围为[-90°,90°]，空间域网格点均匀采样间距设置为0.1°；正则化参数ξ设置为0.25；信噪比设置为10db，采样快拍数k＝500。

仿真实例：本发明所提出的采用互质阵列轮廓信号的自由度增加型doa估计方法将与现有的互质阵列多重信号子空间分类方法、互质阵列等价虚拟信号协方差矩阵稀疏重建方法、采用互质阵列接收信号的虚拟信号稀疏重建方法进行比较，以说明本发明方法在自由度和计算复杂度方面的优势。由于仿真条件中入射信号源的个数大于天线阵元的个数，采用均匀线性阵列的方法自由度受限而无法实现有效的doa估计，因而在此不作比较。

各方法的归一化空间谱如图4所示，其中，虚线表示真实的入射信号波达方向。可以看出，互质阵列多重信号子空间分类方法和互质阵列等价虚拟信号协方差矩阵稀疏重建方法未能实现所有入射信号源的有效分辨，这是因为这两种方法均包含空间平滑的步骤；由于空间平滑需要一个连续的虚拟阵列以实现有效的信号处理，自由度在一定程度上受到了限制，在该仿真条件下最高可达到的自由度仅为10。相比之下，本发明所提方法与采用互质阵列接收信号的虚拟信号稀疏重建方法均能够利用10个物理天线阵元实现16个信号源的有效估计，说明了doa估计方法的自由度得到了提升。但是，本发明所提方法采用由轮廓信号所推导而来的等价虚拟信号实现稀疏信号重建，其维度为q²×1维，而利用互质阵列接收信号的虚拟信号稀疏重建方法则采用(m+n-1)²×1维等价虚拟信号进行重建，且两者的归一化空间谱性能类似，这说明了本发明所提方法的计算复杂度得到了极大地降低。因此，仿真实例对比表明本发明所提方法能够在降低计算复杂度的同时提升doa估计方法的自由度。

综上所述，本发明主要解决了现有技术在doa估计自由度性能与计算复杂度方面存在的不足，一方面充分利用互质阵列的特性在虚拟域进行信号处理以实现自由度的增加；另一方面引入压缩感知的方法有效地降低了计算复杂度，在无源定位和目标探测等实际应用中表现出突出的优势。