一种结合IMU和导航影像的月面巡视器快速定位方法与流程

本发明属于深空探测技术领域，具体涉及一种结合IMU和导航影像的月面巡视器快速定位方法。

背景技术：

巡视器的高精度导航定位技术是深空探测领域中的关键技术之一，高精度的定位结果不仅可以确保巡视器的安全，而且可以使巡视器与地面控制系统通信时具有较好的指向角度，进而为实现资源勘查等科学考察任务提供基础。目前，月面巡视器的导航定位方法主要分为三类，包括：基于VLBI的定位方法、基于里程计和IMU结合的定位方法和基于摄影测量的定位方法。

(1)基于VLBI的定位方法研究现状：

刘庆会等(2010)提出了超高精度多频点同波束VLBI技术的月球车精密相对定位方法，在得到误差10m的着陆区月面地形图后，利用多频点同波束VLBI差分相位时延和测距数据,有望实现误差10m的月球车在月面上的相对定位。魏二虎等(2016)提出了联合VLBI和天文导航的月球车定位方法，定位结果在纬度方向误差范围在-33至31m，经度方向误差范围在5.5至6.5m。上述定位结果的精度无法满足巡视器科学考察的需求。

童锋贤等(2014)先将探月VLBI结果转为通用FITS-IDI格式，然后对着陆器和巡视器进行相位参考成像，得到巡视器天线相对于着陆器天线的位置，相对定位精度约1m。但是该方法的定位过程中需要用到巡视器和着陆器天线的相对高度差，而该高度差无法精确获取，因此，其定位结果需要借助其他手段获取该值，当高度差无法精确获取时，定位结果的精度会大幅度降低。

李培佳等(2014)利用同波束VLBI数据进行月面巡视器与着陆器的相对定位，标称精度优于1m。黄勇等(2014)采用VLBI差分相时延计算得到巡视器相对于着陆器的相对位置，误差在1m左右。昌胜骐等(2015)提出利用搜索法对巡视器和着陆器的相对位置进行确定，并与统计定位结果比较，位置差小于1m。周欢等(2015)提出了采用天文同波束相位参考成图技术进行深空探测器相对定位的方法，巡视器相对着陆器定位精度达到米级。郭丽等(2016)采用中国VLBI网的同波束技术对嫦娥三号巡视器进行了跟踪测量，获得了1M的相对定位精度。

(2)基于IMU结合里程计定位方法研究现状：

夏凌楠等(2013)提出结合惯性传感器和视觉里程计的定位算法，以扩展卡尔曼滤波(extended Kalman filter，EKF)为框架，利用惯性传感器的航位推算构建EKF的过程模型，视觉里程计作为相对线速度和相对角速度传感器用来建模观测方程，优化了定位结果。但是上述方法并没有针对月面重力仅为地球1/6的情况下的车轮打滑导致里程计观测出现较大误差的情况开展研究。李宇等(2015)提出了一种基于联邦滤波的IMU/里程仪组合导航方法，提高了组合导航定位系统精度和稳健性。但是其实验仅仅是在地球上做了测试，并没有采用真实的嫦娥三号的实验数据进行测试。因此，其对巡视器定位的适用性有待商榷。刘传凯等(2014)提出了惯导与视觉组合定姿定位方法，但是该方法并没有真正意义上的实现惯导与摄影测量方法的组合，而是仅仅将惯导参数作为光束法迭代计算的初值，当月面特征点较少时，无法完成定位。

(3)基于摄影测量的巡视器定位方法研究现状：

基于摄影测量手段的巡视器定位方法在国内开展的比较多。邸凯昌等2015提出了一种基于连续图像序列的光束法平差定位方法。李琳辉等(2011)针对沙质的月面模拟环境提出了对极线约束下的角点的匹配，并且通过优化搜索窗口尺寸和预估搜索方向等方法提高匹配和跟踪的效率。王保丰等(2014)将SIFT匹配、相关系数匹配、最小二乘匹配和光束法平差等多项技术融合，实现了相邻站间月面巡视器的导航定位。徐辛超等(2015)提出了基于空间后方交会迭代法的巡视器单摄站定位方法，但需要至少3个以上的控制点才能完成解算。马友青等，提出一种利用列文伯格－马夸尔特算法(LM算法)代替高斯牛顿算法，进行图像光束法平差的巡视器导航定位方法，提高了迭代过程的收敛速率。刘召芹等(2014)通过对导航相机原始影像进行匹配定位实现月球车的连续定位，并利用导航相机生成的DOM与CE-2DOM进行特征匹配，根据匹配的结果实现月球车在CE-2卫星影像上的定位。刘少创等(2015)在地面控制场中,采用基于控制点的光束法平差方法获得精确的相机标定参数，然后通过像点匹配、前方交会完成图像的立体模型构建，并根据不同摄站间的连接点序列建立立体图像条带网，最终对立体图像条带网的数学模型进行最小二乘平差，直接获得月面巡视探测器的位置与姿态信息。石德乐等(2006)提出了以着陆器为基站，采用立体视觉测量技术以及彩色图像分割的方法，进行跟踪测量的月面巡视探测器定位方法，对惯导系统加里程计的定位方法进行修正，减小月面巡视探测器的计算工作量。马友青等(2014)根据LM算法的核心思想和巡视器图像的构网特征，构建光束法平差模型，克服了高斯牛顿算法适用性弱的缺点。马友青等(2014)基于摄影测量领域中相对定向和绝对定向原理，提出了基于立体图像的月球车导航定位算法。并通过设置连接点坐标观测量权值优化了定位结果。

上述方法中，基于VLBI的定位方法定位精度最优可以达到1m，相对于摄影测量光束法的定位误差较大；而基于摄影测量的定位方法定位结果的精度较高，最优可以达到厘米级，但是基于摄影测量的定位方法往往需要大量的特征点作为计算单元，当导航影像中比较明显的特征点较少时候，则得到的定位结果精度降低，甚至出现迭代求解过程不收敛的情况；基于IMU和里程计定位方法在初始阶段具有较高的定位精度，但是随着巡视探测器的行进，车轮里程计会出现较多的打滑情况，从而导致里程计得到的观测结果出现较大误差，最终影响到巡视探测器的定位结果，而在此过程中IMU测得的角度则不会出现上述情况。基于摄影测量的方法在求解过程中往往将姿态参数作为未知数进行求解，而通过IMU设备可以经过一定的计算得到巡视器的姿态信息，将摄影测量手段结合IMU观测数据可以实现巡视器定位过程的简化。

技术实现要素：

针对上述现有技术存在的不足，本发明提供一种结合IMU和导航影像的月面巡视器快速定位方法。

本发明的技术方案如下：

一种结合IMU和导航影像的月面巡视器快速定位方法，包括如下步骤：

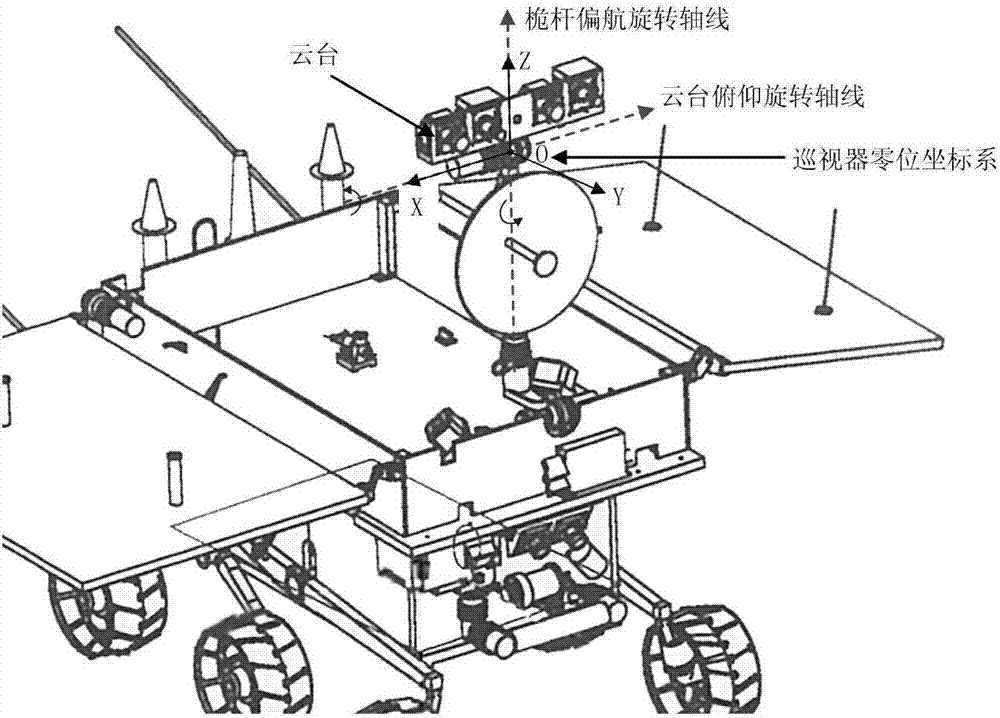
步骤1：构建巡视器零位坐标系；

步骤2：提取导航相机焦距f、导航相机摄影中心与巡视器零位坐标系原点之间的偏移量(B_X，B_Y，B_Z)、巡视器质心与巡视器零位坐标系原点之间的偏移量(ΔX，ΔY，ΔZ)、巡视器俯仰角度、巡视器偏航角度和IMU测得的三轴姿态角；

步骤3：构建像空间辅助坐标系，根据巡视器俯仰角度和巡视器偏航角度计算像空间辅助坐标系相对于巡视器零位坐标系的旋转矩阵R_俯和R_偏；

步骤4：根据IMU的安装参数和地面测试数据计算巡视器零位坐标系与IMU设备在三个坐标轴方向的夹角根据以及巡视器IMU测得的三轴姿态角得到巡视器零位坐标系相对于着陆器当地铅垂坐标系的三个姿态角为简化记为进而得到两套坐标系下的旋转矩阵R_IMU；

步骤5：从选定的导航影像中提取具有明显特征的月面点a，并根据导航相机标定的畸变参数对像点坐标进行误差纠正，得到像点a坐标为(x_a，y_a)；

步骤6：从着陆区数字正射影像DOM及着陆区数字高程模型DEM中提取像点a对应的月面点A在着陆器当地铅垂坐标系下的坐标(X_A，Y_A，Z_A)；

步骤7：按照最小二乘公式X＝(A^TA)^-1A^TL进行求解，得到导航影像摄影中心当地铅垂坐标系坐标(X_S，Y_S，Z_S)，其中：

步骤8：将摄影中心(X_S，Y_S，Z_S)代入下式，得到巡视器质心坐标(X_C，Y_C，Z_C)，完成巡视器定位：

有益效果：本发明提出一种结合IMU和导航影像的月面巡视器快速定位方法，与现有技术相比，具有如下优点：

(1)克服了采用IMU和里程计组合导航定位过程中，由于车轮打滑导致里程计观测值误差增大，从而导致定位误差增大的缺点，同时，由于IMU测角姿态受里程累积影响非常小，克服了采用IMU和里程计组合导航定位精度随里程积累而下降的问题，定位精度优于IMU和里程计组合定位方法；

(2)相对于传统摄影测量定位的方法，本文方法至少只需要1个点即可完成定位，增加了方法的适用情况，解决了月面巡视器在利用摄影测量手段进行定位过程中，当影像中纹理信息匮乏，特征点较少时无法完成定位的问题；

(3)首次真正将IMU设备测得的姿态与摄影测量手段结合，联合组成计算模型进行巡视器的导航定位，方法实现过程简单，耗时少。

附图说明

图1为本发明一种实施方式的结合IMU和导航影像的月面巡视器快速定位方法流程图；

图2为本发明一种实施方式的巡视器零位坐标系示意图。

具体实施方式

下面结合附图对本发明的一种实施方式作详细说明。

如图1所示，本实施方式的结合IMU和导航影像的月面巡视器快速定位方法，包括：

步骤1：构建巡视器零位坐标系，如图2所示，所述零位坐标系原点位于巡视器桅杆偏航旋转轴线与云台俯仰旋转轴线的交点O，X轴与云台俯仰旋转轴线重合，Y轴为桅杆旋转角为零度时刻，在水平面内垂直于云台俯仰旋转轴线向前，Z轴与XY轴构成右手系；

步骤2：提取导航相机焦距f、导航相机摄影中心与巡视器零位坐标系原点之间的偏移量(B_X，B_Y，B_Z)、巡视器质心与巡视器零位坐标系原点之间的偏移量(ΔX，ΔY，ΔZ)、巡视器俯仰角度、巡视器偏航角度和巡视器惯性测量单元(Inertial measurement unit，IMU)测得的三轴姿态角；

如图2所示，巡视器立体视觉系统中的导航相机安装在桅杆上方的云台上，可以在水平方向绕桅杆进行旋转和垂直方向的俯仰。导航影像在拍摄时，为了拍摄周围地形，围绕桅杆进行一定角度的旋转，称为偏航角，记为P；围绕云台旋转轴进行一定角度的旋转，称为俯仰角，记为F。

月面巡视器导航定位是以着陆器当地铅垂坐标系为参考。陆器当地铅垂坐标系原点位于着陆器质心在地面的投影点，Z轴为铅垂线向下方向，XY轴位于与铅垂线垂直的平面内，X轴指向北方向，Y轴指向东方向。三轴方向分别与IMU三轴方向平行。所述IMU测得的三轴姿态角，为当巡视器在某处开展科学考察任务并且需要进行定位时，从IMU设备数据中提取巡视器当前相对于东、北、天顶三个方向的姿态即当前IMU设备与着陆器当地铅垂坐标系的三轴方向的夹角。

步骤3：构建像空间辅助坐标系，根据巡视器俯仰角度和巡视器偏航角度计算像空间辅助坐标系相对于巡视器零位坐标系的旋转矩阵R_俯和R_偏；

以俯仰和偏航后的导航相机摄影中心S为原点，建立像空间辅助坐标系，X轴和Y轴分别平行于导航影像的像平面直角坐标系的x轴和y轴，Z轴与X轴和Y轴构成右手系。

步骤4：根据IMU的安装参数和地面测试数据计算巡视器零位坐标系与IMU设备在三个坐标轴方向的夹角根据以及巡视器IMU测得的三轴姿态角得到巡视器零位坐标系相对于着陆器当地铅垂坐标系的三个姿态角为简化记为进而得到两套坐标系下的旋转矩阵R_IMU；

步骤5：从选定的导航影像中提取具有明显特征的月面点a，并根据导航相机标定的畸变参数对像点坐标进行误差纠正，得到像点a坐标为(x_a，y_a)；

步骤6：从着陆区数字正射影像(Digital Orthophoto Map，DOM)中提取像点a对应的月面点A在着陆器当地铅垂坐标系下的平面坐标(X_A，Y_A)，并从着陆区对应的数字高程模型(Digital Elevation Model，DEM)提取像点a对应的高程坐标Z_A；

步骤7：按照最小二乘求解公式X＝(A^TA)^-1A^TL，计算摄影中心(X_S，Y_S，Z_S)的最优解，其中：

上述最小二乘公式X＝(A^TA)^-1A^TL推导过程如下：

巡视器零位坐标系原点在陆器当地铅垂坐标系下的坐标为(X₀，Y₀，Z₀)，定位采用的导航影像对应的摄影中心坐标在陆器当地铅垂坐标系下的坐标为(X_S，Y_S，Z_S)，该导航相机摄影中心与巡视器零位坐标系原点之间的偏移量为(B_X，B_Y，B_Z)，则可以得到三者间的相互关系如下：

由上式可以得到巡视器零位坐标系原点位置为：

将A点坐标经过旋转和平移后，转换至巡视器零位坐标系下，记为(X_NA，Y_NA，Z_NA)，则可得：

经过旋转和平移，将月面点A由巡视器零位坐标系转换至像空间辅助坐标系下，坐标记为(X_SA，Y_SA，Z_SA)，则有：

导航相机焦距为f，由像点坐标(x_a,y_a)可以得到其在像空间辅助坐标系下的坐标为(x_a,y_a,-f)，则由当前像空间辅助坐标系下摄影中心S(0，0，0)、像点a(x_a,y_a,-f)和对应月面点A(X_SA，Y_SA，Z_SA)在同一直线的约束条件，可得：

化为向量形式为：

将公式(3)、(4)代入公式(6)中可得：

整理为：

根据像点及对应月面点坐标，代入公式(8)中即可得到相机摄影中心S在着陆器当地铅垂坐标系下的坐标(X_S，Y_S，Z_S)。根据公式(8)求解时，只需要一个月面点即可完成摄影中心S坐标的求解。但是实际操作时为避免单点出现误差，往往采用多余观测的手段，因此，需要将公式(8)转为误差方程的形式，根据最小二乘方法求解最优解。令：

则公式(8)可以整理为：

令上式中：

公式可以分解为：

将公式(a)(b)分别除以(c)，并进一步化简为：

将上式进行整理可得：

将未知数(X_S，Y_S，Z_S)整理到方程一侧为：

将公式(13)，改写为误差方程的形式即可按照最小二乘X＝(A^TA)^-1A^TL求解，其中：

步骤8：将摄影中心(X_S，Y_S，Z_S)代入式(16)，得到巡视器质心位置(X_C，Y_C，Z_C)，完成巡视器定位。

式(16)的推导过程为：

巡视器零位坐标系下，由巡视器设计参数得到巡视器质心(X_C，Y_C，Z_C)相对于巡视器零位坐标系原点(X₀，Y₀，Z₀)在三个坐标轴方向的偏移量分别为(ΔX，ΔY，ΔZ)，则可以得到以下关系式：

结合公式(2)，整理可得：

本文方法采用两点定位的结果、经典光束法在巡视器前10个测站的定位结果和二者互差如表1所示：

表1定位结果与互差表

由表1互差可以得出，本发明方法能够有效的完成月面巡视器定位，方法可行且稳定，定位精度高于VLBI相对定位结果。