一种基于时域编解码的高精度动态信号传感和传输方法与流程
本发明属于信号传感和传输技术领域,尤其涉及一种基于时域编解码的高精度动态信号传感和传输方法。
背景技术:
高效精准传感或传输动态信号,尤其是生理时间序列信号和尖峰时间序列信号,可望在大脑及人工神经网络的信息处理、脉冲雷达、通讯领域发挥重大作用。在其他领域,比如生产过程的监视和控制中,也有如何保证尖峰时间序列信号在互相传递和输送过程不失真的问题。
减小系统误差是大幅提高传感和传输精准度的关键。非线性脉冲动态信号传感通常使用静态标定和动态补偿相结合、时域方法测定动态特性辨识动态特性曲线等方式,它们可以降低多种偶然性造成的随机误差或反常误差。然而,作为动态特性补偿的频率域修正法、数值微分法、叠加积分法未考虑误差对处理结果的稳定性。反卷积补偿法、单参数滤波法、多参数模型反滤波法不能采用递归实现,运算量极大。基于虎克定律的线性弹性动力系统或多项式非线性响应系统,不适合外界扰动尤其较大扰补偿动的情形。hammerstein模型采用静态非线性模块和动态线性模块串联降低了问题的复杂性,非线性部分辨识问题转化为参数空间上的函数优化问题,或通过接口送入计算机由软件系统辨识得到动态模型和动态性能指标。但是这些方法带来的系统误差需要大量计算或优异功能的特殊材料来补偿,所以难以兼顾准确、快速、高精度且成本低廉的要求。
近年神经科学、非线性动力学、及时间序列分析的进步使时域编解码生理信号和尖峰脉冲信号成为可能。一类将牛顿运动第二定律用于非线性随机弹性系统导出的非线性自回归整合(nlari)过程,可以被特定为如下时间序列模型:
其中
在那里ω代表外部扰动的期待值,vt代表外部扰动的方差为σ2的高斯白噪音;α>0是阻力系数,β>0是恢复力系数,γ>0是相对恢复力系数,κ1和κ2分别为阻力和恢复力的时间延迟;-xexp(x-2)是一个恢复力项g(x)。考虑κ1=κ2=1,已经证明μt=x0+(ω/α)t。让yt=xt-μt,方程(1)可以改写为如下方程:
(2)当σ=0或vt=0,方程(2)为确定性系统
yt=(1+θ1)yt-1-θ1yt-2+θ2[-yt-1exp(-y2t-1)](3)
已经证明它的稳定性和波动型决于相对恢复力系数γ:当0<γ<1,该系统是一个渐近稳定的零不动点
现有动态信号传感和传输中存在尖峰脉冲信号在互相传递和输送过程失真的问题以及系统误差需要大量计算或优异功能的特殊材料来补偿,难以兼顾准确、快速、高精度且成本低廉的要求。
技术实现要素:
为了解决上述问题,本发明的目的在于提供一种基于时域编解码的高精度动态信号传感和传输方法。
本发明是这样实现的,一种基于时域编解码的高精度动态信号传感和传输方法,所述基于时域编解码的高精度动态信号传感和传输方法使用非线性自回归整合nlari过程建模弹性传感器的动态响应,通过选取满足nlari模型的稳定不动点条件的传感材料使传感器功能相当于一个稳定的不动点传递函数,不动点指它的确定系统方程(3)在时间t的值yt始终等于初值即yt=y0,这意味着初值为零即y0=0以及随机误差为零时,nlari系统的响应输出yt等于外生输入vt即yt=vt,通常情况下vt包括了输入信号和随机误差;通过模拟神经元的动作电压全有全无和反向传播及局部电位可叠加的调节功能,导入调幅逆向脉冲传递函数实现信号重构;以及输入输出相似度(或均方误差等)和信号传输成功率的评价标准。
进一步,稳定不动点域上的传递函数包括:
yt=f(vt):yi-1,t=(2-α)yi-1,t-1-(1-α)yi-1,t-2+βg(yi-1,t-1)+vi-1,t;
以及逆向脉冲传递函数vt=f-1(yt):作为无调幅vi,t=yi-1,t和作为调幅
进一步,所述的传递函数yt=f(vt),包括有界且满足g(-x)=-g(x)和xg(x)<0的恢复力项g(x),阻力系数0<α<2,恢复力系数β>0以及相对恢复力系数
所述的传递函数yt=f(vt)和逆向传递函数vt=f-1(yt),包括输入信号vi,t,响应输出yi,t,yi,t的一阶滞后值yi,t-1,yi,t的二阶滞后值yi,t-2,初始值yi,-1=0,yi,0=0,v1,t=c1如果vt≥c1否则
进一步,输出输入相似度和信号传输成功率作为传感和传输的评价标准中,信号传输成功率
进一步,所述的传感方法,具体的实现步骤包括:
选取能够代表被测量信号特征的时间序列作为输入信号v=(v1,…,vn)′,在计算机上求出参数仿真域,它位于参数域(0,2)作为α,(0,4)作为β,及(0,1)作为γ的某一区域,在那里nlari稳定不动点传递函数的输出y=(y1,…,yn)′和输入v有最大相似度或信号传感成功率;
选取压电材料j=1,…,m制作m个nlari-传感器样品,输入信号v=(v1,…,vn)′到所述传感器样品,测出响应输出
如果
进一步,传输方法,包括计算机传输,nlari-传感器对接收到的输入信号作出响应输出,所述的响应输出经数据化后通过接口送入计算机完成传输;还包括nlari-传感器传输,其具体的实现步骤包括:
步骤一,制作信号传感成功率最大的前p个nlari(α(k),β(k))-传感器样本作为k=1,…,p,使用软件或硬件制作具有的调幅逆向脉冲传递函数功能的调幅器样本,对由nlari(α(k),β(k))-传感器样本的输出作为调幅器样本的输入的串联系统,计算输出v2,t与输入v1,t的信号传感成功率,通过调节阈值c1,c2,c3选取具有最大的信号传感成功率的调幅器样品作为神经元-调幅器样品,与nlari(α(k),β(k))-传感器样本合成为q个相同的nlari(α(k),β(k))-传输器样本;
步骤二,让能够代表被测量信号特征的时间序列信号作为原始输入信号vt进入由q个相同nlari(α(k),β(k))-传输器样品按前一个的输出为后一个输入的方式串联的传输系统,测量它由vt引起的最终输出;
步骤三,计算每次信号传输成功率,重复步骤二,计算信号平均信号传输成功率;
步骤四,选取具有最大平均信号传输成功率的nlari(α(k),β(k))-传输器样本对k=1,…,p作为nlari-传输器。
进一步,传输方法的步骤二,让能够代表被测量信号特征的时间序列信号作为原始输入信号vt进入由q个相同nlari(α(k),β(k))-传输器样品按前一个的输出为后一个输入的方式串联的传输系统,测量它由vt引起的最终输出,具体包括:
选取能够代表被测量信号特征的时间序列作为输入信号vt,在计算机上仿真求出参数仿真域,它在参数域(0,2)作为α,(0,4)作为β和(0,1)作为γ域内,在那里nlari稳定不动点传递函数yt=f(vt|α,β,γ)的输出y=(y1,…,yn)′和输入v=(v1,…,vn)′有最大的传感成功率(尖峰脉冲输入)或相似度(非尖峰脉冲输入)让j=1;
使用压电材料j=1,…,m制作m个传感器样品;
输入信号vt到每个传感器样品中,测出响应
对δyt=θ1,jδyt-1+θ2,jg(yt-1)+vt,使用数据
如果参数估计值
按照本发明提出的技术方案制作的nlari-传感器具有一个稳定不动点的传递函数功能,就是说如果系统初值和随机误差都为零的话,nlari-传感器的响应输出yt等于信号输入vt即yt=vt。所以在理论上nlari-传感器响应输出与信号输入之间只有随机误差,没有确定性结构意义上的系统误差。这样制作的传感器带来的益处是显而易见的,即只要消除随机误差就可完成信号重构。仿真显示nlari-传感器的精度比目前新型的时删传感器在经过动态测量误差补偿后的精度高出很多(详细情形将在具体实施方式一节里描述)。本发明受到大脑神经元传输信号的相关功能的启迪,建立起调幅逆向脉冲传递函数用以消除随机误差,实现对来自nlari-传感器的响应信号重构。在此基础上构成的nlari-传输器仿真三千次尖峰序列信号中继,重复一万次的平均信号传输成功率在稳定不动点的某些域内可以达到98%以上的水平,说明nlari-传感器具有可靠而精确快速的传输性能。由于本发明在理论上确保了多数情形下没有确定性结构意义上的系统误差,所以无须进行频率分析或优化计算等繁琐复杂的非线性动态特性补偿。而且本发明在时域上编解码,因此简单直观,并兼有准确可靠、速度快、精度高、成本低的优点。
附图说明
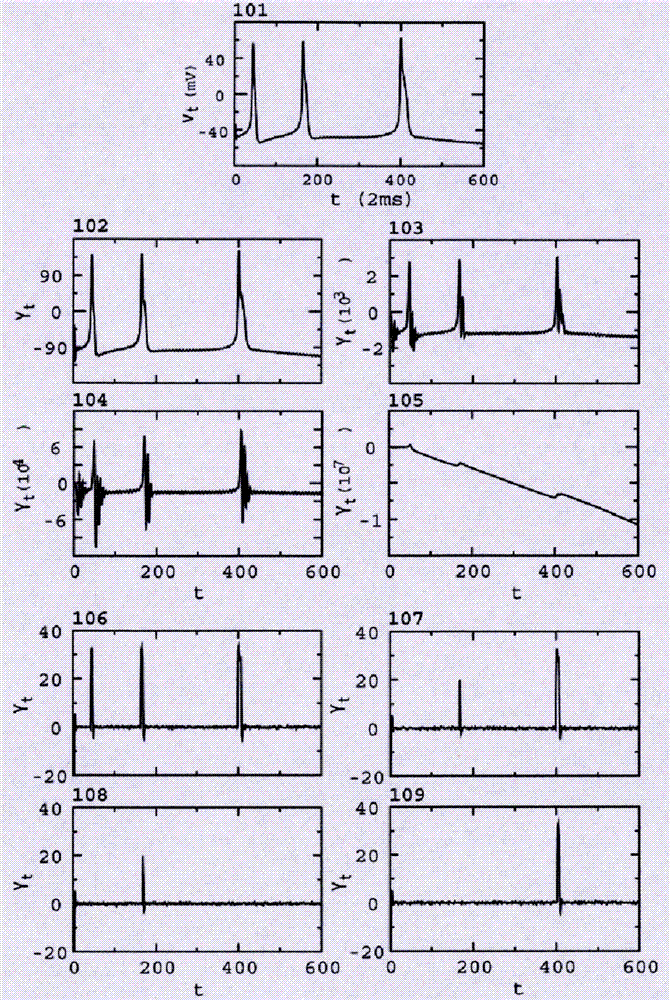
图1是本发明实施例提供的用nlari-传感器在不调节和全有全无调节下经多次传输信号失真的仿真例;
图2是是本发明实施例提供的的nlari-传感器的设计框图;
图3是本发明实施例提供的图2所述的nlari-传感器对临床异常心率的传感仿真例图;
图4是本发明实施例提供的图2所述的nlari-传感器对临床正常与异常心率的传感仿真例图;
图5是本发明实施例提供的针对尖峰脉冲时间序列信号的nlari-传输器的设计框图;
图6是本发明实施例提供的图5所述的nlari-传输器的传输整体效果分步效果及平均传输成功率的仿真例图;
图7是本发明实施例提供的图5所述的nlari-传输器对兴奋性神经元被药物抑制后发射和兴奋性神经元发射的尖峰脉冲序列信号的传输仿真例图。
图8是本发明实施例提供的传感技术与现有传感技术精度比较的一个例子。
图9是本发明实施例提供的基于时域编解码的高精度动态信号传感和传输方法的原理示意图。
具体实施方式
为了使本发明的目的、技术方案及优点更加清楚明白,以下结合实施例,对本发明进行进一步详细说明。应当理解,此处所描述的具体实施例仅仅用以解释本发明,并不用于限定本发明。
本发明实施例提供的基于时域编解码的高精度动态信号传感和传输方法,使用非线性自回归整合nlari过程建模具有随机弹性的传感材料的,稳定不动点域上的nlari传感模型相当于一个传递函数;通过模拟神经元的动作电压全有全无和反向传播及局部电位可叠加的调节功能,导入调幅逆向脉冲传递函数实现信号重构;以及输出入相似度和信号传输成功率评价标准。
稳定不动点域上的传递函数包括:
yt=f(vt):yi-1,t=(2-α)yi-1,t-1-(1-α)yi-1,t-2+βg(yi-1,t-1)+vi-1,t;
以及逆向脉冲传递函数vt=f-1(yt):作为无调幅vi,t=yi-1,t和作为调幅
所述的传递函数yt=f(vt),包括有界且满足g(-x)=-g(x)和xg(x)<0的恢复力项g(x),阻力系数0<α<2,恢复力系数β>0以及相对恢复力系数0<γ=β/(4-2α)<1;
所述的传递函数yt=f(vt)和逆向传递函数vt=f-1(yt),包括输入信号vi,t,响应输出yi,t,yi,t的一阶滞后值yi,t-1,yi,t的二阶滞后值yi,t-2,初始值yi,-1=0,yi,0=0,v1,t=c1如果vt≥c1否则
相似度或输出输入误差的标准差作为传感和传输的评价标准中,信号传感成功率
所述的传感方法,具体的实现步骤包括:
选取能够代表被测量信号特征的时间序列作为输入信号v=(v1,…,vn)′,在计算机上求出参数仿真域,它位于参数域(0,2)作为α,(0,4)作为β,及(0,1)作为γ的某一区域,在那里nlari稳定不动点传递函数的输出y=(y1,…,yn)′和输入v有最大相似度或信号传感成功率;
选取压电材料j=1,…,m制作m个nlari-传感器样品,输入信号v=(v1,…,vn)′到所述传感器样品,测出响应输出
如果
下面结合附图对本发明的应用原理作详细描述。
本发明公开一种时域编解码的高精度动态信号传感和传输方法,它是基于一个非拉普拉斯变换的非线性动态系统传递函数来描述弹性传感器的输入与输出的动态响应关系,以及一个受神经元传输信号功能启发的调幅逆向脉冲传递函数来实现信号重构。nlari的确定结构的稳定性是局部渐进稳定性,尽管不是全局渐进稳定,然而这种稳定性能够满足大多数生物信号和尖峰脉冲信号的无失真传感和传输,尤其通过数据缩小化处理后,效果会更好。本发明通过蒙特卡罗实验发现nlari稳定不动点传递函数的产出并不拘泥于恢复力项g(x)在结构上的细节,只要满足在x轴上有界,并且xg(x)<0和g(-x)=-g(x),更为简单的函数可以替代-x/exp(x2)。
因此,本发明导入nlari稳定不动点传递函数:
yt=f(vt):yt=(2-α)yt-1-(1-α)yt-2+βg(yt-1)+vt
其中,vt代表输入信号,yt代表传递函数的输出,yt-1是yt的一阶滞后值,yt-2是yt的二阶滞后值,由于yt=xt-x0-(ω/α)t,所以yt表示信号与平均水平或均衡状态的偏离,阻力系数0<α<2,恢复力系数β>0,相对恢复系数γ=β/(4-2α)∈(0,1)及κ1=κ2=1。
本发明提出nlari-传感器的设计方法基于使用nlari过程建模弹性传感器的动态响应。比如压电材料在受到外机械力作用下会发生电极化,压电体两端表面内将出现符号相反的束缚电荷。当外力撤去后,它又恢复到不带电的状态。当外力作用方向改变时,电荷的极性随之改变。受力所产生的电荷量与外力的大小成正比。反之,压电材料在受到外电场作用下会发生形变,形变量与外电场强度成正比,表现出与正压电效应类似的现象,不同的是从电能向机械能的转换,压电陶瓷就具有这种机械能与电能之间的转换和逆转换的功能。由此可见,压电材料的正电效应和逆电效应在功能上表现为一个弹性系统,这样制成的传感器功能可以由nlari模型描述。如果选取压电材料的阻力系数α和恢复力系数β位于nlari的稳定不动点域0<γ<1内的,这种传感器的输出输入间的非线性动态响应关系就可以通过稳定不动点上的nlari模型描述,称为nlari稳定不动点传递函数,其中α,β和γ称为传感功能参数。考虑由m个nlari-传感器样本作为中继节点,按上一个节点输出是下一个节点输入的串联方式作信号传递,动态响应关系可描述为yi,t=(2-α)yi,t-1-(1-β)yi,t-2+βg(yi,t-1)+yi-1,t,i表示中继次数(i=1,2,…,q)和t表示信号数(t=1,2,…,n)。
本发明者注意到在不调节和全有全无调节下,经由nlari-传感器样本多次作用后,尖峰脉冲输入信号会发生丢失或歪曲。
如图1所示,初始输入信号序列(如图1的101所示),经过3次(如图1的102所示)、10次(如图1的103所示)和17次(如图1的104所示)nlari-传感器的信号中继仿真后,信号基本上保真,但在经过18次信号中继仿真后信号完全被歪曲(如图1的105所示),即使经过全有或全无律调节,在经过3次(如图1的106所示)、10次(如图1的107所示)和17次(如图1的108所示)和18次(如图1的109)nlari-传感器的信号中继仿真后,信号也被丢失。
本发明使用神经科学的知识来纠正这种信号失真。来自外界的信息被编码成为神经状态时,相关的神经状态可能反映了神经元的解码活动。比如电压门控离子通道开放产生的电流要比刺激输入的电流大;电压刺激随着突触距离和神经递质结合时间的增大呈指数性衰减;受到刺激产生兴奋的轴突与周围静息膜之间的局部电流向两个方向传导(被称之为动作电位的双向传导),产生于轴突或胞体的动作电压向树突丛逆向回传的传播程度随着动作电位的数量和频率的增加而增加,大小取决于阈下兴奋性输入。动作电位反向传播活性可能促进先前冗余电流补充当前被衰减的电压刺激,旨在让信号复原。局部电位的可叠加性使动作电位的反向传播功能得以实现。可以总结如下:动作电位的反向传播活性和全有全无律、以及局部电位的可叠加性暗示了神经元可能具有功能(i)高于阈值的任何强度对刺激神经元响应是相同的;(ii)没有达到阈值的神经元不会点火;(iii)先前冗余电流的回流补充当前衰减的信号电流以促使信号重构。功能(i)源于生物的有效性和节能性;功能(ii)防止噪音混入信号,功能(iii)避免信号衰减。因此,针对尖峰脉冲信号重构,导入逆向脉冲传递函数vt=f-1(yt):作为少数几个中继节点的传输,它可以是无调节函数f-1=i,即vi,t=yi-1,t,初始值yi,-1=yi,0=0及y0,t=vt;作为有很多中继节点的传输:vt=f-1(yt)为如下调幅逆向脉冲传递函数
其中yi-1,t=(2-α)yi-1,t-1-(1-α)yi-1,t-2+βg(yi-1,t-1)+vt-1,t,阀值0<c3<c2<c1,初始值yi,-1=yi,0=0,v1,t=c1如果vt≥c1否则
下面结合附图和具体实施例对本发明进一步描述。
本发明提出的nlari-传感器可按如下具体步骤实现:
第一步选取能够代表被测量信号特征的时间序列作为输入信号vt,在计算机上仿真求出参数仿真域,它在参数域(0,2)作为α,(0,4)作为β和(0,1)作为γ域内,在那里nlari稳定不动点传递函数yt=f(vt|α,β,γ)的输出y=(y1,…,yn)′和输入v=(v1,…,vn)′有最大的传感成功率(尖峰脉冲输入)或相似度(非尖峰脉冲输入)(如图2的201所示)。让j=1;
第二步使用压电材料j=1,…,m制作m个传感器样品(如图2的202所示);
第三步输入信号vt到每个传感器样品中,测出响应
对δyt=θ1,jδyt-1+θ2,jg(yt-1)+vt(5)
使用数据
作为j=1,…,m(如图2的204所示);
第四步如果参数估计值
第五步选择具有最大输出输入相似度或信号传感成功率的传感器样品作为nlari-传感器(如图2的207)。
图3显示了临床异常心率hrv序列作为信号输入(301、303、305)和它们经由nlari-传感器的仿真输出(302、304、306),仿真输出与输入的心率hrv展示了很高的相似度。图4显示了较高频率的正常与临床异常心率hrv序列作为输入信号(401、403、405),类似地,这些心率信号输入与它们的nlari-传感器的仿真输出(402、404、406)有很高相似度。图3和图4的仿真基于具有α=1.1159、β=0.7625、γ=0.4312的传递函数,包括本发明申请书中所有仿真例都是基于g(x)=-x/(1+x4)的稳定不动点传递函数。
本发明提出两个方案实现尖峰脉冲信号传输,方案1是nlari-传感器的输出被数据化后通过接口送入计算机(图5的501),由计算机完成信号传输(图5的502)。
方案2是nlari-传输器方法,结合附图5-8说明它的实现步骤如下:
第一步基于传感功能参数α(k)和β(k),制作信号传感成功率最大的前p个传感器样品,记为nlari(α(k),β(k))-传感器样本,简称nlari-传感样品(k=1,…,p)(如图5的503所示),让k=1;
第二步考虑q个相同的nlari(α(k),β(k))-传感器样本,通过软件或硬件制作具有功能
yi-1,t=(2-α)yi-1,t-1-(1-α)yi-1,t-2+βg(yi-1,t-1)+vi-1,t
其中,vi-1,t和yi-1,t分别表示经第i-1个nlari(α(k),β(k))-传感器样本的输入和输出的第t个信号,初始值yi,-1=yi,0=0,v1,t=c1如果vt≥c1否则
第三步让k=k+1,重复第二步直到k=p,获得q个相同的nlari(α(k),β(k))-传输器样品(图5的505所示),让k=1;
第四步对代表被测量信号特征的尖峰脉冲时间序列信号vt,测量由q个传输器样品按前一个的输出作为后一个输入的方式串联起来的最终输出(图5的506所示);
第五步计算串联实验的信号传输成功率,重复第四步获得平均传输成功率(图5的507所示);
第六步如果k<p,让k=k+1,返回第四步(如图5的508所示),否则选取有最大的平均信号传输成功率的传输器样品作为nlari-传输器(如图5的509所示)。
为区别于数据传输,本发明不采用误码率作传输精确性指标,而导入如下信号传输成功率
其中,w0=(w0,1,…,w0,n)′表示初始输入信号,wq=(wq,1,…,wq,n)′表示经过q次中继节点后的输出信号,w0,t=1如果vt≥c3否则w0,t=0,wq,t=1如果yq,t≥c3否则wq,t=0,vt是原始输入信号。特别当q=1时,信号传输成功率(7)被称为信号传感成功率。对于只有几个节点的传输,nlari-传输器可以不含调幅解码器。图6的601显示了输入的尖峰脉冲时间序列信号经nlari-传输仿真一百次、三千次信号中继的传输成功率,它是随机信号生成器产出一万个时间序列的传输成功率的平均值。在仿真参数域γ∈(0.306,0.412)∪(0.652,0.825),α∈(0.885,0.845)∪(0.755,0.690),β∈(0.682,0.952)∪(1.623,2.160),c1∈(0.0014,0.0016),c2∈(0.0009,0.0011),c3∈(0.0007,0.0009)上,信号传输成功率分别达到了99.00%和99.99%以上的高精度。为说明这些精确传输是如何实现的,图6显示了信号生成器的一次随机实现作为一个信源(如图6的602所示)、接收的初始刺激(如图6的603所示)、第一次对刺激输入的响应(如图6的604所示)和第一次的信号重构(如图6的605所示)、第3000次对刺激输入的响应(如图6的606所示)和第3000次的信号重构(如图6的607所示)。人们可以看到每次响应都大致准确,但存在一些误差,调幅逆向传递函数消除了响应误差。图7显示了被注射(即兴奋性神经元被药物抑制,如图701所示)和未被注射丹皮酚的兴奋性神经元发射(如图703)的尖峰脉冲序列信号分别作为初始输入信号,经nlari-传输器仿真3000次中继达到无失真传输(如图702和704所示)。
为了说明本发明提高的传感精度的效果,图8显示了nlari-传输器的精度(如图8的801所示)与一种新型的时删传感器在经过动态测量误差补偿后的精度的一个比较(如图8的802所示)(详细情况请参考“时删传感器动态测量误差补偿”,光学精密工程,第23卷,第4号,2015年4月)。时删传感器的动态测量误差主要包括了具有周期性的系统误差和不具有确定性的随机误差。作者通过傅立叶逼近模型对周期性的系统误差进行分离,使用最小二乘法求解超定方程组的方法推定系统误差补偿参数,以及建立灰色预测模型对随机性成份进行预测和补偿。在相同的实验条件下,对三台不同传感器进行了误差补偿后的最终误差对比。尽管仿真误差要比实体误差小很多,但是nlari-传输器的精度还是明显高于时删传感器的精度。
以上所述仅为本发明的较佳实施例而已,并不用以限制本发明,凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等,均应包含在本发明的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!