一种基于故障诊断的轨道交通车辆轴承剩余寿命预测方法与流程

本发明涉及轨道交通车辆轴承的故障诊断及剩余寿命预测领域。更具体地，涉及一种基于故障诊断的轨道交通车辆轴承剩余寿命预测方法。

背景技术：

轨道交通的高速发展，对车辆的安全性和可靠性提出了更高的要求。早晚高峰时段很多运营线路均在超负荷运行，这就要求列车各个关键系统必须安全可靠，不能出现故障或是失效状态下运行的现象。轴承是轨道交通中不可缺少的元件之一，同时也是最易损坏的元件，其有效性直接导致列车的运行安全。复杂时变的运行环境：载荷，轨道的平顺程度、温度等，对于轴承的健康状态有很大的影响。当轴承中某一部位发生故障时，会产生连锁反应，轻则导致车辆的相关系统受损，重则会导致车辆的停运甚至是人员的伤亡。

在现有的剩余寿命预测研究中，较少的考虑到故障类型对于剩余寿命预测的影响。当故障发生后轴承进入快速衰退状态，而不同故障状态下轴承的衰退特性大不相同，剩余寿命预测的结果也大不相同。

因此，需要提供一种基于故障诊断的轨道交通车辆轴承剩余寿命预测方法。

技术实现要素：

本发明的目的在于提供一种基于故障诊断的轨道交通车辆轴承剩余寿命预测方法，以实现轴承发生早期故障的故障检测、故障分离及剩余寿命预测，为车辆轴承维修决策的制定提供依据。

为达到上述目的，本发明采用下述技术方案：

一种基于故障诊断的轨道交通车辆轴承剩余寿命预测方法，包括如下步骤：

s100、使用局部均值分解法将轴承振动信号分解为若干pf单分量，对分离出的单分量进行时域、频域、能量及统计量的多角度特征值提取，将提取到的多角度特征值使用主成分分析法降维与融合；

s200、进行基于循环平稳理论的故障诊断；

s300、通过进行多变量模型训练实现基于多变量模型的故障分离；

s400、基于半监督算法，协同使用bp神经网络和支持向量回归两种算法进行基于故障诊断的剩余寿命预测。

优选地，所述使用局部均值分解法将轴承振动信号分解为若干pf单分量进一步包括：

s111、寻找轴承振动信号x(t)所有局部极值点ni，将上下极值点分别用三次样条曲线进行连接，得到信号的上、下包络线emax、emin，计算局部均值函数m11(t)和包络函数c11(t)：

s112、从x(t)中分离出局部均值函数m11(t)，得到：

h11(t)＝x(t)-m11(t)；

s113、对h11(t)解调，将h11(t)除以包络函数c11(t)得到：

s114、按照s111中的方法求出s11(t)所对应的包络函数c12(t)，若包络函数c12(t)＝1，则判断s11(t)为纯调频函数；若包络函数c12(t)≠1，则迭代执行上述步骤s111-s113，直至s1n(t)的包络估计函数c1(n+1)(t)＝1，则有：

s115、将进行迭代处理过程中产生的所有包络函数相乘得包络信号：

s116、令包络信号c1(t)与纯调频函数s1n(t)相乘，得到x(t)的第一个pf分量pf1：

pf1(t)＝c1(t)·s1n(t)；

s117、从x(t)中分离出第一个分量pf1后得到一个新的待分解信号r1(t)，将新的待分解信号替代轴承振动信号迭代执行步骤s111-s116，直至新的待分解信号rk(t)为一单调函数为止，k代表迭代次数，即

至此，x(t)被分解为k个pf分量及一个单调函数rk(t)之和：

优选地，所述多角度特征值包括时域特征值、频域特征值、统计特征参数特征值和能量特征值；所述时域特征值包括均方值、方差、峰值、峭度、偏度、脉冲因子、峰值因子和裕度因子；所述频域特征值包括均方频率、频谱重心、频率方差和频率标准差；所述统计特征参数特征值包括威布尔形状参数、威布尔尺度参数、伽马形状参数和伽马尺度参数；所述能量特征值包括香农熵和能量矩。

优选地，所述将提取到的多角度特征值使用主成分分析法降维与融合进一步包括：

s131、设多角度特征值构成的数据的样本数为n，每个样本包含p个特征向量，样本矩阵为xnxp，对数据进行标准化：

其中，i＝1,2,…,n；；j＝1,2,…,p；；

s132、计算特征向量的协方差矩阵r，并计算其特征值和特征向量：

r＝y^ty/(n-1)

其中，y是标准化后的数据，计算出r的特征值分别为λ1≥λ2≥…≥λp，以及其对应的特征向量为αi＝(αi1,αi2,…,αip)^t,i＝1,2,…p；

s133、设正交空间中前k个主元分量为y1,y2…yk，计算累计方差贡献率：

至此，完成了将p维数据降至k维数据，实现了多角度特征值降维与融合。

优选地，步骤s200进一步包括：

s211、对于为非平稳随机信号的轴承振动信号x(t)，x(t)的时变自相关函数的表示为：

其中，τ为时延因子，e{·}表示统计平均，*表示复共轭；

s212、设rx(t,τ)以t为周期，用样本平均代替统计平均，将时变自相关函数表示为：

将上式用傅里叶级数展开表示为：

其中α＝m/t(m∈z)为循环频率，其傅里叶系数为

s213、设t0＝(2n+1)t，通过整理可以得到循环自相关函数为：

r(τ,α)＝<x(t+τ/2)x^*(t-τ/2)e^-j2παt>t；

s214、得到循环谱相关密度函数并根据循环谱相关密度函数进行基于循环平稳理论的故障诊断，循环谱相关密度函数为：

其中，f为谱频率。

优选地，步骤s300进一步包括：

进行多变量模型训练：

s311、针对具有h种故障类型的数据，样本总数为n，每种故障下样本数为[n1,n2,…nh]；

s312、对于不同故障状态的所有样本进行振动数据特征提取，使用拉普拉斯分值法对所有特征值进行选取，每种故障都选出p个最优特征量，分别为x＝[x1,x2,…,xp]

s313、设模型类型m＝1，0＜m＜4，模型阶数r＝1，0＜r＜p-1，设h＝1；

s314、对第h(1≤h≤h)类训练样本执行：选择特征量xi为被预测变量，选择r个特征量xj(j≠i)为预测变量，则共有种选择方案，即对于被预测变量来说可建立中预测模型；

s315、第h类故障类型共有nh个训练样本，对于每种组合方式，被预测变量xi都可以建立nh个方程，使用最小二乘法对模型bo,bj,bjj,bjk进行参数估计，得到每种组合下的被预测变量的数学方程

s316、计算每种组合下所有样本对xi的估计误差和其中l表示第l个训练样本，共有个sse值，选择最小的sse对应的预测模型为该种故障，则模型类型为m且阶数为r的条件下，变量xi的预测模型已确定；

s317、令h＝h+1，迭代执行步骤s313-s316，直到h＝h；

s318、令r＝r+1，迭代执行s314-s317直到r＝p-1；

s319、令m＝m+1，迭代执行s314-s318直到m＝4，得到了各种模型类型及各种阶次条件下的预测模型即每个m和r的条件下都会得到h*p个组成矩阵，然后将训练变量回代各个方程，选择最小误差值下的m和r对应的矩阵为本次的训练输出模型；

进行故障类型预测：

s321、对预测样本计算同样的p个最优特征量，分别为x＝[x1,x2,…,xp]；

s322、将特征值带入训练好的数学模型，得到预测的估计变量值其中h＝[1,2,…,h]，i＝[1,2,…,p]；

s323、计算每种类型下，所有估计变量的误差值之和sse^h最小误差值的状态类型为该待预测数据的故障类型。

优选地，步骤s400进一步包括：

s411、将故障数据等间隔取值，3/4作为训练数据l，剩余1/4作为验证数据y，使用故障数据l对bp神经网络和支持向量回归两种算法进行训练，得到预测训练模型h1和h2；

s412、从未标记数据库中选取未标记数据yi：，使用第j种算法对其进行预测，得到预测输出值，并将第i组未标记数据及其预测的输出与故障数据l组合成新的故障数据；

s413、使用步骤s412得到的新的故障数据对模型重新训练得到新的网络hj’；

s414、使用验证数据y进行验证，将y输入hj，计算输出值与实际值之间的均方差，记为eij，再将y输入hj’，计算输出值与实际值之间的均方差，记为ej’，然后计算eij-eij’的值，记为eij；

s415、迭代执行步骤s412-s414直到数据库中没有未标记数据为止；

s416、判断所有的eij中是否有大于0的值，如没有则重新回到s411步对另一种算法进行训练；若存在大于0的值则选择最大的eij对应的那组未标记数据和网络的输出数据，将其作为伪标记数据，与原有的故障数据组合成新的故障数据组lj’，并将第i组未标记数据从未标记数据库中移除；对另一种算法进行s412-s415的训练，进入下一步；

s417、判断两种算法训练后l值是否都有更新，若是则交换两种算法的故障数据作为彼此的故障数据，重新进行步骤s411-s416，直到达到迭代次数t为止，若否则结束训练，进行下一步；

s418、对得到的两种网络进行权值优化，两种算法输出值加权后作为最后的网络输出，得到轴承剩余寿命预测值。

本发明的有益效果如下：

本发明所述技术方案充分的考虑到不同故障下轴承衰退模式之间的不同，提高了剩余寿命预测的精度，建立了一整套的轴承故障状态检测与预测体系，完善了对的轴承健康状态监测。使用循环平稳及多变量预测模型进行故障诊断，充分的利用了轴承振动信号的二阶循环特性及特征值之间的内在关系。使用基于半监督的协同训练解决了故障数据难以获取的问题。为轴承后期的维修提供了支持。

附图说明

下面结合附图对本发明的具体实施方式作进一步详细的说明；

图1示出基于故障诊断的轨道交通车辆轴承剩余寿命预测方法流程图。

图2示出轴承振动信号的时域波形图。

图3示出轴承振动信号的频域波形图。

图4示出轴承振动信号的能量波形图。

图5示出轴承振动信号的统计特征波形图。

图6示出特征值融合后的主元成分示意图。

图7示出部分特征值波动点标记示意图。

图8示出不同特征频率下的谱相关密度函数最大值示意图。

图9示出不同特征频率下的谱相关密度函数切片示意图。

图10示出基于bp神经网络、svr及半监督算法的剩余寿命预测曲线图。

图11示出不同未标记数据下半监督算法的剩余寿命预测曲线图。

图12示出故障后基于不同未标记数据下的半监督算法的剩余寿命预测曲线放大图。

具体实施方式

为了更清楚地说明本发明，下面结合优选实施例和附图对本发明做进一步的说明。附图中相似的部件以相同的附图标记进行表示。本领域技术人员应当理解，下面所具体描述的内容是说明性的而非限制性的，不应以此限制本发明的保护范围。

本发明公开的基于故障诊断的轨道交通车辆轴承剩余寿命预测方法需要对实时采集的振动数据进行分析，通过多角度特征综合处理，提取出能明显表现故障的特征。利用旋转机械振动信号具有循环平稳特性进行故障检测，根据不同故障状态下特征值之间的内在关系使用多变量模型进行模式识别判断故障类型，最后将故障诊断的结果输入不同剩余寿命预测模型，剩余寿命预测主要使用半监督协同训练的算法。

本发明公开的基于故障诊断的轨道交通车辆轴承剩余寿命预测方法相对于已有的剩余寿命预测算法，充分的考虑到了故障类型对于寿命预测结果的影响，结合故障诊断结果对轴承进行剩余寿命预测。对于传统的时域、频域以及时频域故障检测方法中，忽略了旋转机械具有不同于其他机械的运转模式，而这种循环往复的运行方式将产生具周期性的振动信号，包含了大量的状态信息。轴承振动信号的二阶统计量具有周期性变化的特性，因此基于轴承的循环平稳特性，结合经典周期图法的计算方法，使用基于周期图估计循环谱相关密度函数进行轴承的早期故障检测。在故障分离方面充分考虑到不同故障状态下特征值之间具有不同内在关系这一特性，使用多变量预测模型的模式识别法，解决了现有的基于神经网络和支持向量机法在参数设置和核函数选取方面的限制。

本发明公开的基于故障诊断的轨道交通车辆轴承剩余寿命预测方法，考虑到目前全生命周期数据难以获取，而大量的未故障状态下数据较容易采集的情况，充分利用未故障状态下的数据信息，使用半监督原理提高算法的预测能力。此外基于现有算法之间的差异，使用bp神经网络及支持向量回归两种算法进行协同训练，防止了算法训练过程中的误差传递。剩余寿命算法中的输入为特征值，输出为剩余寿命值，故障数据已知其输出，记为标记数据；未故障状态下数据的输出未知，记为未标记数据(ul)。

本发明公开的基于故障诊断的轨道交通车辆轴承剩余寿命预测方法以试验平台下的滚动轴承垂向振动加速度为分析对象，主要研究轴承基于故障诊断下的剩余寿命预测。前期使用特征值多角度提取与融合技术，反映轴承的状态特征；通过对循环谱相关密度函数的计算，进行故障的早期检测，结合故障状态下的数据对故障轴承进行模式识别。最后将故障诊断的结果输入剩余寿命预测算法中，对故障早期时刻某种故障模式下的轴承进行剩余寿命预测，实现了轴承可使用时间的预测。

本发明公开的基于故障诊断的轨道交通车辆轴承剩余寿命预测方法包括如下步骤：

s100、进行多角度特征值提取与融合：

在特征提取方面先使用局部均值分解(localmeandecomposition,lmd)法将轴承振动信号分解为若干pf单分量；对分离出的单分量进行时域、频域、能量及统计量的多角度特征值提取；最后将提取到的多角度特征值使用主成分分析法(principalcomponentanalysis,pca)降维与融合。

步骤s100的具体过程为：

首先，进行局部均值分解：

s111、寻找轴承振动信号(原始信号)x(t)所有局部极值点ni，将上下极值点分别用三次样条曲线进行连接，得到信号的上、下包络线emax、emin，计算局部均值函数m11(t)和包络函数c11(t)：

s112、从x(t)中分离出局部均值函数m11(t)，得到：

h11(t)＝x(t)-m11(t)；

s113、对h11(t)解调，将h11(t)除以包络函数c11(t)得到：

s114、按照s111中的方法求出s11(t)所对应的包络函数c12(t)，若包络函数c12(t)＝1，则判断s11(t)为纯调频函数；若包络函数c12(t)≠1，则迭代执行上述步骤s111-s113，直至s1n(t)的包络估计函数c1(n+1)(t)＝1，则有：

s115、将进行迭代处理过程中产生的所有包络函数相乘得包络信号：

s116、令包络信号c1(t)与纯调频函数s1n(t)相乘，得到x(t)的第一个pf分量pf1：

pf1(t)＝c1(t)·s1n(t)；

s117、从x(t)中分离出第一个分量pf1后得到一个新的待分解信号r1(t)，将新的待分解信号替代轴承振动信号迭代执行步骤s111-s116，直至新的待分解信号rk(t)为一单调函数为止，k代表迭代次数，即

至此，x(t)被分解为k个pf分量及一个单调函数rk(t)之和：

在进行局部均值分解之后，进行多角度特征值提取：

在多角度特征提取中本发明提取18个特征值，包括：

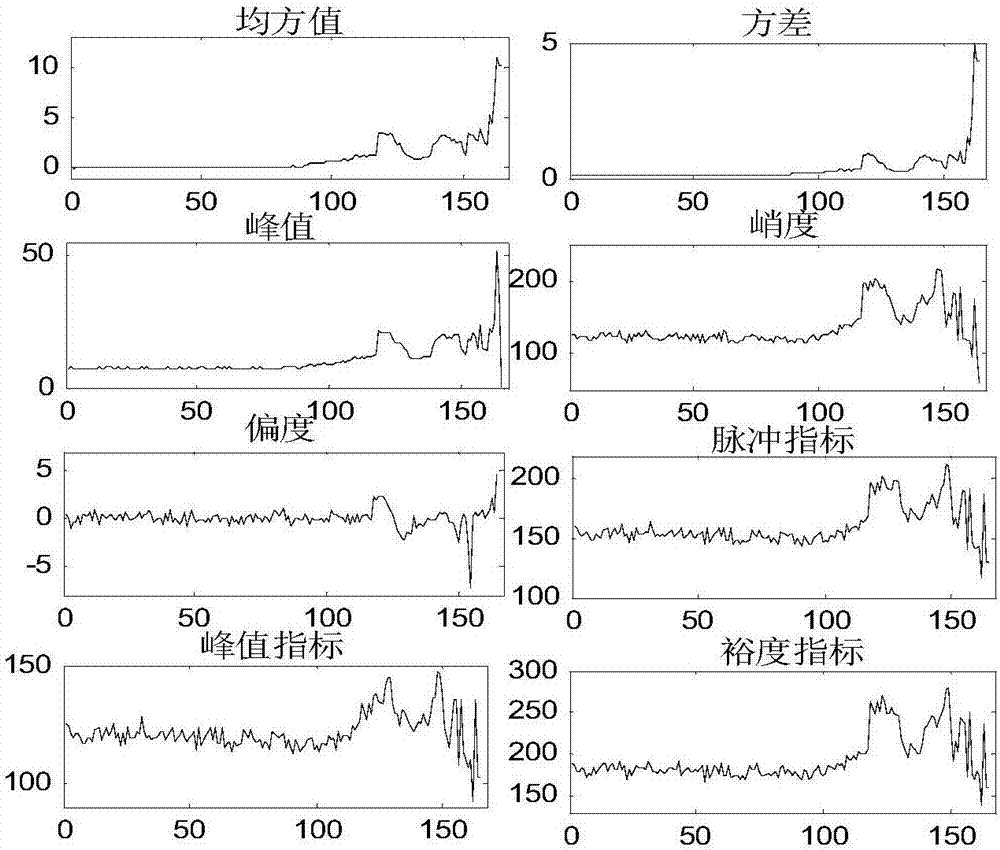
时域特征值包括反映运行状态全局特性并判断轴承是否故障的均方值、方差、峰值、峭度、偏度、脉冲因子、峰值因子和裕度因子等；

频域特征值包括描述信号频域特征的变化并反映轴承的故障部位的均方频率、频谱重心、频率方差和频率标准差等；

统计特征参数特征值包括威布尔形状参数、威布尔尺度参数、伽马形状参数和伽马尺度参数等；

能量特征值包括香农熵(shannonentropy)和能量矩

在进行多角度特征值提取之后，进行多角度特征值降维与融合：

特征值降维与融合方面使用pca法，主要过程如下：

s131、设多角度特征值构成的数据的样本数为n，每个样本包含p个特征向量，样本矩阵为xnxp，对数据进行标准化，以降低不同特征值不在同一数量级的问题：

其中，i＝1,2,…,n；；j＝1,2,…,p；；

s132、计算特征向量的协方差矩阵r，并计算其特征值和特征向量：

r＝y^ty/(n-1)

其中，y是标准化后的数据，计算出r的特征值分别为λ1≥λ2≥…≥λp，以及其对应的特征向量为αi＝(αi1,αi2,…,αip)^t,i＝1,2,…p；

s133、设正交空间中前k个主元分量为y1,y2…yk，计算累计方差贡献率：

至此，完成了将p维数据降至k维数据，实现了多角度特征值降维与融合。

s200、进行基于循环平稳理论的故障诊断，具体过程如下：

s211、对于为非平稳随机信号的轴承振动信号x(t)，x(t)的时变自相关函数的表示为：

其中，τ为时延因子，e{·}表示统计平均，*表示复共轭；

s212、设rx(t,τ)以t为周期，用样本平均代替统计平均，将时变自相关函数表示为：

将上式用傅里叶级数展开表示为：

其中α＝m/t(m∈z)为循环频率，其傅里叶系数为

s213、设t0＝(2n+1)t，通过整理可以得到循环自相关函数为：

r(τ,α)＝<x(t+τ/2)x^*(t-τ/2)e^-j2παt>t；

s214、得到循环谱相关密度函数并根据循环谱相关密度函数进行基于循环平稳理论的故障诊断，循环谱相关密度函数(spectralcorrelationdensity，简称scd)是自相关函数关于时延的fourier变换，如下式所示：

其中，f为谱频率。

s300、通过进行多变量模型训练和故障类型预测实现基于多变量模型的故障分离：

对于vpmcd而言可以选择的模型如下，

线性模型(l)：

线性交互模型(li)

二次交互模型(qi)

二次模型(q)

vpmcd具体操作步可分为进行多变量模型训练和故障类型预测两步，模型训练阶段需要通过对比分析，从可选择的模型中选择最优的变量的预测模型。

步骤s300的具体过程如下：

首先进行多变量模型训练：

s311、针对具有h种故障类型的数据，样本总数为n，每种故障下样本数为[n1,n2,…nh]；

s312、对于不同故障状态的所有样本进行振动数据特征提取，使用拉普拉斯分值法对所有特征值进行选取，每种故障都选出p个最优特征量，分别为x＝[x1,x2,…,xp]；

s313、设模型类型m＝1，0＜m＜4，模型阶数r＝1，0＜r＜p-1，设h＝1；

s314、对第h(1≤h≤h)类训练样本执行：选择特征量xi为被预测变量，选择r个特征量xj(j≠i)为预测变量，则共有种选择方案，即对于被预测变量来说可建立中预测模型；

s315、第h类故障类型共有nh个训练样本，对于每种组合方式，被预测变量xi都可以建立nh个方程，使用最小二乘法对模型bo,bj,bjj,bjk进行参数估计，得到每种组合下的被预测变量的数学方程

s316、计算每种组合下所有样本对xi的估计误差和其中l表示第l个训练样本，共有个sse值，选择最小的sse对应的预测模型为该种故障，则模型类型为m且阶数为r的条件下，变量xi的预测模型已确定；

s317、令h＝h+1，迭代执行步骤s313-s316，直到h＝h；

s318、令r＝r+1，迭代执行s314-s317直到r＝p-1；

s319、令m＝m+1，迭代执行s314-s318直到m＝4，得到了各种模型类型及各种阶次条件下的预测模型即每个m和r的条件下都会得到h*p个组成矩阵，然后将训练变量回代各个方程，选择最小误差值下的m和r对应的矩阵为本次的训练输出模型。

之后，进行故障类型预测：

s321、对预测样本计算同样的p个最优特征量，分别为x＝[x1,x2,…,xp]；

s322、将特征值带入训练好的数学模型，得到预测的估计变量值其中h＝[1,2,…,h]，i＝[1,2,…,p]；

s323、计算每种类型下，所有估计变量的误差值之和sse^h最小误差值的状态类型为该待预测数据的故障类型。

s400、基于半监督算法，协同使用bp神经网络和支持向量回归两种算法进行基于故障诊断的剩余寿命预测：

使用bp神经网络和支持向量回归两种算法进行半监督的协同循环训练，主要步骤如下：将故障数据等间隔取值，3/4作为训练数据l，剩余1/4作为验证数据y。步骤s400的具体过程为：

s411、初始化：使用故障数据l对bp神经网络和支持向量回归两种算法进行训练，得到预测训练模型h1和h2；

s412、从未标记数据库中选取未标记数据yi：，使用第j种算法对其进行预测，得到预测输出值，并将第i组未标记数据及其预测的输出与故障数据l组合成新的故障数据，其中第j种算法为神经网络算法或支持向量回归算法，用第j种算法来表示是为了后面参数表述方便；

s413、使用步骤s412得到的新的故障数据对模型重新训练得到新的网络hj’；

s414、使用验证数据y进行验证，将y输入hj，计算输出值与实际值之间的均方差，记为eij，再将y输入hj’，计算输出值与实际值之间的均方差，记为ej’，然后计算eij-eij’的值，记为eij；

s415、迭代执行步骤s412-s414直到数据库中没有未标记数据为止；

s416、判断所有的eij中是否有大于0的值，如没有则重新回到s411步对另一种算法进行训练；若存在大于0的值则选择最大的eij对应的那组未标记数据和网络的输出数据，将其作为伪标记数据，与原有的故障数据组合成新的故障数据组lj’，并将第i组未标记数据从未标记数据库中移除；对另一种算法进行s412-s415的训练，进入下一步；

s417、判断两种算法训练后l值是否都有更新，若是则交换两种算法的故障数据作为彼此的故障数据，重新进行步骤s411-s416，直到达到迭代次数t为止，若否则结束训练，进行下一步；

s418、对得到的两种网络进行权值优化，两种算法输出值加权后作为最后的网络输出，得到轴承剩余寿命预测值。

下面代入具体的轴承振动信号对本发明公开的基于故障诊断的轨道交通车辆轴承剩余寿命预测方法作进一步地说明。

本发明公开的基于故障诊断的轨道交通车辆轴承剩余寿命预测方法包括如下步骤：

s100、进行多角度特征值提取与融合：

采集轴承全生命周期数据，使用lmd法对轴承振动信号进行分解，对得到的单分量进行多角度特征值提取，以pf1分量为例，如图2所示为轴承时域特征值、图3所示为轴承频域特征值、图4所示为轴承能量特征值、图5所示为轴承统计特征值，共提取18种特征值。通过全生命周期的特征值图可以看到每个特征值都能够反映出轴承的运行状态，即在轴承运行初期特征值均显示平稳状态，没有较大波动，但当轴承运行一段时间后特征值开始有波动，呈现向上(向下)的趋势且斜率逐渐增大(减小)

对计算的特征值进行pca融合降维，取贡献率为95％的主元成分，结果如图6所示，共得到六维主元。可以看出这些分量都完好的保存了轴承数据退化的状态。

s200、进行基于循环平稳理论的故障诊断：

以均方值、方差、峰值和峭度四个时域特征指标为例，标记出有微弱波动的时刻如图7所示。四个特征值的时刻各不相同，最早的在99h处，最晚的在109h处，相差间隔为10小时，对于城轨列车轴承来说，10小时内一直处于故障状态运行，会带来极大的危险。此外四个特征值在118h处均出现较大波动，说明轴承已经处于较为严重的故障状态。通过计算，轴承外圈故障频率为236.4hz，内圈故障频率为296.8hz，转频为33.33hz，滚珠故障频率为139.9hz，保持架故障频率为14.8hz。计算各特征频率处的最大谱相关密度函数值如图8所示，从图中可以看出，只有外圈故障频率处在89.67处有明显的波动，其他频率处一直保持平稳状态。

使用89.67处轴承振动信号进行谱切片分析，如图9所示。外圈故障频率附近谱密度相关切片图中237.4hz处的幅值最大，此处237.4hz与理论的外圈故障频率236.4hz存在一定的差异，主要是由于转速的波动和实际承载间的变化造成实际故障频率与理论故障频率的差异；同理将内圈、滚动体、保持架故障频率及转频附近的谱密度相关切片中能量最大的切片取出。将取出的最大能量切片组合，图中可以看出只有外圈故障频率处的切片幅值最高，因此判定该轴承外圈发生故障。

s300、通过进行多变量模型训练和故障类型预测实现基于多变量模型的故障分离：

选择特波形因子，峭度指标，功率谱重心指标，均值频率，均方谱作为特征值。其中训练数据每种状态40个样本，测试数据每种状态10个样本。数据准备好后根据vpmcd的流程进行模型训练。再将89.67处的振动信号同样进行特征值计算，输入训练好的数学模型中，计算每种状态下5个特征值的估计误差总和，对每种状态下误差之和进行对比，选择误差最小的一种状态作为该测试数据的真正状态，测试结果，即轴承89.67小时处的信号故障分离结果如表1所示，结果与实际相符。对10个测试样本进行预测，使用bp神经网络和支持向量机算法与vpmcd在训练时间、测试结果的准确度上进行对比分析如表2所示。

表1

表2

s400、协同使用bp神经网络和支持向量回归两种算法进行基于故障诊断的剩余寿命预测：

使用经过粒子群优化后的bp神经网络和支持向量回归作为协同训练的两种算法，使用另外8组未标记数据以及一组外圈故障数据最为算法的训练样本，使用检测到故障的数据作为测试样本。

使用两点的特征值作为网络模型的输入，两点即为当前点对应的特征值和前一时刻监测点对应的特征值，维数为12；输出为剩余寿命值，维数为1。

对单独使用bp神经网络和支持向量回归时的预测结果与使用8个未标记数据时的预测结果进行对比，如图10所示；此外针对不同的未标记数据个数对于算法精度的影响进行对比如图11所示，图12所示是将图11在故障后(85h之后)的预测图形放大图。使用均方根误差、平均绝对误差、希尔不等系数和平均相对变动值作为网络的评价指标，计算结果如表3所示。通过对比可以说明使用未标记数据对剩余寿命预测的算法精度有一定的提升，随着未标记数据的增多，预测精度有所升高，且波动情况相对平缓。

表3

显然，本发明的上述实施例仅仅是为清楚地说明本发明所作的举例，而并非是对本发明的实施方式的限定，对于所属领域的普通技术人员来说，在上述说明的基础上还可以做出其它不同形式的变化或变动，这里无法对所有的实施方式予以穷举，凡是属于本发明的技术方案所引伸出的显而易见的变化或变动仍处于本发明的保护范围之列。