任意声矢量传感器阵列近场源ESPRIT参数估计方法与流程

本发明属于信号处理技术领域，尤其涉及一种声矢量传感器阵列的近场源频率、二维到达角和距离的估计方法。

背景技术：

确定声波的到达方向是声信号处理的一个重要应用，早期的声波测向采用的是仅能测量声压强度信息的声压传感器，随着矢量传感器技术的发展，利用声矢量传感器进行波达方向估计受到国内外诸多学者的关注。不同于无指向性的标量声压传感器，声矢量传感器由一个声压传感器和可选的三个空间轴向垂直的质点振速传感器构成，正是由于这种特殊结构，声矢量传感器具备空间同步、共点测量声场中的标量声压信息和矢量振速信息的能力，因而能获得比传统声压传感器更多的信息量，从而使得声矢量传感器阵列能够获得比声压传感器阵列更好的定位精度和空间分辨率。

传统的声矢量传感器信号处理采用的是长矢量信号模型，该模型下的每一个声矢量传感器输出数据是用一个复数矢量来描述，声矢量传感器阵列中的多个输出数据顺序排列构成复数数据矢量。基于长矢量模型的数据处理并没有利用声矢量传感器各个分量间的正交关系，本发明利用声矢量传感器自身具有的正交矢量特性，构建了由x轴、y轴和z轴三个振速传感器分量和一个声压传感器分量组成的声矢量传感器的四元数新模型。因为近场的波面是球面波。阵元间的相位不仅与阵元间距有关而且与声源到阵元的距离有关，所以远场条件下具有的平移不变结构对于近场不再适用，标量传感器阵列无法利用旋转不变技术估计信号参数(esprit)方法估计近场声源信号的参数，现有的文献亦未涉及声矢量传感器阵列的近场源esprit参数估计方法，本发明利用声矢量传感器自身具有的旋转不变结构进行参数估计，进而给出了一种近场的声矢量传感器阵列参数估计esprit方法。

技术实现要素：

本发明的目的是提供一种近场源任意空间结构的声矢量传感器阵列esprit多参数估计方法。

为了实现上述目的，本发明采取如下的技术解决方案：

任意声矢量传感器阵列近场源esprit参数估计方法，k个不同频率、互不相关窄带、随机平稳近场声源信号从不同的方向和距离(θk，φk，rk)入射到该接收阵列，所述阵列由m个空间任意分布的阵元构成，所述阵元是具有同步共点测量声压以及x轴、y轴和z轴方向振速分量的声矢量传感器，所有传感器的对应通道相互平行：所有的声压传感器相互平行，所有的x轴方向振速传感器相互平行，所有的y轴方向振速传感器相互平行，以及所有的z轴方向振速传感器相互平行；相邻阵元间隔与入射声波信号的波长和声源的距离之间满足近场条件；

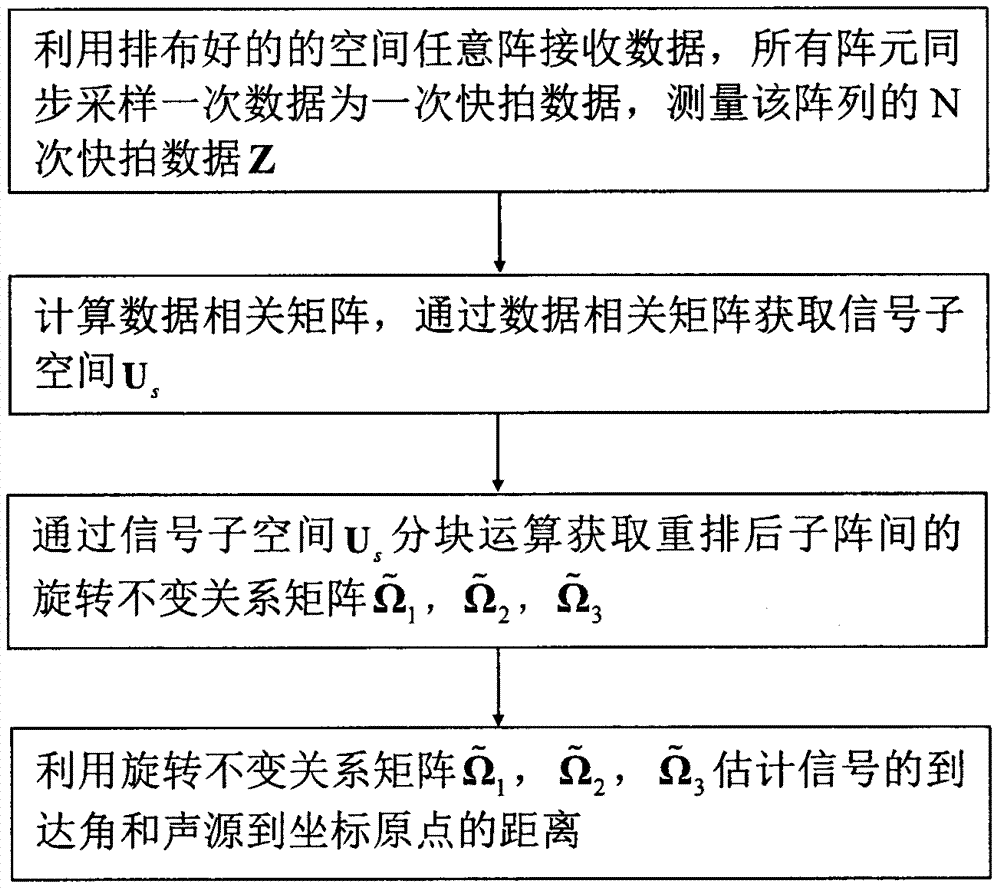
任意声矢量传感器阵列近场源esprit参数估计方法的步骤如下：

步骤一、m个空间任意分布的阵元构成空间任意阵接收近场信号，利用排布好的接收阵列获取数据，所有阵元同步采样一次的输出数据称为一次快拍数据，n次快拍数据构成阵列接收数据z；

步骤二、计算数据相关矩阵，由数据相关矩阵获取信号子空间us；

计算数据相关矩阵其中，e[·]表示求平均，[·]^h为矩阵的转置复共轭操作，rs＝e[ss^h]为入射信号相关矩阵，a＝[a1，…，ak，…，ak]是阵列导向矢量，

表示keroneck积，arctan(·)表示求反正切运算，θk∈[0，π/2]是第k个信号的俯仰角，φk∈[0，2π]是第k个信号的方位角，rk是第k个信号到坐标原点的距离，ρ0是环境流体密度，c是声波传播速度，λk是第k个声波信号的波长，i是4m×4m的单位矩阵，是高斯白噪声的功率，根据子空间理论对数据相关矩阵rz进行特征分解，k个大特征值对应的特征矢量构成信号子空间us，us是4m×k的矩阵，q(θk，φk，rk)为m个传感器与坐标原点的相位差构成的空域导向矢量；

步骤三、通过信号子空间us的分块运算获取重排后子阵间的旋转不变关系矩阵

根据数据排列方式将信号子空间us分成m×k的u1，u2，u3和u4四个子空间，即us＝[u1，u2，u3，u4]^t，其中us＝at，u1＝a1t，u2＝a2t，u3＝a3t，u4＝a4t，a就是步骤二中的阵列导向矢量矩阵，a1是x轴方向振速分量采样数据阵列导向矢量矩阵，a2是y轴方向振速分量采样数据阵列导向矢量矩阵，a3是z轴方向振速分量采样数据阵列导向矢量矩阵，a4是声压分量采样数据阵列导向矢量矩阵，t是阵列导向矢量和信号子空间之间的k×k的非奇异变换矩阵，可以得到ψ1t1＝ω1t1，ψ2t2＝ω2t2，ψ3t3＝ω3t3，其中是矩阵u3的伪逆矩阵，a1＝a3ω1，a2＝a3ω2，a4＝a3ω3，ω1是a1和a3间的旋转不变关系矩阵，ω2是a2和a3间的旋转不变关系矩阵，ω3是a4和a3间的旋转不变关系矩阵，对ψ1，ψ2，ψ3分别进行特征分解，特征值构成ω1，ω2，ω3的估计特征矢量构成t1，t2，t3的估计声矢量传感器在空间上共点，所以各个子阵对应的空域导向矢量相同，即构成相同的空间，但它们的列矢量的排列顺序不同，根据同一个列矢量与自身转置复共轭相乘是最大的原则将按照的顺序进行重排，和分别表示矩阵和的第k列，表示矩阵的第l列，和的对角线元素分别按照和的顺序进行重排，重排后的旋转不变关系矩阵分别为

其中，是重排后的导向矢量矩阵a1和a3间的旋转不变关系矩阵估计值，是重排后的导向矢量矩阵a2和a3间的旋转不变关系矩阵估计值，是重排后的导向矢量矩阵a4和a3间的旋转不变关系矩阵估计值；

步骤四、利用旋转不变关系矩阵估计信号的到达角和声源到坐标原点的距离：

其中，和分别表示矩阵和的第k行第k列元素，arg(·)表示取幅角，tan(·)和arctan(·)分别表示求正切和反正切运算；

前述步骤中的k＝1，...，k，l＝1，...，k，j表示虚数单位。

本发明采用的任意阵型的阵列，阵列的阵元为由声压传感器和x轴、y轴及z轴方向的振速传感器构成的声矢量传感器，并且所有的声压传感器相互平行，所有的x轴方向振速传感器相互平行，所有的y轴方向振速传感器相互平行，所有的z轴方向振速传感器相互平行。

本发明利用声矢量传感器自身具有的正交矢量特性，给出了声矢量传感器二维到达角和距离的近场esprit估计方法，突破了现有线阵近场源参数估计方法只能估计一维到达角的局限性，解决了近场条件下声矢量传感器阵列不具有的平移不变结构，无法利用esprit方法的难题，该发明方法不限定阵列阵型，根据同一个列矢量与自身转置复共轭相乘是最大的原则进行参数配对。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中需要使用的附图做简单介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明实施例声矢量传感器阵列的示意图；

图2为本发明方法的流程图；

图3为本发明方法的到达角估计散布图；

图4为本发明方法的俯仰角估计均方根误差随信噪比的变化曲线图；

图5为本发明方法的方位角估计均方根误差随信噪比的变化曲线图；

图6为本发明方法的到达角估计均方根误差随信噪比的变化曲线图；

图7为本发明方法的距离估计均方根误差随信噪比的变化曲线图；

图8为本发明方法的到达角估计成功概率随信噪比的变化曲线图。

具体实施方式

为了让本发明的上述和其它目的、特征及优点能更明显，下文特举本发明实施例，并配合所附图示，做详细说明如下。

图1所示为本发明实施例的声矢量传感器阵列的示意图。本发明的声矢量传感器阵列由m个空间任意分布的阵元构成，所述阵元是具有同步共点测量声压以及x轴、y轴和z轴方向振速分量的声矢量传感器，阵元间隔与入射声波信号的波长和声源的距离之间满足近场条件；

参照图2，本发明的近场源esprit参数估计方法的步骤如下：任意阵型声矢量传感器阵列接收k个不同频率、互不相关窄带、随机平稳近场声源信号，k为入射声源信号的数量，

步骤一、m个空间任意分布的阵元构成空间任意阵接收近场信号，利用排布好的接收阵列获取数据，所有阵元同步采样一次的输出数据称为一次快拍数据，n次快拍数据构成阵列接收数据z；

步骤二、计算数据相关矩阵，由数据相关矩阵获取信号子空间us；

计算数据相关矩阵其中，e[·]表示求平均，[·]^h为矩阵的转置复共轭操作，rs＝e[ss^h]为入射信号相关矩阵，a＝[a1，…，ak，…，ak]是阵列导向矢量，

表示keroneck积，arctan(·)表示求反正切运算，θk∈[0，π/2]是第k个信号的俯仰角，φk∈[0，2π]是第k个信号的方位角，rk是第k个信号到坐标原点的距离，ρ0是环境流体密度，c是声波传播速度，λk是第k个声波信号的波长，i是4m×4m的单位矩阵，是高斯白噪声的功率，根据子空间理论对数据相关矩阵rz进行特征分解，k个大特征值对应的特征矢量构成信号子空间us，us是4m×k的矩阵，q(θk，φk，rk)为m个传感器与坐标原点的相位差构成的空域导向矢量；

步骤三、通过信号子空间us的分块运算获取重排后子阵间的旋转不变关系矩阵

根据数据排列方式将信号子空间us分成m×k的u1，u2，u3和u4四个子空间，即us＝[u1，u2，u3，u4]^t，其中us＝at，u1＝a1t，u2＝a2t，u3＝a3t，u4＝a4t，a就是步骤二中的阵列导向矢量矩阵，a1是x轴方向振速分量采样数据阵列导向矢量矩阵，a2是y轴方向振速分量采样数据阵列导向矢量矩阵，a3是z轴方向振速分量采样数据阵列导向矢量矩阵，a4是声压分量采样数据阵列导向矢量矩阵，t是阵列导向矢量和信号子空间之间的k×k的非奇异变换矩阵，可以得到ψ1t1＝ω1t1，ψ2t2＝ω2t2，ψ3t3＝ω3t3，其中是矩阵u3的伪逆矩阵，a1＝a3ω1，a2＝a3ω2，a4＝a3ω3，ω1是a1和a3间的旋转不变关系矩阵，ω2是a2和a3间的旋转不变关系矩阵，ω3是a4和a3间的旋转不变关系矩阵，对ψ1，ψ2，ψ3分别进行特征分解，特征值构成ω1，ω2，ω3的估计特征矢量构成t1，t2，t3的估计声矢量传感器在空间上共点，所以各个子阵对应的空域导向矢量相同，即构成相同的空间，但它们的列矢量的排列顺序不同，根据同一个列矢量与自身转置复共轭相乘是最大的原则将按照的顺序进行重排，和分别表示矩阵和的第k列，表示矩阵的第l列，和的对角线元素分别按照和的顺序进行重排，重排后的旋转不变关系矩阵分别为

其中，是重排后的导向矢量矩阵a1和a3间的旋转不变关系矩阵估计值，是重排后的导向矢量矩阵a2和a3间的旋转不变关系矩阵估计值，是重排后的导向矢量矩阵a4和a3间的旋转不变关系矩阵估计值；

步骤四、利用旋转不变关系矩阵估计信号的到达角和声源到坐标原点的距离：

其中，和分别表示矩阵和的第k行第k列元素，arg(·)表示取幅角，tan(·)和arctan(·)分别表示求正切和反正切运算；

前述步骤中的k＝1，...，k，l＝1，...，k，j表示虚数单位；

本发明给出了基于任意阵型的近场源参数估计的esprit方法，根据空间上共点的声矢量传感器的各个子阵对应的空域导向矢量相同的特点，利用同一个列矢量与自身转置复共轭相乘是最大的原则，对特征矢量和特征值重排，从而获取子阵间的旋转不变关系矩阵，利用旋转不变关系矩阵得到信号的到达角和声源到坐标原点的距离估计值，该方法突破了现有线阵参数估计方法的局限性以及多重信号分类(music)方法的全域三维搜索的超大计算量难题，参数配对运算简单；

本发明的效果可以通过以下的仿真结果进一步说明：

仿真实验条件如下：

不失一般性，假设两个不同频率、互不相关窄带、随机平稳近场声源信号入射到由9个阵元构成的空间任意排布的声矢量传感器阵列，各阵元坐标分别为(0.2λmin，0.2λmin，0)，(0.3λmin，0.2λmin，0)，(0.4λmin，0.3λmin，0)，(0.2λmin，0，0.2λmin)，(0.2λmin，0，0.4λmin)，(0.3λmin，0，0.5λmin)，(0，0.4λmin，0.4λmin)，(0，0.5λmin，0.5λmin)，(0，0.7λmin，0.2λmin)，λmin为入射声波信号的最小波长，如图1所示，入射信号的参数为：(θ1，φ1)＝(20°，24°)，(θ2，φ2)＝(50°，27°)，其归一化频率为(f1，f2)＝(0.3，0.4)，快拍数为512次，200次独立实验。

仿真实验结果如图3至图8所示，图3为信噪比是15db时，本发明方法到达角估计的散布图，从图3可以看出本发明方法可以估计出到达角参数，且本发明方法有较高的到达角参数估计精度；从图4和图7可以看出本发明方法，俯仰角、方位角、到达角和距离估计的均方根误差较小，也就是估计值在真值附近的较小范围内扰动；到达角估计成功概率是指在200次独立试验中俯仰角和方位角估计值满足关系式的实验次数占总实验次数的百分比；其中，θ0和φ0是真值，和是指第i次实验的估计值，从图8可以看出，本发明方法的成功概率很高，特别是0db时，本发明方法的成功概率已达到了80％以上；

以上所述，仅是本发明的较佳实施例而已，并非对本发明做任何形式上的限制，虽然本发明已以较佳实施例揭露如上，然而并非用以限定本发明，任何熟悉本专业的技术人员，在不脱离本发明技术方案范围内，当可利用上述揭示的技术内容做出些许更动或修饰为等同变化的等效实施例，但凡是未脱离本发明技术方案的内容，依据本发明的技术实质对以上实施例所作的任何简单修改、等同变化与修饰，均仍属于本发明技术方案的范围内。