基于GNSS的紫外敏感器系统误差在轨标定方法与流程

本发明涉及卫星导航技术领域，特别的，涉及一种基于gnss的紫外敏感器系统误差在轨标定方法。

背景技术：

目前的在轨卫星大多依赖地面设备获取导航信息，地面工作站的任务越来越繁重，人们对卫星的自主运行能力提出了越来越高的要求。作为自主运行能力之一，卫星的自主导航即是指卫星不依赖于地面设备支持，而是利用星上自备的有效载荷和测量设备实时地确定自身的位置和速度，是当今卫星控制技术发展的必然要求。高轨卫星(heo)一般指轨道高度在20000km以上的高地球轨道卫星。这类卫星具有更好的安全稳定性和更大的对地覆盖面积，因此相对于低轨卫星具有更加重要的意义，一般多为导航、通讯卫星和特殊军用卫星，在陆地和海洋通信、气象探测、教育应用、电视直播、灾难预警以及空间太阳能站等方面都有着很重要的用途。

全球导航卫星系统(globenavigationsatellitesystem,gnss)能提供全球、全天候、连续和高精度的导航定位服务，已广泛应用于陆地、海洋、航空航天等领域。高轨卫星一般运行于比gnss卫星更高的轨道上，因而只能接收到来自地球背面的间断gnss卫星信号，所以一般通过采取高灵敏度接收机，联合多个gnss星座，来增加可用gnss可用星数以提高星上自主定位的能力和精度。但是，由于gnss的可靠性不高，电磁波易被干扰破坏，因此需要其他方式的导航敏感器来增加高轨卫星定位的自主性。紫外敏感器在紫外波段能探测出整个天体的边缘，且其成像稳定可与红外成像媲美。作为天文导航设备之一，它具备可靠性高、隐蔽、无源、不易受电磁干扰等优点，能够利用地球等天体的紫外辐射特性获取卫星的姿态信息。因此，利用高灵敏度接收机，在gnss可用阶段能够利用gnss测量信息完成高轨卫星高精度定位，在gnss不可用阶段利用紫外敏感器获得的地心位置信息完成卫星自主导航的任务，是构建自主导航系统的有效途径之一，也是目前使用较广泛的一种导航方式(如中国专利201410106004.8提出的一种在轨飞行器自主导航系统，但该专利中并没有提及如何对系统的误差进行估计)。

紫外敏感器由于像点提取误差、主点偏差、焦距偏差、成像平面的倾斜与旋转以及镜头畸变等误差因素会造成x轴与y轴的像素偏差，从而造成航天器的导航误差，中国专利2010106238513公开了一种自主导航系统误差校正方法，该方案中仅利用紫外敏感器对地球的观测量及星敏感器对恒星的观测量进行滤波解算，其导航结果精度低(经本发明人仿真试验，其一维系统误差估计精度约为50％)，另外，该方案将系统误差扩展为系统状态量，通过滤波算法，对卫星位置、速度、系统误差一起进行估计，进而对紫外敏感器的系统误差进行补偿，由于需要对状态量进行扩展，滤波估计中的维数多，因此，计算步骤繁杂，工作量大，降低系统的响应速度。

技术实现要素：

本发明目的在于提供一种基于gnss的紫外敏感器系统误差在轨标定方法，以解决背景技术中提出的问题。

为实现上述目的，本发明提供了一种基于gnss的紫外敏感器误差在轨标定方法，包括以下步骤：

1)在gnss可用时，使高轨卫星上的星载接收机对gnss卫星进行观测，建立gnss伪距观测方程；使高轨卫星上的紫外线敏感器对地球进行观测，建立紫外敏感器观测方程；

2)利用步骤1得到的gnss测量信息得到高轨卫星位置信息，通过非线性滤波算法处理高轨卫星位置信息，得到gnss伪距测量信息下的高精度导航结果；

3)通过最小二乘法处理步骤1得到的紫外敏感器观测量与步骤2得到的高精度导航结果，得到紫外敏感器的误差估计值(即为系统误差估计值)；

4)以步骤3得到的紫外敏感器的误差估计值为标定值，在gnss不可用时对高轨卫星的导航信息进行补偿，从而提高导航精度。

进一步的，步骤1中，紫外敏感器的观测方程如式1所示：

其中，δx、δy分别为紫外光学敏感轴在像平面内由于像点提取误差、主点偏差、焦距偏差、成像平面的倾斜与旋转，以及镜头畸变等误差因素的影响造成的x轴和y轴的像素偏差；f为紫外敏感器的焦距；为紫外敏感器测量的地心惯性系下的高轨卫星质心位置矢量；为测量系到惯性系的转换矩阵，为紫外敏感器的测量量(即紫外敏感器获得的观测量)，εr为观测随机噪声。

步骤1中，gnss伪距观测方程如式2所示：

其中，下标j表示gnss卫星编号，ρj为伪距测量值(高轨卫星与gnss卫星之间的距离，即gnss的测量量)，为gnss卫星在信号发射时刻的地心惯性位置矢量，rⁱ为高轨卫星在信号接收时刻的地心惯性位置矢量，c为导航信号传播速度，δtj为gnss卫星钟差，δtr为高轨卫星上的接收机钟差，δρj,ion为电离层时延误差；为高轨卫星上的接收机伪距测量噪声。

进一步的，步骤2中，采用扩展卡尔曼滤波对gnss测量信息进行处理，具体步骤为：

2.1)建立式3的非线性离散系统：

其中，xk+1为高轨卫星在k+1时刻的状态量，zk+1为高轨卫星在k+1时刻的测量量，其包括紫外测量量和gnss测量量，h(xk+1)为观测方程，其包括式1与式2所表示的观测方程，f(xk)为高轨卫星的轨道动力学方程，wk、vk+1均为高斯白噪声，且互不相关，其统计特性如式4：

其中，qk为对称非负定矩阵，rk为对称正定矩阵，初始状态x0独立于wk、vk，其均值和协方差如式5：

2.2)初始化状态量和方差阵p0如式6-1与式6-2：

2.3)将状态方程和测量方程分别围绕该时刻(即k+1时刻)的滤波值展开成泰勒级数，并在附近线性化，可得式7与式8：

其中，t为滤波更新周期，为zk+1在附近进行一阶泰勒展开得到的线性化观测矩阵，为状态一步预测，即k时刻的状态xk只经过状态更新(即式7)得到的k+1时刻的状态

2.4)时间更新，具体如式9-1、式9-2与式10：

xk+1,k＝φk+1xk/k(式9-1)；

其中，

i为单位矩阵，φk+1为由式10得到的状态转移矩阵，为状态转移矩阵φk+1的转置，为过程噪声协方差阵，f(x)为高轨卫星的轨道动力学方程。

2.5)测量更新，具体如式11～式14：

状态量更新如式11：xk+1＝xk+1,k+kk+1(zk+1-h(xk+1,k))(式11)；

其中，kk+1为滤波增益，h(xk+1k)为由一步预测状态经观测方程得到的预测观测量；

滤波增益如式12：

其中，hk+1为观测矩阵，为观测矩阵hk+1的转置，pk+1,k为预测方差阵，rv,k+1为测量噪声协方差阵；

协方差阵更新如式13：pk+1＝(i-kk+1hk+1)pk+1,k(式13)；

其中，

h(x)包括式1与式2所示的观测方程；

2.6)利用式11和式13获得的状态量和方差阵返回扩展卡尔曼滤波器，用于下一时刻，经过一定的循环迭代次数，最终得到gnss伪距测量信息下的高精度导航结果

步骤3中用最小二乘法处理步骤1得到的紫外敏感器观测量与步骤2得到的高精度导航结果，具体为：

将步骤2中由gnss导航卫星解算出来的高轨卫星的位置矢量记为代入步骤1的紫外敏感器观测方程中，令为紫外敏感器的测量量，可以将等式转化为式15的形式：

y＝hθ(式8)；

其中

θ＝[δx,δy,0]^t(式11)；

系统误差的最小二乘估计如式19：

步骤4中，将由式19得到的系统误差估计值作为标定值，对系统的误差进行补偿，即可得到较高精度的导航信息。

有益效果：本发明提供了一种基于gnss的紫外敏感器系统误差在轨标定方法，在gnss可用时利用最小二乘法处理紫外敏感器测量量与gnss高精度定位结果，可较为准确地得到导航系统的系统误差估计值，用于在gnss不可用时对导航信息进行补偿，操作简单、适用范围广(也可适用于中低轨卫星的导航)，紫外敏感器的系统误差模型(即紫外敏感器的观测方程)改变后也能依据本发明的方法类推出紫外敏感器的系统误差，可扩展性强。

本发明在系统误差估计过程中，没有对状态量进行扩展，在滤波估计中，状态维数不再进行增加，维数的减少有利于增强滤波器的稳定性和加快滤波收敛速度，故本发明给出的系统误差估计方法能够较快地给出高精度的系统误差估计结果。

除了上面所描述的目的、特征和优点之外，本发明还有其它的目的、特征和优点。下面将参照图，对本发明作进一步详细的说明。

附图说明

构成本申请的一部分的附图用来提供对本发明的进一步理解，本发明的示意性实施例及其说明用于解释本发明，并不构成对本发明的不当限定。在附图中：

图1是本发明优选实施例的实施流程示意图；

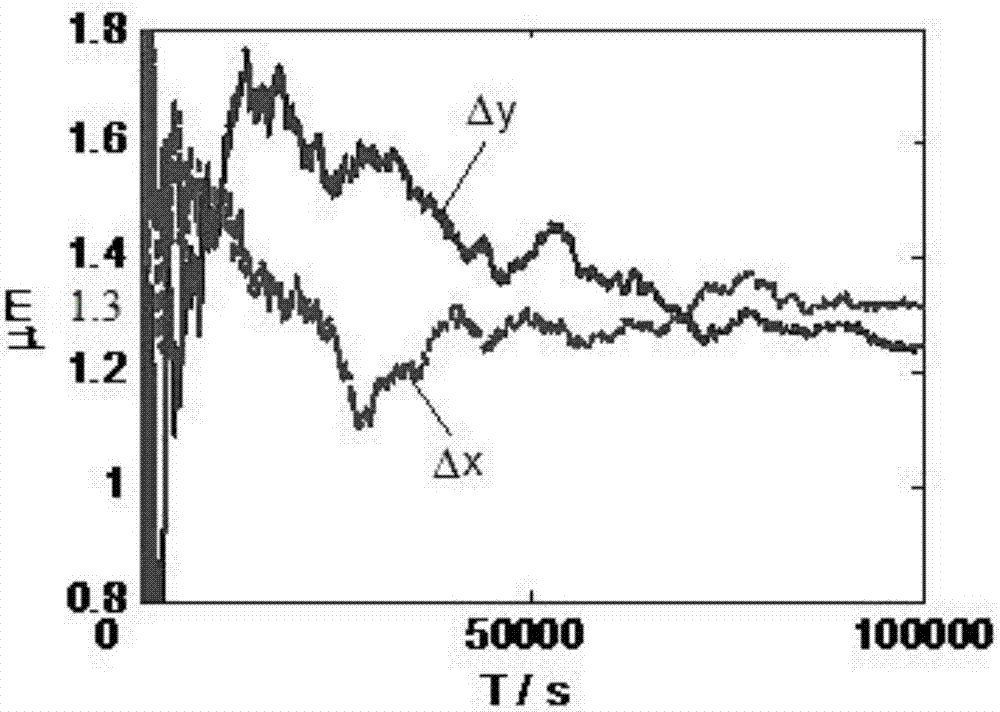
图2是本发明优选实施例的方法的误差估计效果对比图；

图3是利用本发明的优选实施例的方法对系统误差进行补偿后的导航效果对比图。

具体实施方式

以下结合附图对本发明的实施例进行详细说明，但是本发明可以根据权利要求限定和覆盖的多种不同方式实施。

如图1所示，一种基于gnss的紫外敏感器在轨标定方法，具体的实施步骤如下：

1)在j2000.0地心赤道坐标系中，仅考虑j2摄动，建立高轨卫星轨道动力学模型如式20：

式20中

rⁱ＝[x；y；z；](式14-1)；

vⁱ＝[vx；vy；vz；](式15-2)；

其中，rⁱ为地心惯性系下高轨卫星的位置矢量，r为高轨卫星距地心的距离，即vⁱ为地心惯性系下高轨卫星的速度矢量；gⁱ为地心惯性系下高轨卫星受到的摄动力矢量；μ为地球引力常数；re为地球半径；j2为二阶带谐项系数。

2)在gnss可用时，使高轨卫星上的星载接收机对gnss卫星进行观测，建立gnss伪距观测方程；

gnss伪距观测方程如式21：

其中，下标j表示gnss卫星编号，ρj伪距测量值，为卫星在信号发射时刻的地心惯性位置矢量，rⁱ为高轨卫星在信号接收时刻的地心惯性位置矢量，c为导航信号传播速度，δtj为gnss导航卫星钟差，δtr为接收机钟差，δρj,ion为电离层时延误差；为接收机伪距测量噪声。

使高轨卫星上的紫外线敏感器对地球进行观测，建立地心惯性系下的紫外敏感器导航观测方程；

紫外敏感器导航观测方程如式22：

δx、δy分别为紫外光学敏感轴在像平面内由于像点提取误差、主点偏差、焦距偏差、成像平面的倾斜与旋转，以及镜头畸变等误差因素的影响造成的x轴和y轴的像素偏差；f为紫外敏感器的焦距；为紫外敏感器测量的地心惯性系下的卫星质心位置矢量；εr为观测随机噪声。

3)利用gnss测量信息得到高轨卫星位置信息，主要有几何法和动力学法，以动力学为例，采用扩展卡尔曼滤波对gnss信息进行处理，具体如步骤3.1～3.6：

3.1)采用式23的非线性离散系统：

式中wk均为高斯白噪声，且互不相关，其统计特性如式24：

其中，qk为对称非负定矩阵，rk为对称正定矩阵。初始状态x0独立于wk、vk，其均值和协方差为：

3.2)初始化状态量和方差阵p0如式26-1与式26-2：

3.3)将状态方程和测量方程分别围绕该时刻的滤波值展开成泰勒级数，并在附近线性化，可得式27与式28：

3.4)时间更新，具体如式29-1、式29-2与式30：

xk+1,k＝φk+1xk/k(式29-1)；

其中，

3.5)测量更新，具体如式31～式34：

状态量更新：xk+1＝xk+1,k+kk+1(zk+1-h(xk+1,k))(式23)；

滤波增益：

协方差阵更新：pk+1＝(i-kk+1hk+1)pk+1,k(式25)；

式中：

3.6)利用获得的状态量和方差阵返回扩展卡尔曼滤波器，用于下一时刻，经过一定的循环迭代次数，最终得到gnss伪距测量信息下的高精度导航结果

4)用最小二乘法处理gnss高精度定位结果和紫外敏感器观测信息，得到系统误差估计值，具体步骤为：

将gnss导航卫星解算出来的高轨卫星的位置矢量记为假设使用联合gnss，并利用主旁瓣信号，保证可用卫星的数目，得到的高轨卫星位置矢量精度远高于紫外敏感器的定位精度，故将其假设为真实的高轨卫星位置矢量，代入式21的紫外敏感器测量方程中，令为紫外敏感器的测量量，可以将紫外敏感器的测量方程转化为式35的形式：

式35经过等价转换可得式36：

将式36转化为式37的形式：

y＝hθ(式29)

其中

θ＝[δx,δy,0]^t(式40)

故根据最小二乘算法可知系统误差的最优估计为：

5)以式41得到的系统误差估计值为标定值，在gnss不可用时对系统导航信息进行补偿，输出系统误差估计值及补偿后的高轨卫星的位置和速度信息，得到较高精度导航结果。

以某一地球高轨为例，初始轨道根数为：半长轴42000km，偏心率0.00003，轨道倾角5°，升交点赤经0°，近交点角距0°，平近点角276°；高轨卫星接收机灵敏度为-182dbw；紫外敏感器像素误差为1.3μm；导航时间为3天。

图2给出了本发明所提出的系统误差估计方法的估计结果(δx为式1中所示像平面内x轴方向的像素误差；δy为式1中所示像平面内y轴方向的像素误差)，可以看出估计结果接近1.3μm(由仿真系统设定的真实值)，x轴方向的像素误差为5％，y轴方向的像素误差为1％，准确度较高。

图3为是利用本发明优选实施例方法对系统误差进行补偿后的导航效果对比图(其中最上面的“无误差补偿”曲线指的是不对紫外敏感器的系统误差进行标定补偿得到的结果，最下面的“误差补偿”曲线指的是利用本实施例的方法对紫外敏感器的系统误差进行补偿后，得到的单次样本结果，中间的“误差补偿1σ”曲线为“误差补偿”单次样本结果对应的协方差值)，从图3可以看出，利用本发明提出的方法对紫外敏感器进行系统误差估计补偿后，导航精度从2km提高到1km左右，本发明的方法的有益效果得到验证。

以上所述仅为本发明的优选实施例而已，并不用于限制本发明，对于本领域的技术人员来说，本发明可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。