无源雷达目标跟踪方法与流程
本发明涉及雷达技术,特别涉及无源雷达目标跟踪技术。特别是跟踪区域存在多个目标、并且各个目标航迹会出现中断现象,致使跟踪滤波后的航迹呈不连续状态下的目标跟踪技术。
背景技术:
在无线电探测技术领域,无源雷达自身不用发射电磁波,通过接收目标辐射的电磁信息对目标进行定位和跟踪。无源雷达系统具有作用距离远、隐蔽性好等优点,对于提高系统在电子站环境下的生存能力具有重要作用。无源雷达系统是基于目标辐射的电磁波参数来确定辐射源以及其携载平台或目标位置信息的,系统的关键技术在于量测数据的处理并形成稳定航迹。无源雷达常用的数据处理方式类似于有源雷达,主要包含有数据预处理,数据关联,航迹起始,滤波跟踪,航迹终结,形成航迹等步骤。数据预处理解决系统误差配准、时间同步、空间对准及野值剔除等问题。航迹起始与终结是目标运动在雷达观测区域下的航迹建立和航迹结束的过程,尤其航迹起始是雷达数据处理的重要过程,决定能否对目标实现跟踪。数据关联和滤波跟踪解决量测点迹与目标的关联,以及通过量测值对目标状态的估计等问题。形成航迹是将同一目标的量测集合所估计的目标状态形成同一航迹的过程。
对于无源雷达系统预处理(时间同步、野值剔除)后的方位角量测集合进行定位跟踪,由于空间中量测方位角与目标位置具有很强的非线性关系,所以采用不敏卡尔曼滤波器(unscentedkalmanfilter,ukf)进行滤波。对于机动目标的跟踪,采用交互式多模型(interactingmultiplemodelalgorithm,imm)的自适应算法进行跟踪。对于多个目标的数据关联,采用联合概率数据互联算法(jointprobabilisticdataassociationalgorithm,jpda)来解决杂波环境下的多目标互联问题,以及回波落入多个跟踪相关波门的相交区域的数据关联问题。对机动目标跟踪,可以将交互式多模型(imm)算法和不敏卡尔曼滤波(ukf)算法相结合,即将imm算法中的滤波器用ukf滤波器替换,得到imm_ukf算法。此方法可以解决无源雷达中的跟踪问题,可以有效检测目标运动的机动性,可以提高目标跟踪的状态估计。
通过这些基础处理方法基本可以对量测点集合形成稳定航迹。然而由于无源雷达自身不发射探测信号的固有特质,当辐射源目标不再辐射信号或者地面障碍物遮挡等情况造成目标量测数据不连续,使得采用上述方法对同一目标形成的航迹出现间断现象,尤其当复杂环境下当多个目标同时出现间断,将给目标形成同一稳定航迹带来困难。
技术实现要素:
本发明的目的提供计一种无源雷达多目标跟踪方法,不仅可以对不间断的连续量测数据进行关联形成稳定航迹,也可以对阈值时间内有部分丢失的量测数据(即出现航迹中断现象)进行关联,可以对同一批多目标中的每个目标都形成与之对应的一条稳定航迹。以克服现有技术只能对目标的连续采样量测数据形成稳定航迹,不能对同一目标前后时间有中断现象的量测数据形成同一航迹的问题。
本发明解决所述技术问题,采用的技术方案是,无源雷达目标跟踪方法,包括如下步骤:
a、跟踪预处理:根据雷达站达采集的方位角量测集合z(k)进行交叉定位,得到与定位目标关联的量测集合u(k);根据定位结果使用速度、加速度、角度约束进行航迹起始,并获得目标的初始状态估计和对应的协方差矩阵估计;
b、航迹跟踪滤波:对满足起始航迹的目标进行目标跟踪获得目标各个时刻的航迹及状态估计;
c、中断航迹预处理:对中断时刻前的旧航迹按中断时刻的多模型概率进行预测得到该目标航迹中断后tth+tsm时间内的旧航迹预测状态估计,其中tth是新、旧航迹间隔的最大时间,tsm是序贯关联时间窗长度;
d、中断航迹序贯关联:根据航迹中断时刻航迹中断的目标个数n,以及航迹中断后tth+tsm时间内新起始航迹目标个数m,初始化关联检验矩阵ψn×m;对每个旧航迹的目标预测状态估计与新航迹逆向状态估计在序贯关联窗长度tsm内进行序贯法关联得到检验矩阵ψn×m;再次按照每个旧航迹最多存在一条新航迹与之对应关联、每条新航迹最多存在一条旧航迹与之关联的约束准则和置信度水平α下的检验门限γ1-α对检验矩阵ψn×m进行处理,得到最后的关联确认矩阵ωn×m;
e、航迹确认:按照关联确认矩阵ωn×m的关联结果,对关联成功的新航迹赋以旧航迹的航迹号,并以中断时间内的旧航迹的状态预测值代替该目标中断时间段内目标状态估计值;其余新航迹的航迹号不变,并标识为新目标出现;对未关联成功的旧航迹以航迹终结处理。
具体的:步骤b具体为,对满足起始航迹的量测采用imm_ukf和jpda算法进行目标跟踪获得目标各个时刻的航迹及状态估计。
具体的:选取tsm为采样时间ts的3~5倍。
进一步的:步骤c还包括,对中断时刻后tth+tsm时间内出现的新目标按时间逆向进行滤波得到其航迹开始的tsm时间内的新航迹状态估计。
具体的:所述雷达站包括不在同一位置的至少3个移动和/或固定雷达站。
具体的:所述雷达站位于同一平面上。
具体的:所述雷达站数量为3个。
进一步的:所述3个雷达站中,其中一个雷达站处于另外两个雷达站连接线的垂直平分线上。
具体的:
z(k)={z1(k),z2(k),z3(k)}
式中zs(k)是k时刻第s个雷达站的方位角量测集合,且满足
其中
具体的:步骤a中,所述交叉定位是根据方位角量测集合z(k)解算出所有时刻内所有目标的位置坐标。
本发明根据多站无源雷达的方向角信息进行定位,使用速度、加速度、角度约束的直观法进行航迹起始;使用imm算法对机动目标进行跟踪,使用ukf算法解决跟踪系统非线性问题,使用jpda方法解决多目标关联问题,从而获得目标航迹及目标状态估计。然后对某量测中断航迹进行预测,对中断时间后tth+tsm时间内的新航迹进行反向估计,接着使用序贯关联方法关联新旧航迹并得到检验矩阵ψn×m,然后再对ψn×m进行约束处理求解最优航迹关联的关联确认矩阵ωn×m。本发明不仅可以对无源雷达多目标进行定位跟踪,提高航迹起始时间内的目标估计精度,同时也可以解决阈值时间内的中断航迹关联问题。克服了现有技术只能对目标的连续采样量测数据形成稳定航迹,不能对同一目标前后时间有中断现象的量测数据形成同一航迹的缺陷。
下面结合附图和具体实施方式对本发明做进一步的说明。本发明附加的方面和优点将在下面的描述中部分给出,部分将从下面的描述中变得明显,或通过本发明的实践了解到。
附图说明
构成本申请的一部分的附图用来提供对本发明的进一步理解,本发明的具体实施方式、示意性实施例及其说明用于解释本发明,并不构成对本发明的不当限定。在附图中:
图1是跟踪单个目标的n个模型的imm_ukf算法的示意图,图中包含n个模型,图中滤波器采用ukf滤波器。图中的
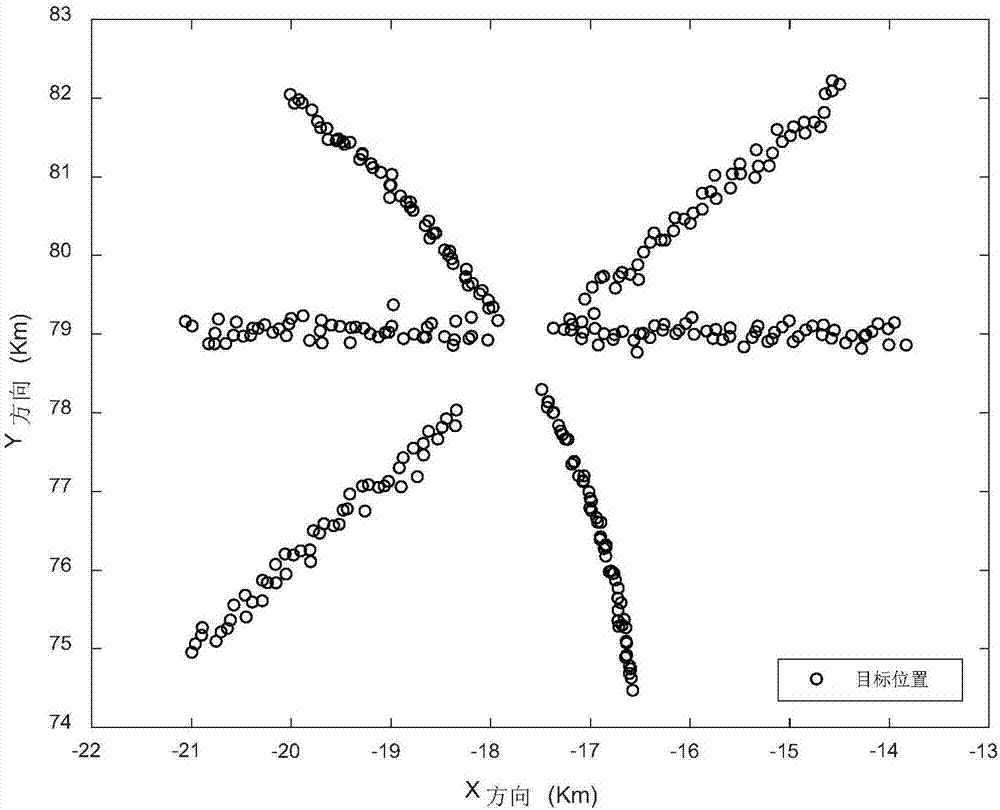
图2是本发明具体实施方式中三个目标120秒内的量测位置,图中圆圈表示某目标某时刻在空间中的位置坐标。
图3是图2中量测数据经过发明中的a、b步骤后跟踪到的6段航迹,图中包含有量测点迹,旧航迹1、旧航迹2、旧航迹3、新航迹1、新航迹2、新航迹3。
图4是经过中断航迹预测得到的结果,图中包含有量测点迹,旧航迹1、旧航迹2、旧航迹3、旧航迹预测航迹1、旧航迹预测航迹2、旧航迹预测航迹3、以及三条新航迹的方向滤波航迹。
图5是图4的局部放大图。
图6是经过步骤d、e后得到的三个目标的最终航迹。
具体实施方式
需要说明的是,在不冲突的情况下,本申请中的具体实施方式、实施例以及其中的特征可以相互组合。现将参考附图并结合以下内容详细说明本发明。
为了使本领域技术人员更好的理解本发明方案,下面将结合本发明具体实施方式、实施例中的附图,对本发明具体实施方式、实施例中的技术方案进行清楚、完整的描述,显然,所描述的实施例仅仅是本发明一分部的实施例,而不是全部的实施例。基于本发明中的具体实施方式、实施例,本领域普通技术人员在没有做出创造性劳动的前提下所获得的所有其他实施方式、实施例,都应当属于本发明保护的范围。
本发明的技术方案,首先对无源雷达得到的方位量测集合使用视线交叉定位法、imm、jpda、ukf等算法对连续量测按照跟踪预处理、航迹跟踪滤波等步骤形成连续量测的稳定航迹以及估计出各个目标所对应的状态。其次在顺序时间范围内,当航迹终结时刻存在多个目标航迹(称为“旧航迹1,旧航迹2,旧航迹3,…”)终结,并在阈值时间范围出现一个或多个目标航迹(称为“新航迹1,新航迹2,新航迹3,…”)起始,将旧航迹预测航迹与新航迹逆向滤波航迹进行序贯关联形成关联检验矩阵,并对关联检验矩阵按约束条件处理,得到旧航迹与新航迹的关联确认矩阵,其中包含旧航迹与新航迹的关联配对信息,对关联成功的旧航迹用状态预测值和航迹预测值替代中断时间内的目标状态和航迹,并与新航迹组成稳定航迹,对未关联成功的旧航迹进行航迹终结处理,对未关联成功的新航迹当做新目标出现进行处理,对超出阈值范围时间的新航迹同样认为是新目标的出现。本发明的无源雷达目标跟踪方法,不但适用于固定雷达站进行目标跟踪,同样适用于移动雷达站进行目标盖章。本发明主要步骤如下:
跟踪预处理步骤:根据雷达站达采集的方位角量测集合z(k)进行交叉定位,得到与定位目标关联的量测集合u(k);根据定位结果使用速度、加速度、角度约束进行航迹起始,并获得目标的初始状态估计和对应的协方差矩阵估计。
航迹跟踪滤波:对满足起始航迹的目标采用imm_ukf和jpda算法进行目标跟踪获得目标各个时刻的航迹及状态估计。
中断航迹预处理步骤:对中断时刻前的旧航迹按中断时刻的多模型概率进行预测得到该目标航迹中断后tth+tsm时间内的旧航迹预测状态估计,其中tth是新、旧航迹间隔的最大时间,tsm是序贯关联时间窗长度。同时对中断时刻后tth+tsm时间内出现的新目标按时间逆向进行滤波得到其航迹开始的tsm时间内的新航迹状态估计。这里通常选取tsm为系统采样时间ts的3~5倍。
中断航迹序贯关联步骤:根据航迹中断时刻航迹中断的目标个数n,以及航迹中断后tth+tsm时间内新起始航迹目标个数m,初始化关联检验矩阵ψn×m;对每个旧航迹的目标预测状态估计与新航迹逆向状态估计在序贯关联窗长度tsm内进行序贯法关联得到检验矩阵ψn×m;再次按照每个旧航迹最多存在一条新航迹与之对应关联、每条新航迹最多存在一条旧航迹与之关联的约束准则和置信度水平α下的检验门限γ1-α对检验矩阵ψn×m进行处理,得到最后的关联确认矩阵ωn×m。
航迹确认步骤:按照关联确认矩阵ωn×m的关联结果,对关联成功的新航迹赋以旧航迹的航迹号,并以中断时间内的旧航迹的状态预测值代替该目标中断时间段内目标状态估计值;其余新航迹的航迹号不变,并标识为新目标出现;对未关联成功的旧航迹以航迹终结处理。
这里对上述步骤做以下补充说明:
1)、上述跟踪预处理步骤中,以位于同一平面的3个雷达站的方位角量测集合z(k)进行交叉定位。即
z(k)={z1(k),z2(k),z3(k)}(1)
式中zs(k)是k时刻第s个雷达站的方位角量测集合,且满足
其中
上述交叉定位就是根据方位角量测集合z(k)解算出所有时刻内所有目标的位置坐标,其过程如下:选取k时刻方位角量测,将s1、s2两个雷达站k时刻的方位角量测数据进行视线交叉定位得到多目标的可能分布总集合t(k),其中
式中ti(k)是m(k)个目标的第i种可能分布情况;
计算雷达站s3对ti(k)中的第m个目标的方位角量测估计值
式中m=1,2,...,min({ns1,ns2});is3=1,2,...,ns3且ns3≤m(k);α表示概率调节系数,根据测量误差取值,一般取雷达站量测误差标准差的3~5倍。进而求得t(k)中每个可能分布情况与s3雷达站的ns3个方位角量测关联的最大似然概率
其中
并由
ut(k)={βs1,m1,βs2,m2,βs3,m3}(10)
其中ut(k)是k时刻目标t的三个站的量测组成的方位角量测向量;且m1∈{1,2,...,ns1},m2∈{1,2,...,ns2},m3∈{1,2,...,ns3}。并根据ut(k)中任意两两组合并与相应的雷达站位置计算目标的三个位置估计
其中xt(k)=[xt(k),yt(k)]′表示k时刻目标t的位置坐标。k时刻目标位置集合可记为
对于连续三个时刻目标关联位置集合x(k)、x(k+1)、x(k+2),得到相应时刻的目标位置估计从三个集合中分别各取一个目标可以得到一个组合航迹,按时间顺序求得每个组合对应目标的速度,加速度,以及速度矢量夹角,再与事先约定条件:速度约束、加速度约束、角度约束等条件判断对应组合航迹是否为目标航迹来进行航迹起始。对组合航迹满足约束条件的,确认航迹起始并进行后续处理步骤。
2)、上述航迹跟踪滤波中,imm_ukf算法的示意图如图1所示,图1所示是跟踪一个目标时imm_ukf算法流程,对多个目标的跟踪时,对每个目标重复使用该算法即可,图中包含n个模型,图中滤波器采用ukf滤波器。图中的
用uk-1(j)表示模型j的概率,且uk-1(j)是模型概率向量uk中的第个j元素,则交互计算后n个滤波器在k时刻的输入如下
式中
式中,
假设模型j离散时间的系统方程为
x(k+1)=fj[k,x(k)]+vj(k)(17)
模型j离散时间的系统量测方程为
z(k)=hj[k,x(k)]+wj(k)(18)
将
式中上标m表示状态更新中的权值;上标c表示协方差更新中的权值;κukf、αukfβukf是ukf算法参数。
根据系统状态方程δ采样点的一步预测δ点
式中,
则目标的量测预测和相应的协方差为
式中,
式中,
得到滤波器输出
式中
再更新模型j的概率为
最后得到k时刻imm算法的交互式输出为
3)、上述航迹跟踪滤波中的jpda算法即是将方位角量测和目标跟踪航迹关联的算法,主要过程为:假设k时刻有t个目标,并有j个方位角量测落入相应的回波波门内。计算方位角量测j与目标t的关联似然概率βj,t,得到关联似然矩阵bj×t,则
式中
式中st(k)表示k时刻目标t的新息协方差,vj(k)表示方位角量测j对应的新息,且满足
式中,
建立一个j×t维的确认关联矩阵wj×t,并初始化其元素ωjt为0。求bj×t矩阵最大元素所对应的行列值,并将wj×t中对应行列的元素赋值为1;将bj×t中对应行列的所有元素赋值为0。一直重复该步骤,直到bj×t中所有元素都为0,得到最终的确认关联矩阵wj×t,其中ωjt为1的表示目标t和方位角量测j关联。
4)、上述中断航迹预处理中,对间断时刻之前的目标旧航迹按中断时刻的多模型概率进行预测该目标航迹终结后tth+tsm时间内的旧航迹预测状态估计的方法是:假设目标n中断时刻为kn,计算目标的预测状态估计和对应的估计协方差矩阵
其中
对km时刻出现的新的新目标m,并假设其在航迹出现的时间为km~(km+lm),则lmts是该目标出现总时间长度。对新目标m的逆向滤波过程为:将正常滤波过程中,所用的系统状态方程改为如下即可,
xm,逆(k-1|k)=f-1(k)xm,逆(k|k)+v(k)(42)
其中f(k)是正常系统的状态转移矩阵。其他处理过程和航迹跟踪滤波处理的过程类似,且不用考虑jpda算法。
5)、上述中断航迹序贯关联中,对旧航迹与新航迹的序贯关联法是将根据旧航迹
式中km的取值范围为0,1,2,...,tsm/ts。则检验量
其服从
再由根据每个旧航迹最多存在一条新航迹与之对应关联、每条新航迹最多存在一条旧航迹与之关联的约束条件、置信度水平α下的检验门限γ1-α、以及检验量矩阵ψn×m得到航迹关联确认矩阵ωn×m。其中检验量
公式(48)表示检验量
式中ωn,m是ωn×m中的元素。
实施例
本实施例的无源雷达目标跟踪方法,假设无源雷达跟踪系统是二维平面上的三站固定站跟踪系统(即系统包括3个相距一定距离,处于同一平面上的固定雷达站),并采用matlab软件进行仿真。
设三个雷达站的位置坐标分别为o1(-20km,0)、o2(20km,0)、o3(0,20km),并设三个站之间方位角量测互相独立,方位角量测误差均值为0,标准差都为σβ=0.02°,且服从高斯分布。
假定该系统采样间隔ts=1s,tth=22s,tsm=3s,仿真总时间t=120s。
设观测范围内有三个目标:目标t1在0~120秒内做匀速运动,其初始位置为xt1(-21km,75km),其初始速度vt1(55m/s,60m/s);目标t2在0~120秒内做匀速圆周运动,其初始位置为xt2(-20km,82km),其初始速度vt2(50m/s,-50m/s),角速度为
设雷达站的天线指向均为y轴正方向,且k时刻雷达站j的位置为
式中dβ是方位角测量误差,且其协方差为
设imm_ukf算法中含有一个匀速运动模型的过程噪声协方差qcv=1.8∧2i,六个转弯运动转弯速率为
设ukf算的参数为:αukf=0.01、βukf=2、κukf=0。
由上述仿真条件,可以得知仿真时间120秒内,三个站每个时刻的方位角量测数目同样多,则:
1)、跟踪预处理:处理每个时刻的三个雷达站的方位角量测,假设对k时刻的三个站的方位角量测,先选取k时刻的o1和o2两个站的方位角量测根据公式(52)计算得到视线交叉点
式中io1,io2∈{1,2,3};
假设一个目标与一个方位角量测一一对应,则得到可能分布总集合t(k),则
其中
再求ti(k)中三个目标在o3雷达站下的观测值
式中m,is3∈{1,2,3}。进一步得到三个目标分布情况ti(k)与o3雷达站真实方位角量测的关联概率为
式中
再求取最大
根据ut(k)计算目标t的位置估计zt(k)=[xt(k),yt(k)]′,其中t的取值为1、2、3;则
式中
画出所有目标所有时刻的位置估计图如图2所示;
同时可以计算目标t测量误差在直角坐标系下的协方差误差为
所以根据前两个时刻的方位角量测值得到目标t的初始状态估计和估计协方差为
2)、航迹跟踪滤波:根据跟踪预处理得到所有目标的初始状态估计和估计协方差,即公式(62)和公式(63),带入到imm_ukf算法中对所有进行跟踪滤波;
首先根据目标t在k-1时刻的状态估计
再根据公式(35)到公式(38)得到关联似然矩阵bj×t,建立确认关联矩阵wj×t,并初始化其元素ωjt为0。求bj×t矩阵最大元素所对应的行列值,并将wj×t中对应行列的元素赋值为1;将bj×t中对应行列的所有元素赋值为0。一直重复该步骤,直到bj×t中所有元素都为0,得到最终的确认关联矩阵wj×t;
根据wj×t的关联结果,将与目标t与之关联的方位角量测zt(k)带入到公式(27)到公式(34)得到所有目标t在k时刻的状态估计
若某个时刻ke起连续3个ts周期内没有方位角量测与目标t关联成功,则目标在ke时刻航迹中断;
若某个时刻ks有方位角量测未与所有ks-1时刻的目标关联成功,则认为是新目标出现,对于新目标的航迹跟踪滤波,则按照该目标ks时刻和ks+1时刻的方位角量测,按照上述跟踪预处理中公式(58)至公式(63)的处理方式得到
再利用航迹跟踪处理过程对其进行滤波;
最终得到经过航迹跟踪处理后的实施案例中三个目标的航迹如图3所示;
3)、中断航迹预处理:按顺序时间搜索出现所有目标出现航迹中断的所有时刻,并对所有中断按如下航迹中断预处理进行处理:
假设在中断时刻ke出现有n个旧目标中断,在ke之后阈值时间tth+tsm内又有m个新目标航迹出现;
设旧目标n出现航迹中断时刻为kn=ke,根据公式(39)至公式(41)得到所有n个旧目标在tth+tsm时间内的状态预测值和预测协方差,其中
设新目标m在出现的时刻为km航迹总长度为lmts,依据上述航迹跟踪处理中得到的新目标m在km+lm时刻的估计状态
至此得到各个中断航迹的预测值和新航迹的逆向估计如图4所示,其局部放大如图5所示;
4)、中断航迹序贯关联:上述中断航迹预处理结果,即得到的新航迹逆向状态估计
5)、航迹确认:上述中断航迹关联结果,得到关联确认矩阵ωn×m,根据ωn×m将有新航迹关联的旧航迹中断时间内的状态用状态预测值代替,并和新航迹形成稳定航迹;对未与新航迹关联的旧航迹确认航迹终结;对未与旧航迹确认关联的新航迹按新目标起始航迹;最终得到仿真结果如图6所示。
- 还没有人留言评论。精彩留言会获得点赞!