一种获取致密油藏岩心的液体渗透率的方法及装置与流程

本发明涉及致密油藏技术领域，特别涉及一种获取致密油藏岩心的液体渗透率的方法及装置。

背景技术：

致密油藏是当前全球非常规石油发展的亮点领域，是未来非常规石油发展的潜在资源。中国致密油分布范围广，类型多样，也呈现良好的勘探开发形势，初步预测中国致密油技术可采资源量为20×10⁸～25×10⁸吨。致密油形成机理、富集规律与常规油气藏不同，现有理论与技术方法已不能有效支撑致密油进一步扩大勘探成果，迫切需要通过对流体在微纳米孔隙渗流机理及致密油藏流体渗透率的计算方法等关键问题研究，为致密油的有效开发提供理论指导与技术保障。

致密油藏液体渗透率的准确获取对油藏开发方案制定、开发效果预测及油藏管理具有重要意义。致密油藏储层由于孔喉细小、孔隙结构复杂以及孔隙内表面积大，液体与孔隙界面相互作用显著且不可忽略，液体分子紧密吸附在固体表面并有序排列在其周围，构成具有一定强度和厚度的且不流动的液体边界层，可以减少液体流动半径，降低致密油藏液体渗透率。且液体边界层随孔喉半径、驱替压力、流体粘度的变化而发生变化，准确计算和测量致密油藏岩心液体渗透率十分困难。

目前表征致密油藏岩心液体渗透率主要有室内实验和模型计算两种方法。室内实验通过地下取芯井获得真实致密油藏天然岩心，通过室内流体驱替实验，并结合达西定律测量岩心液体渗透率。然而这种方法有以下几点不足。第一，致密油藏岩心取芯成本高，能获取的天然岩心数量少，如果每块岩心都开展岩心驱替实验费用巨大；第二，由于致密岩心渗透率极低，驱替实验达到驱替平衡时间长，且实验得到的液体渗透率误差较大；第三，由于驱替实验岩心数目少，很难准确得到不同孔喉结构的致密岩心液体渗透率变化的规律，拟合得到的不同孔喉结构岩心液体渗透率计算公式精度不高；第四，致密油藏岩心具有明显的非达西渗流特征，随着驱替压力梯度的变化，液体边界层的厚度发生变化，继而液体渗透率发生变化。因此，不同驱替压力下得到的液体渗透率不同，目前的实验通常只测定单一压力梯度下的液体渗透率，由于实验时间长，且测量精度不高，不同驱替压力下液体渗透率实验很少开展，因此不能准确描述致密油藏岩心液体渗透率随驱替压力变化而发生变化的规律。

第二种模型计算方法目前主要有两种计算模型。第一种计算模型是利用毛管束模型，结合边界层理论，利用恒速压汞方法描述喉道分布特征，建立了一种计算岩心液体渗透率的方法。但恒速压汞价格较为昂贵，且喉道分布用公式拟合，拟合公式以及参数a、b没有明确的物理意义，如果对不同的岩性都要做测试来求取这两个参数的值，耗时时间长；且没有考虑边界层厚度随驱替压力梯度的变化对液体渗透率的影响。第二种计算模型基于孔隙正太分布的假设，并基于边界层厚度公式，建立了一种致密油藏液体渗透率的方法。但真实岩心孔隙不符合正太分布，得到的液体渗透率计算公式复杂，不具有普遍适用性。

技术实现要素：

为解决现有技术的问题，本发明提出一种获取致密油藏岩心的液体渗透率的方法及装置，本技术方案有效的表征液体边界层厚度随驱替压力梯度的变化情况，继而准确计算驱替压力梯度下致密油藏岩心液体渗透率。

为实现上述目的，本发明提供了一种获取致密油藏岩心的液体渗透率的方法，包括：

构建具有孔隙分形特征和毛细管束迂曲度分形特征且考虑液体边界层分布的迂曲毛细管束模型，获取致密油藏岩心，并得到所述致密油藏岩心的孔隙度φ；

对所述致密油藏岩心进行压汞测试，获得岩心压汞曲线；

根据所述岩心压汞曲线确定最大孔隙半径rmax、最小孔隙半径rmin、平均孔隙半径

由压汞曲线对不同孔隙半径下孔隙数目的累积求和，然后同时取毛细管束累计数量n与孔隙半径r的对数，做二者的关系曲线，直线的斜率的绝对值即孔隙分形维数df；利用所述致密油藏岩心的孔隙度φ确定平均迂曲度τav，根据所述致密油藏岩心的孔隙度φ、孔隙分形维数df、最大孔隙半径rmax确定毛细管束模型的特征长度l0；利用所述毛细管束模型的特征长度l0获得毛细管束模型的横截面积a；根据平均迂曲度τav、所述毛细管束模型的特征长度l0、平均孔隙半径确定毛细管束模型的平均迂曲度分形维数dt；

确定不同孔隙半径r和不同压力梯度δp下的边界层厚度h；

根据最大孔隙半径rmax、最小孔隙半径rmin、孔隙分形维数df、毛细管束模型的平均迂曲度分形维数dt、边界层厚度h、毛细管束模型的特征长度l0、毛细管束模型的横截面积a确定具有分形特征且考虑液体边界层分布的迂曲毛细管束模型的致密油藏岩心液体渗透率。

优选地，所述具有孔隙分形特征和毛细管束迂曲度分形特征且考虑液体边界层分布的迂曲毛细管束模型由一系列不同半径和不同迂曲度的毛细管束组成；其中，孔隙分形特征通过孔隙分形维数df表示；毛细管束迂曲度分形特征通过毛细管束模型的平均迂曲度分形维数dt表示；毛细管束具有分形特征，满足分形关系为：式中：lt(r)为流体路径的实际长度,μm；l0为毛细管束模型的特征长度；dt为毛细管束模型的平均迂曲度分形维数；r为孔隙半径；

每根毛管束考虑了固液吸附形成的不动液体边界层，边界层的厚度h与毛细管束模型中的迂曲毛管束半径，流体粘度μ、驱替压力梯度δp有关，满足表达式：

其中，毛细管束模型中的迂曲毛管束半径与孔隙半径r等价。

优选地，还包括：

根据所述具有孔隙分形特征和毛细管束迂曲度分形特征且考虑液体边界层分布的迂曲毛细管束模型致密油藏岩心液体渗透率确定液体渗透率随驱替压力梯度变化规律。

优选地，所述具有分形特征且考虑液体边界层分布的迂曲毛细管束模型的致密油藏岩心液体渗透率的表达式为：

式中，φ表示致密油藏岩心的孔隙度；β1、β2、β3均为流体参数，β1、β2、β3随流体类型的变化而变化；δp为驱替压力梯度，mpa/m；μ为流体粘度，mpa·s。

为实现上述目的，本发明还提供了一种获取致密油藏岩心的液体渗透率的装置，包括：

模型构建单元，用于构建具有孔隙分形特征和毛细管束迂曲度分形特征且考虑液体边界层分布的迂曲毛细管束模型，获取致密油藏岩心，并得到所述致密油藏岩心的孔隙度φ；

岩心压汞曲线获取单元，用于对所述致密油藏岩心进行压汞测试，获得岩心压汞曲线；

第一参数确定单元，用于根据所述岩心压汞曲线确定最大孔隙半径rmax、最小孔隙半径rmin、平均孔隙半径

第二参数确定单元，用于由压汞曲线对不同孔隙半径下孔隙数目的累积求和，然后同时取毛细管束累计数量n与孔隙半径r的对数，做二者的关系曲线，直线的斜率的绝对值即孔隙分形维数df；利用所述致密油藏岩心的孔隙度φ确定平均迂曲度τav，根据所述致密油藏岩心的孔隙度φ、孔隙分形维数df、最大孔隙半径rmax确定毛细管束模型的特征长度l0；利用所述毛细管束模型的特征长度l0获得毛细管束模型的横截面积a；根据平均迂曲度τav、所述毛细管束模型的特征长度l0、平均孔隙半径确定毛细管束模型的平均迂曲度分形维数dt；

第三参数确定单元，用于确定不同孔隙半径r和不同压力梯度δp下的边界层厚度h；

致密油藏岩心液体渗透率确定单元，用于根据最大孔隙半径rmax、最小孔隙半径rmin、孔隙分形维数df、毛细管束模型的平均迂曲度分形维数dt、边界层厚度h、毛细管束模型的特征长度l0、毛细管束模型的横截面积a确定具有分形特征且考虑液体边界层分布的迂曲毛细管束模型的致密油藏岩心液体渗透率。

优选地，所述模型构建单元构建的具有孔隙分形特征和毛细管束迂曲度分形特征且考虑液体边界层分布的迂曲毛细管束模型的特征为：

所述具有孔隙分形特征和毛细管束迂曲度分形特征且考虑液体边界层分布的迂曲毛细管束模型由一系列不同半径和不同迂曲度的毛细管束组成；其中，孔隙分形特征通过孔隙分形维数df表示；毛细管束迂曲度分形特征通过毛细管束模型的平均迂曲度分形维数dt表示；毛细管束具有分形特征，满足分形关系为：式中：lt(r)为流体路径的实际长度,μm；l0为毛细管束模型的特征长度；dt为毛细管束模型的平均迂曲度分形维数；r为孔隙半径；

每根毛管束考虑了固液吸附形成的不动液体边界层，边界层的厚度h与毛细管束模型中的迂曲毛管束半径，流体粘度μ、驱替压力梯度δp有关，满足表达式：

其中，毛细管束模型中的迂曲毛管束半径与孔隙半径r等价。

优选地，还包括：

液体渗透率随驱替压力梯度变化规律确定单元，用于根据所述具有孔隙分形特征和毛细管束迂曲度分形特征且考虑液体边界层分布的迂曲毛细管束模型致密油藏岩心液体渗透率确定液体渗透率随驱替压力梯度变化规律。

优选地，所述致密油藏岩心液体渗透率确定单元确定的具有分形特征且考虑液体边界层分布的迂曲毛细管束模型的致密油藏岩心液体渗透率的表达式为：

式中，φ表示致密油藏岩心的孔隙度；β1、β2、β3均为流体参数，β1、β2、β3随流体类型的变化而变化；δp为驱替压力梯度，mpa/m；μ为流体粘度，mpa·s。

上述技术方案具有如下有益效果：本技术方案基于分形理论和边界层理论，构建具有分形特征且考虑液体边界层分布的迂曲毛管束模型，利用该模型可以准确表征岩心孔喉结构分布与连通方式，且将边界层厚度公式与具有分形特征的迂曲毛管束模型耦合，提出了一种新的致密油藏液体渗透率计算公式，可以有效的表征液体渗透率随驱替压力的变化规律。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明实施例提出的一种获取致密油藏岩心的液体渗透率的方法流程图；

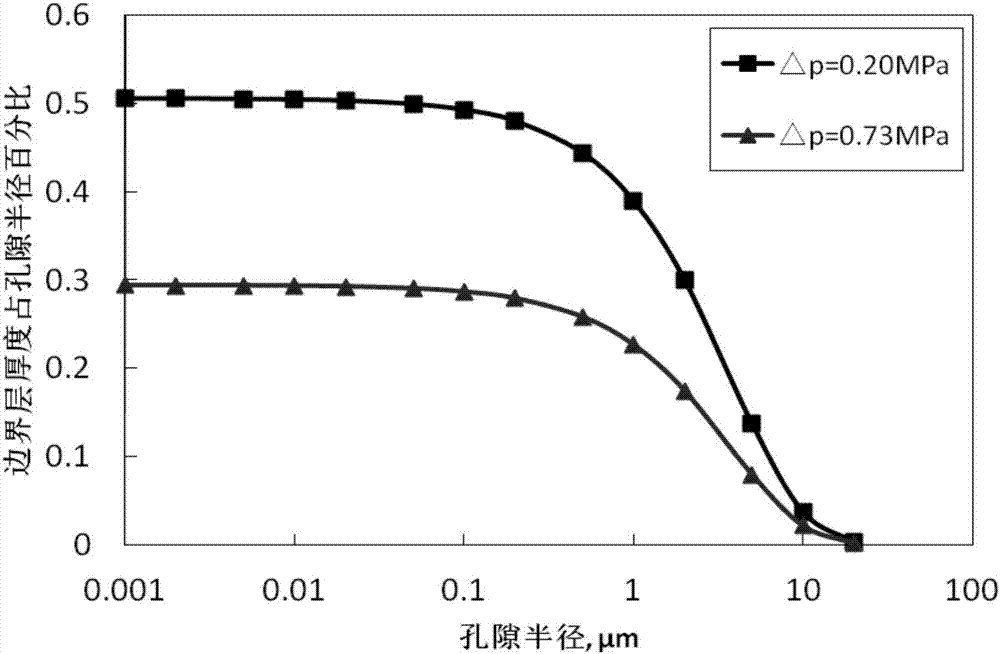
图2为本发明实施例的边界层厚度与孔隙半径的关系曲线图；

图3为本发明实施例的具有分形特征考虑边界层分布的迂曲毛管束模型示意图；

图4为本发明实施例提出的一种获取致密油藏岩心的液体渗透率的装置功能框图；

图5为实施例的岩心压汞曲线图；

图6为本实施例的毛管束累计数量n的对数与孔隙半径r的对数之间的关系曲线图；

图7为本实施例的不同驱替压力梯度下的液体渗透率曲线图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

如图1所示，为本发明实施例提出的一种获取致密油藏岩心的液体渗透率的方法流程图。包括：

步骤101)：构建具有孔隙分形特征和毛细管束迂曲度分形特征且考虑液体边界层分布的迂曲毛细管束模型，获取致密油藏岩心，并得到所述致密油藏岩心的孔隙度φ；

1、孔隙分形特征

根据分形几何理论，若n(＞r)与r服从以下幂率关系

则称多孔介质微观孔隙分布具有分形特征。式中：n(＞r)为岩心中对孔隙半径大于r

的毛管束数量的累积之和；r为孔隙半径,μm；rmax最大孔隙半径，μm；df为孔隙分形维数，无量纲，1＜df＜2。分形物体的数量十分巨大，根据统计理论和方法，认为式(1)是连续且可微的。因此有：

2、具有分形特征的迂曲毛细管束模型

储层岩石内部大量孔隙之间存在相互连通的通道，形成具有各个不同截面的弯曲毛细管束。因此流体在其中经过的是一系列弯曲路径。当流体通过随机且复杂的孔隙结构时，满足如下分形关系：

式中：lt(r)为流体路径的实际长度,μm；l0为毛细管束模型的特征长度，μm；dt为毛细管束模型的平均迂曲度分形维数，无量纲,1＜dt＜3。

3、边界层厚度

实验表明，毛细管半径减小就导致原油边界层厚度增加，边界层作用增强将会引起渗流流体性质的变化。原油在小于1μm的孔道所占比例很大的低渗透油层中流动时，原油边界层的影响显著。边界层厚度表达式如下：

其中，上式系数β1、β2、β3随流体类型的变化而变化，是流体参数，且当μ＝1mpa·s时，数β1＝-0.25763、β2＝-0.261、β3＝-0.419；边界层厚度h与孔隙半径r的单位均为μm；δp为驱替压力梯度，mpa/m；μ为实验流体粘度，mpa·s，另外，在本技术方案中，毛细管束模型中的迂曲毛管束半径与孔隙半径r等价。由图2所示，当孔隙半径小于0.5μm时，边界层厚度占孔隙半径的比例比较大，不可忽略。

4、构建具有分形特征且考虑液体边界层分布的迂曲毛管束模型

所构建的新的模型如图3所示。该模型由一系列不同半径和不同迂曲度的毛细管束组成，毛细管束具有分形分布特征，每根毛管束考虑了固液吸附形成的不动液体边界层，边界层的厚度与毛管束半径，液体粘度、驱替压力梯度有关，并用公式(4)计算。单根毛细管的流量可以有以下公式推导得到。以与管同轴，半径为r的圆柱形流体为研究对象，其在水平方向上所受压力差为：

δf＝δpπr²(5)

式中，δp为驱替压差。

周围流体作用在该圆柱形流体元表面的黏性力为：

流速v随半径r增大而减小，所以速度梯度管内流体做稳定流动，所以以上两力合力为零，即式(5)+式(6)＝0；

分离变量：

对dv积分：

式中，c表示积分常数。

根据边界层临界处液体流速v＝0的条件，求得：

带入上式(8)得毛细管液体流速为：

式中，l0毛细管束模型的特征长度，μm；dt为毛细管束模型的平均迂曲度分形维数。

现在计算圆管内某截面上的流量。将垂直于圆管轴线的圆形截面分成许多细圆环，根据上式以及流量公式可写出通过半径为r，宽度为dr的细圆环的流量：

对上式(13)积分得单根毛管的流量：

对于通过同一横截面迂曲毛细管的总渗流量q可以通过对最小到最大毛细管积分得到：

q(r)表示半径为r时毛细管的流量。

将公式(2)和公式(12)代入公式(13)可以得到毛细管束的总流量：

由达西定律可知，渗透率的表达式为：

将公式(14)代入公式(15)，可以得到所建的新模型的液体渗透率计算表达式为：

步骤102)：对所述致密油藏岩心进行压汞测试，获得岩心压汞曲线；

步骤103)：根据所述岩心压汞曲线确定最大孔隙半径rmax、最小孔隙半径rmin、平均孔隙半径

步骤104)：由压汞曲线对不同孔隙半径下孔隙数目的累积求和，然后同时取毛细管束累计数量n与孔隙半径r的对数，做二者的关系曲线，直线的斜率的绝对值即孔隙分形维数df；利用所述致密油藏岩心的孔隙度φ确定平均迂曲度τav，根据所述致密油藏岩心的孔隙度φ、孔隙分形维数df、最大孔隙半径rmax确定毛细管束模型的特征长度l0；利用所述毛细管束模型的特征长度l0获得毛细管束模型的横截面积a；根据平均迂曲度τav、所述毛细管束模型的特征长度l0、平均孔隙半径确定毛细管束模型的平均迂曲度分形维数dt；

在本步骤中，孔隙分形维数df由公式(1)获得。具体计算过程如下：孔隙个数通过以下公式计算得到：

其中，δvhg(r)是不同孔隙半径变化时对应的压汞增量，由压汞曲线对不同孔隙半径下孔隙数目的累积求和，并同时取毛细管束累计数量n的对数与孔隙半径r的对数，得到lgn(＞r)∝-df·lgr，做二者的关系曲线，直线的斜率的绝对值即分形维数df；毛细管束模型的平均迂曲度分形维数dt计算公式为：

其中，式(18)里平均孔隙半径计算公式为：

式中，si为某一时间点i的汞饱和度、si-1为前一时间点i-1的汞饱和度、ri-1为前一时间点i-1的孔喉半径、ri为某一时间点i的孔喉半径，i表示某一时间点。

平均迂曲度τav计算公式为：

特征长度l0计算公式为：

横截面面积a，单位μm²，计算公式为：

步骤105)：确定不同孔隙半径r和不同压力梯度δp下的边界层厚度h；其中，所述不同孔隙半径r和不同驱替压力梯度δp下的边界层厚度h的表达式为：

其中，β1、β2、β3均为流体参数，β1、β2、β3随流体类型的变化而变化；δp为驱替压力梯度，mpa/m；μ为流体粘度，mpa·s。

步骤106)：根据最大孔隙半径rmax、最小孔隙半径rmin、孔隙分形维数df、毛细管束模型的平均迂曲度分形维数dt、边界层厚度h、毛细管束模型的特征长度l0、毛细管束模型的横截面积a确定具有分形特征且考虑液体边界层分布的迂曲毛细管束模型的致密油藏岩心液体渗透率。

式(16)为具有分形特征且考虑液体边界层分布的迂曲毛细管束模型的致密油藏岩心液体渗透率的计算公式。通过改变不同驱替压力梯度，可以得到不同驱替压力梯度下致密油藏岩心液体渗透率的变化规律。

本领域普通技术人员可以理解实现上述实施例方法中的全部或部分流程，可以通过计算机程序来指令相关的硬件来完成，所述的程序可存储于一般计算机可读取存储介质中，该程序在执行时，可包括如上述各方法的实施例的流程。其中，所述的存储介质可为磁碟、光盘、只读存储记忆体(read-onlymemory，rom)或随机存储记忆体(randomaccessmemory，ram)等。

如图4所示，为本发明实施例提出的一种获取致密油藏岩心的液体渗透率的装置功能框图。包括：

模型构建单元401，用于具有孔隙分形特征和毛细管束迂曲度分形特征且考虑液体边界层分布的迂曲毛细管束模型，获取致密油藏岩心，并得到所述致密油藏岩心的孔隙度φ；

岩心压汞曲线获取单元402，用于对所述致密油藏岩心进行压汞测试，获得岩心压汞曲线；

第一参数确定单元403，用于根据所述岩心压汞曲线确定最大孔隙半径rmax、最小孔隙半径rmin、平均孔隙半径

第二参数确定单元404，用于由压汞曲线对不同孔隙半径下孔隙数目的累积求和，然后同时取毛细管束累计数量n与孔隙半径r的对数，做二者的关系曲线，直线的斜率的绝对值即孔隙分形维数df；利用所述致密油藏岩心的孔隙度φ确定平均迂曲度τav，根据所述致密油藏岩心的孔隙度φ、孔隙分形维数df、最大孔隙半径rmax确定毛细管束模型的特征长度l0；利用所述毛细管束模型的特征长度l0获得毛细管束模型的横截面积a；根据平均迂曲度τav、所述毛细管束模型的特征长度l0、平均孔隙半径确定毛细管束模型的平均迂曲度分形维数dt；

第三参数确定单元405，用于确定不同孔隙半径r和不同压力梯度δp下的边界层厚度h；

致密油藏岩心液体渗透率确定单元406，用于根据最大孔隙半径rmax、最小孔隙半径rmin、孔隙分形维数df、毛细管束模型的平均迂曲度分形维数dt、边界层厚度h、毛细管束模型的特征长度l0、毛细管束模型的横截面积a确定具有分形特征且考虑液体边界层分布的迂曲毛细管束模型的致密油藏岩心液体渗透率。

优选地，所述模型构建单元构建的具有孔隙分形特征和毛细管束迂曲度分形特征且考虑液体边界层分布的迂曲毛细管束模型的特征为：

所述具有孔隙分形特征和毛细管束迂曲度分形特征且考虑液体边界层分布的迂曲毛细管束模型由一系列不同半径和不同迂曲度的毛细管束组成；其中，孔隙分形特征通过孔隙分形维数df表示；毛细管束迂曲度分形特征通过毛细管束模型的平均迂曲度分形维数dt表示；毛细管束具有分形特征，满足分形关系为：式中：lt(r)为流体路径的实际长度,μm；l0为毛细管束模型的特征长度；dt为毛细管束模型的平均迂曲度分形维数；r为孔隙半径；

每根毛管束考虑了固液吸附形成的不动液体边界层，边界层的厚度h与毛细管束模型中的迂曲毛管束半径，流体粘度μ、驱替压力梯度δp有关，满足表达式：

其中，毛细管束模型中的迂曲毛管束半径与孔隙半径r等价。

优选地，还包括：

液体渗透率随驱替压力梯度变化规律确定单元，用于根据所述具有孔隙分形特征和毛细管束迂曲度分形特征且考虑液体边界层分布的迂曲毛细管束模型致密油藏岩心液体渗透率确定液体渗透率随驱替压力梯度变化规律。

优选地，所述致密油藏岩心液体渗透率确定单元确定的具有分形特征且考虑液体边界层分布的迂曲毛细管束模型的致密油藏岩心液体渗透率的表达式为：

式中，φ表示致密油藏岩心的孔隙度；β1、β2、β3均为流体参数，β1、β2、β3随流体类型的变化而变化；δp为驱替压力梯度，mpa/m；μ为流体粘度，mpa·s。

本领域技术人员还可以了解到本发明实施例列出的各种功能是通过硬件还是软件来实现取决于特定的应用和整个系统的设计要求。本领域技术人员可以对于每种特定的应用，可以使用各种方法实现所述的功能，但这种实现不应被理解为超出本发明实施例保护的范围。

此外，尽管在上文详细描述中提及了装置的若干单元，但是这种划分仅仅并非强制性的。实际上，根据本发明的实施方式，上文描述的两个或更多单元的特征和功能可以在一个单元中具体化。同样，上文描述的一个单元的特征和功能也可以进一步划分为由多个单元来具体化。

实施例

1.取一块致密油藏岩心，通过饱和水称重法测得岩心孔隙度φ＝0.1541；

2.对岩心进行压汞测试，获得岩心压汞曲线，如图5所示。根据图5可知，最大孔隙半径：

岩心最小孔隙半径rmin：

该式中，r”min表示根据压汞数据计算出来的最小孔隙半径；

对于不同的驱替压力梯度可以根据求出含边界层的最小孔隙流动半径的大小；其中，r'min表示由边界层变换公式计算出来的可流动的最小半径，所以rmin取r'min，r”min中最大值。

3.先对不同半径对应的毛细管束进行累积得：

取毛细管束累计数量n与孔隙半径r的对数，作在双对数坐标图上求斜率：

lgn(＞r)∝-df·lgr

根据上式得毛细管束累计数量n的对数与孔隙半径r的对数之间的关系曲线图，如图6所示。曲线斜率的绝对值即分形维数，该岩心的分形维数为：df＝1.9704。

该岩心的平均孔隙半径为：

计算平均迂曲度τav为：

毛细管束模型的特征长度为：

毛细管束模型的横截面积为：

将以上得的参数带入公式(19)，毛细管束模型的平均迂曲度分形维数为：

将上述参数汇总一起，得到致密油藏岩心的参数，请见下表1。

表1

4.取驱替压力梯度δp范围改为0.1～0.9mpa/m，取致密岩心中流体粘度μ＝1mpa·s，代入下式计算不同驱替压力梯度下的液体渗透率：

根据上式可获得不同驱替压力梯度下的液体渗透率的曲线图，如图7所示。现有的技术比如室内实验法，是通过室内流体驱替实验，并结合达西定律测量岩心液体渗透率。这种方法取芯成本高，能获取的天然岩心数量少，实验费用巨大；由于致密岩心渗透率极低，驱替实验达到驱替平衡时间长，且实验得到的液体渗透率误差较大；致密油藏岩心具有明显的非达西渗流特征，随着驱替压力梯度的变化，液体边界层的厚度发生变化，继而液体渗透率发生变化。因此，不同驱替压力下得到的液体渗透率不同，目前的实验通常只测定单一压力梯度下的液体渗透率，由于实验时间长，且测量精度不高，不同驱替压力下液体渗透率实验很少开展，因此不能准确描述致密油藏岩心液体渗透率随驱替压力变化而发生变化的规律。

以上所述的具体实施方式，对本发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本发明的具体实施方式而已，并不用于限定本发明的保护范围，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。