基于改进的SmartDFT算法的非平衡系统频率估计方法与流程

本发明涉及非平衡系统频率估计技术领域，特别是涉及基于改进的smartdft算法的非平衡系统频率估计方法。

背景技术：

在附加白高斯噪声下，估计正弦信号或复指数信号的频率、幅度、相位是非常重要的非线性问题，在电力系统分析、无线通信、雷达信号监测和语音分析中有着广泛的应用。在不同的应用中，众多文献也提出了相对应的估计方法，如基于dft算法，最小二乘算法，自适应陷波器，卡尔曼滤波器和它的拓展，最大后验概率算法和基于子空间投影的算法。

典型的，标准的n点dft操作在频谱上可以得到2π/n的分辨率，但是在异步采样下是不准确的。传统方法上如果想要提高基于dft的频率估计算法的精确度，额外的计算复杂度不可避免。在已有文献中，提出过了一种smartdft(sdft)技术改善实时正弦信号频率估计的准确度。也有文献进一步应用了复值最小二乘框架改善了sdft的估计效果。基于窗口dft的插值算法可以获得频率估计的重要改善，因为信号序列的窗口可以减少频谱泄漏和频谱插值。dft算法的相角误差可以估计相应模拟信号的真实频率,由非相干dft采样引起的泄漏效果也可以用于频率估计。进一步，有文献提出采用两个阶段去改善估计效果，第一阶段实行n点dft的粗估计，接着在频谱峰值附近进行第二阶段的精确估计。

非圆信号广泛应用于描述非平衡系统的动态状态，例如非平衡三相电力系统、i-q不平衡通信系统等等。基于恰当的非圆信号统计分析，利用非平衡电压的非圆统计特性，众多文献提出了一系列的估计模型，标准的频率估计算法也可以进一步扩展为通用的形式。

无论是频域的sdft技术还是时域的rphd技术还无法处理非平衡系统中的复值非圆信号，本专利意义在于基于复值非圆信号的特性，实现与以上技术的结合，完成在有噪条件下，对复值非圆信号频率精确的估计和追踪。

技术实现要素：

为了解决上述存在的问题，本发明提供基于改进的smartdft算法的非平衡系统频率估计方法，扩展了原始的smartdft技术(sdft)，使此项技术不仅可以应用于实值正弦信号，也可以处理复值非圆信号。基于连续dft基频分量间的线性预测(lp)性质，应用最小二乘框架可以减小模型的均方误差，得到改进的复值最小二乘算法(cls)。同时，专利还提出了一种复值改进的pisarenko谐波分解算法(crphd),此方法可以移除噪声的干扰获得精确的频率估计，可以有效应用在含有噪声的非平衡三相电力系统中，为达此目的，本发明提供基于改进的smartdft算法的非平衡系统频率估计方法，具体估计方法如下：

步骤1计算非圆信号第k点频率分量：

没有噪声和谐波干扰的非平衡系统中的非圆信号可以表示为：参数α和β分别定义为这里a,b和是未知的确定性常量分别表示当前信号的幅度和相位，定义信号频率这里k∈{1,2,…,n-1}，δ∈(0,1)分别是未知系统频率的整数和小数部分，目标是根据n点dft变换后的第k频点序列{xk(m)}找到ω0；

信号x(n)第k点dft频率分量如下：

步骤2无噪条件下的sdft算法：

现在提出频率估计算法：用定义参数的估计值；

定义公式(1)中的指数内核为；

如此，根据公式(1)和(2)，找到如下的关系：ak(m+1)＝rak(m)和bk(m+1)＝r^-1bk(m)，以及：

对公式(3)进行代数变换后，可以找到连续dft分量的线性预测关系：xk(m+1)+xk(m-1)＝μxk(m)，这里可以通过下式估计

因此，sdft算法可以通过计算来估计系统频率这里表示取复数的实部；

步骤3有噪条件下cls优化处理：

现在考虑在噪声环境下的非平衡系统：噪声q(n)是均值为零，方差为的高斯白过程，继续使用复值最小二乘cls框架改善了智能离散傅里叶变换sdft算法的性能，同样，将此方法应用于非平衡系统信号上，基于cls的算法利用了序列的线性预测性质：然后最小化误差e(n)的平方和：这里qk(m)是噪声q(n)的dft变换；

组合l点序列定义向量相应的误差向量为此误差向量的共轭转置形式可表示为cls框架作用在于找到一个最优的值以最小化均方误差：令则提出的cls改进sdft的算法可以表示如下：

步骤4有噪条件下crphd实现进一步抗噪优化：

另一方面，重新考虑均方误差值继续推导如下：

这里是q(m)的方差，由于公式(6)的第二项是关于的噪声项，一般情况下并不在取得最小值，这也是cls算法估计含噪信号的劣势所在，在非平衡系统中使用复值rphd方法crphd，如公式(6)所示，为了移除噪声对频率估计误差的影响，依据来最小化重新定义一个新的代价函数为：

步骤5寻求最优的值最小化计算求解频率估计值：

为了找到最优的值最小化求偏导令其等于零：

这里：

尽管公式(8)的最后推导式有两个根，但只有一个根可以表示频率估计量，如此推导得到

了相对于cls更加抗噪的，适用于复值非圆信号的crphd频率估计方法，如下所示：

本发明的进一步改进，步骤二，通过下面的方法根据xk(m+1),xk(m)和xk(m-1)的值可以估计k和δ；

1)基于dft最大点的位置进行频率粗估计：

2)估计δ：定义公式(1)前一项为a(m)，第二项为b(m)，这样公式(1)中的xk(m)表示为：xk(m)＝ak(m)+bk(m)。

本发明基于改进的smartdft算法的非平衡系统频率估计方法，本申请扩展了原始的smartdft技术(sdft)，使此项技术不仅可以应用于实值正弦信号，也可以处理复值非圆信号。基于连续dft基频分量间的线性预测(lp)性质，应用最小二乘框架可以减小模型的均方误差。同时，提出了一种复值改进的pisarenko谐波分解算法(crphd)，此方法可以移除噪声的干扰获得精确的频率估计。本发明在含有噪声的非平衡三相电力系统中，经过仿真显示本申请所提出算法的优越的抗噪性能。

附图说明

图1为不同信噪比下频率估计算法的均方误差对比图；

图2为两种算法在频率波动下的频率跟踪性能图(a)系统频率经历频率调制(b)系统频率经历了上升和下降；

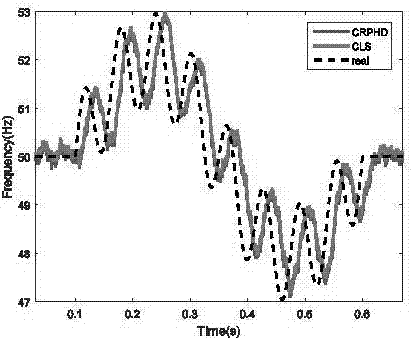
图3真实环境非平衡三相电力系统中的频率估计效果图(a)三相电压幅值波动(b)频率估计效果。

具体实施方式

下面结合附图与具体实施方式对本发明作进一步详细描述：

本发明提供基于改进的smartdft算法的非平衡系统频率估计方法，扩展了原始的smartdft技术(sdft)，使此项技术不仅可以应用于实值正弦信号，也可以处理复值非圆信号。基于连续dft基频分量间的线性预测(lp)性质，应用最小二乘框架可以减小模型的均方误差，得到改进的复值最小二乘算法(cls)。同时，专利还提出了一种复值改进的pisarenko谐波分解算法(crphd),此方法可以移除噪声的干扰获得精确的频率估计，可以有效应用在含有噪声的非平衡三相电力系统中。

具体实施例1如下：

在这部分，我们将利用matlab平台展示专利算法的仿真结果。我们分别设置采样频率为fs＝1600，基点频率为f0＝50，这样，为了计算dft的基础频率，系统电压的采样点需要设置为n＝fs/f0＝32。同时，我们将估计算法的窗长设置为l＝15。

首先，我们评估在噪声环境下crphd算法相对于cls优越的估计性能。非平衡系统电压真实频率f＝f0+δf设置在51hz，将不同信噪比条件下的噪声加入系统中，图1展示了crphd和cls频率估计算法的均方误差，如图所示，所提出的crphd算法在性能上与cls相似，但在低信噪比条件下，它的估计效果将优于cls算法。

具体实施例2如下：

本组仿真，我们将研究在频率波动情况下，不同估计算法的频率跟踪性能。在原始非平衡系统基础上，信号在0.1s到0.6s经历了复合的正弦频率调制f(t)＝50+2sin(4π(t-0.1))+sin(32π(t-0.1))，这里ω0(t)＝2π·f(t)，同时系统加入10db噪声。如图2(a)所示，两种算法都可以快速而又准确的跟踪到系统频率的动态变化。图2(b)中，非平衡系统在t＝0s时加入40db的噪声，同时系统频率经历了1hz/s的上升，然后在50.1hz处保持了0.2s，紧接着从0.5s到0.6s经历了1hz/s的下降。在所有情况下，两种算法都精准跟踪到了频率变化。

具体实施例3如下：

最后一组仿真，我们在真实世界电力系统下研究所提出算法的鲁棒性。三相电压信号记录在110/20/10kv的变电站中。所要测量的三相电压系统频率大约在50hz附近，经过了1khz的采样，电压幅值根据峰值进行了归一化处理。在图3(a)中，所示电压在0.27s至0.54s左右经历了非平衡状态，如图3(b)所示，虽然出现了短暂的波动，两种算法在平衡和非平衡电压情况下都获得了准确的频率估计效果。

以上所述，仅是本发明的较佳实施例而已，并非是对本发明作任何其他形式的限制，而依据本发明的技术实质所作的任何修改或等同变化，仍属于本发明所要求保护的范围。