一种基于稀疏阵的近场相干源的无源定位方法与流程

本发明属于无源定位技术领域，特别涉及基于稀疏阵的近场相干源的无源定位技术。

背景技术：

无源定位是指自身不辐射电磁波的定位系统仅通过被动地接收目标辐射或反射的电磁信号，利用各个站点接收信号的时间、相位等信息差异，快速准确地获取目标距离与方位信息，在电子侦察、电子干扰等中具有重要的应用价值。无源定位可分为远场无源定位与近场无源定位:若目标辐射的电磁波到达各测量站点可近似为平面波，则称该类目标的定位为远场无源定位；若目标辐射的电磁波到达各测量站点可近似为球面波，则称为近场无源定位。

在军事电子体系的对抗中，复杂电磁环境下的雷达生存和探测能力将受到极大的挑战。实际信号环境中，多径效应和复杂电磁干扰会产生大量的强相关和相干信号，导致协方差矩阵秩亏，使得子空间类doa估计算法失效。文献“sourcelocalizationandsensing:anonparametericiterativeadaptiveapproachbasedonweightedleastsquares.ieeetransactionsonaerospaceandelectronicsystems,vol.46,no.1,pp.425-443,jan.2010.”中针对远场的相干源信号，提出了基于自适应迭代的算法；该算法通过迭代解相干实时自适应调整满足最小方差无失真准则的空域滤波器系数，从而可估计相干源信号、有限快拍等信号的角度，可应用于稀疏非均匀阵列，增大阵列孔径和方位角分辨力。然而，当信号源位于近场时，自适应迭代算法需要构造非常大维度的导向矩阵，因此具有非常大的计算复杂度，从而无法实时有效探测信源位置。因此，研究一种搜索维度小、分辨力高、计算复杂度小，工程实用性强的近场无源定位方法在实际中具有重要的应用价值。

技术实现要素：

本发明所要解决的技术问题是，提供一种搜索维度小、天线阵列少、分辨力高、计算复杂度小、工程实用性强的近场相干源定位方法。

本发明采用的技术方案是，本发明使用一种基于稀疏阵的近场相干源的无源定位方法，包括以下步骤；

步骤1：将整个线性阵列分为三个子阵；设整个线阵孔径为d，阵元总个数为m；子阵1位于线阵的左侧，孔径为d1，阵元个数为m1；子阵2位于线阵的右侧，孔径为d2，阵元个数为m2，di＜＜d，i＝1,2；使得目标相对于子阵1和子阵2为远场信号，相对于整个阵列为近场信号；

步骤2：子阵1和子阵2使用自适应迭代算法估计远场方位角；

子阵1和子阵2的输入信号分别为y1(n)和y2(n)，y3(n)为整个阵列输入信号；目标信号记为s(n)，通过空域滤波器近似恢复出目标信号记为根据恢复出的目标信号，计算出各目标对于子阵1和子阵2的的方位角；设共有p个目标，子阵1和子阵2分别使用自适应迭代算法对目标进行方位角估计，测得第p个目标对于子阵1和子阵2的方位角分别为θ1p，θ2p；

步骤3：根据各目标对于子阵1和子阵2的方位角，由正弦定理可求得第p个目标到子阵1和子阵2的距离r1、r2；

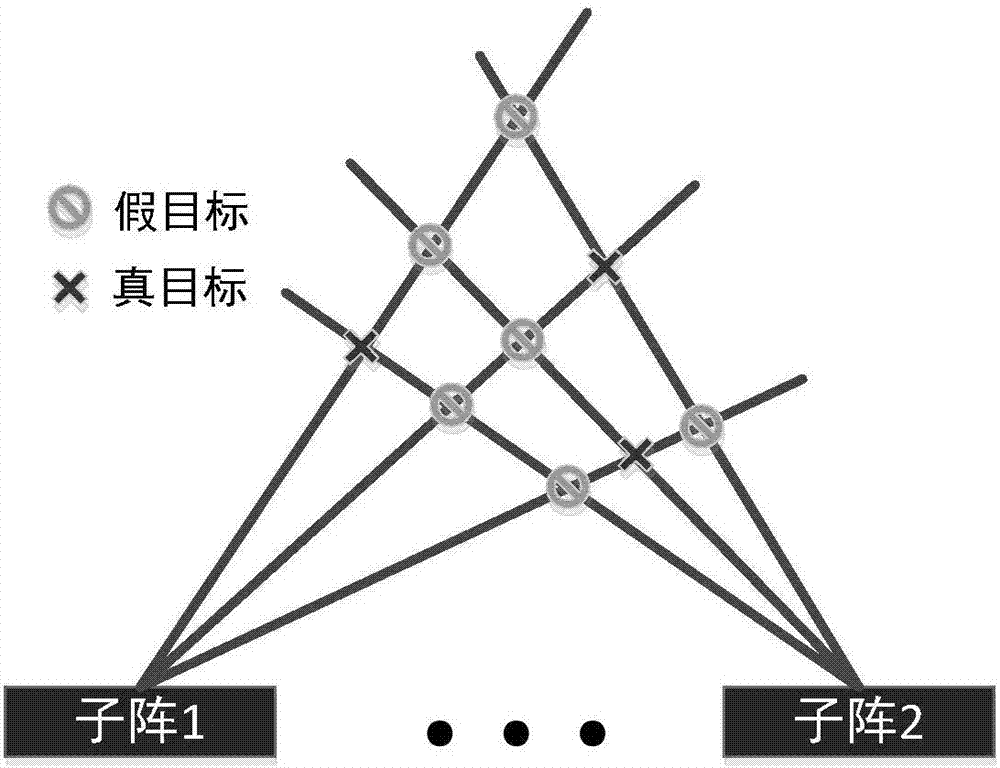
设子阵1测得p1个目标，子阵2测得p2个目标，则形成至多p1p2个交点，这些交点为目标位置候选点；

步骤4：通过整个阵列接收的信号定位近场目标，在步骤3计算出的目标位置候选点周围使用自适应迭代算法进行小范围搜索，直到角度和距离搜索精度达到要求为止。

进一步的，所述步骤2中方位角的计算方法为：

步骤2.1：首次迭代前，采用常规波束形成方法的空域滤波器恢复估计目标信号的功率记为

步骤2.2：第q次迭代时，由归一化构成的对角矩阵p^(q-1)估计输入信号y1(n)的自相关矩阵将估计所得的自相关矩阵带入最小方差无失真准则的空域滤波器恢复估计目标信号的归一化功率p^(q)；

步骤2.3：计算相邻两次迭代得到的归一化功率差的2范数，对是否停止迭代进行判定：如果其值小于设定的收敛值，则停止迭代，输出最后一次迭代得到的信号功率向量；如果其值大于设定的收敛值，重复步骤2.2-2.3，直到满足条件为止；

步骤2.4：对功率幅度进行谱峰搜索得到真实目标所在方位角估计值。

本发明提供了一种基于稀疏阵的近场相干源的无源定位方法。该方法通过构造对角矩阵估计接收信号自相关矩阵解相干，适用于相干源、相关源、非相干源，对阵列的几何构型几乎没有要求，因此能够以较低成本实现大孔径和较高分辨力。通过远近场结合的思想，可以缩小近场目标的搜索范围，快速实时的定位近场目标位置，工程实用性强。

附图说明

图1为本发明的近场窄带接收信号几何结构图；

图2为阵列结构及子阵测角交点图；

图3为步骤2中自适应迭代算法的流程图；

图4为子阵方位角估计图；

图5(a)、(b)分别为两个相干源在步骤4.3后的局部二维谱峰图；

图6(a)、(b)分别为两个相干源确定方位角后在距离像上进行搜索的切面图。

具体实施方式

步骤1：如图1所示，设近场无源定位的天线阵列系为线阵列且布阵范围为[0,d]，阵元个数为m。其中，d表示阵列孔径，单位为米。随机稀疏布阵的位置可以以如下方式描述：在位置0以及位置d处各布置1个阵元且位置分别设为d1与dm，在(0,d)米范围内以随机均匀分布的方式放置m-2个阵元，其位置分别为d2,…,dm-1。将整个线性阵列分为三个子阵，设子阵1位于线阵的左侧，孔径为d1，阵元个数为m1。子阵2位于线阵的右侧，孔径为d2，阵元个数为m2。使得目标相对于子阵1和子阵2为远场信号，相对于整个阵列为近场信号。即该阵列探测目标距离r范围为

其中，λ为接收信号波长，max(·)表示最大值。

步骤2：子阵1和子阵2使用自适应迭代算法估计远场方位角。

子阵1和子阵2的接收信号分别为y1(n)和y2(n)，y3(n)为整个阵列接收信号。原目标信号记为s(n)，通过空域滤波器近似恢复出目标信号记为目标对于整个阵列为近场目标。假设为搜索角度，θ1,θ2,…,θk表示搜索角度值，k表示搜索角度个数，共有p个信源，第p个信源距子阵1的距离为r1p，方向θp，定义其坐标为(r1p,θp)，设第p个信源到达第m个阵元的距离为第m个阵元接收信源p相对于参考阵元的相对延迟为δrmp＝rmp-r1p。

整个阵列接收的回波信号用矢量表示为

y3(r,θ,n)＝a(r,θ)s(n)+v(n)

其中，y3(r,θ,n)＝[y3,1(r,θ,n)y3,2(r,θ,n)…y3,m(r,θ,n)]^t，n表示快拍，[·]^t表示向量或矩阵的转置，s(n)＝[s1(n)s2(n)…sp(n)]^t，p为信源个数，v(n)＝[v1(n)v2(n)…vm(n)]^t表示高斯零均值随机白噪声，a(r,θ)＝[a(r1,θ1)a(r2,θ2)…a(rp,θp)]，δrmp表示第m个阵元接收信源p相对于参考阵元的延迟；

由阵列几何关系可知，y1(n)为y3(n)的前m1行，y2(n)为y3(n)的后m2行。信源对子阵1和子阵2为远场信号,因此y1(n)与y2(n)可用远场信号形式表示。在窄带信号中，子阵1和子阵2第n个快拍的接收信号可以表达为

yo(n)＝ao(θ)s(n)+vo(n),n＝1,…,n,o＝1,2

其中，n为快拍总数，vo(n)，o＝1,2为子阵o接收的零均值高斯白噪声。由于信源对子阵1和子阵2为远场信号，导向矩阵ao(θ)，o＝1,2与距离无关，则ao(θ)＝[ao(θ1),ao(θ2),…,ao(θk)]，其中f为中心频率，θk表示第k个搜索角度，c0为电磁波传播速度，e(·)表示指数函数，j表示虚数单位，子阵2测角方法与子阵1相似，以子阵1为例，估计远场方位角的步骤如下：

步骤2.1：首次迭代前，采用常规波束形成方法的空域滤波器恢复

其中，是的第k个元素，(·)^h表示矩阵或向量的共轭转置。

步骤2.2：则由估计的目标信号可得对应的功率其第k个元素可表示为

其中，|·|表示求模运算，∑为求和符号，为k×1的向量；

步骤2.3：将中的元素归一化得将作为k×k维对角矩阵p⁽⁰⁾的对角元素，更别表示每个目标对应的功率；

步骤2.4：当第q次迭代(q≥1)时，由p^(q-1)估计输入回波信号的自相关矩阵

其中，σ²为噪声的方差，i为对角矩阵，其对角元素均为1。

步骤2.5：根据最小方差无失真准则设计空域滤波器，输出为目标信号的估计值

其中，k＝1,2,…k，(·)^-1表示矩阵求逆。

步骤2.6：估计的目标信号的功率为的第k个元素为

步骤2.7：将中的元素归一化得将作为k×k维对角矩阵p^(q)的对角元素。

步骤2.8：计算相邻两次迭代得到的归一化功率差的矩阵2范数，对是否停止迭代进行判定：如果||p^(q)-p^(q-1)||＜ε(ε为设定的收敛值)，则停止迭代，输出最后一次迭代得到的功率如果其值大于设定的收敛值，则更新递增迭代次数，重复步骤2.4-2.7，直到满足条件为止。

步骤2.9：对目标功率进行谱峰搜索，寻找其p个极大值，得到真实目标所在方位角估计值。

步骤3：设共有p个目标，子阵1和子阵2分别使用自适应迭代算法对目标进行方位角估计，测得第p个目标角度分别为θ1p，θ2p。则由正弦定理可求得第p个目标到子阵1和子阵2的距离r1、r2。

设子阵1测得p1个目标，子阵2测得p2个目标，则形成至多p1p2个交点，这些交点包含了目标的真实位置。

步骤4：通过整个阵列接收的信号定位近场目标，在估算出的目标位置周围使用自适应迭代算法进行小范围搜索，直到角度和距离搜索精度达到要求为止。

步骤4.1：由步骤3得到若干个交点，分别记为(li,αi),i＝1,2,…w。其中，w为交点总个数，αi为子阵1估计的方位角，li为由步骤3对应αi计算得到的信源与子阵1的距离，在交点(li,αi),附近搜索

步骤4.2：假设搜索角度范围为q表示搜索的角度个数，搜索距离范围为[gi,1,gi,2,…gi,t]，li＝(gi,1+gi,q)/2，t表示搜索的距离个数；将搜索二维区域排成一维，即则针对搜索的第k个格点对应坐标为由步骤2中近场模型可求得表示第k个格点对应的导向矢量，将简记为bk。

步骤4.3：将bk带入到步骤2中的a1(θk)，同时y3(n)取代y1(n)，a(r,θ)取代a1(θ)，重复步骤2.1-2.5。对目标功率进行谱峰搜索，寻找其p个极大值对应的格点分别为u1,…,up，根据格点和坐标的对应关系，得到目标所在位置分别为

步骤4.4：在附近重复步骤4.2-4.3进行搜索，直到搜索达到角度和距离精度要求。

本发明的效果通过以下仿真实验进行说明：

在孔径为100m的阵列上随机布阵30个阵元，其中分别有12个阵元随机分布在孔径为10m的子阵1和子阵2上。回波信号频率为1ghz，两个相干源目标分别位于(3000m,-15°)、(8000m,20°)，噪声为零均值高斯白噪声，方差为1，信噪比为20db。

如图4所示，由步骤2子阵1测得两个相干源方位角分别为-15.1°、20°；子阵2测得方位角为-16.7°、19.4°。通过步骤3计算得到3个交点的坐标为(3430.4m,-15.1°)、(160.3m,-15.1°)和(9007.3m,20°)。由步骤4近场搜索最后得到目标位置为(3000.4m,-15°)和(8001.3m,20°)。仿真结果表明，本发明提出的方法能够有效的估计相干源位置，同时利用远近场的结合的思想，能够大大减少计算量，工程实用性强。