一种面向多重应用的被动式定位方法与流程

本发明涉及无线定位技术领域，具体涉及一种面向多重应用的被动式定位方法，该方法无需大规模训练学习，并且在廉价商用设备与专用设备上兼有效，普适性强，具有良好的鲁棒性和定位效果。

背景技术：

无线定位技术发展到今天，已经成为沟通人与科技的桥梁，并且成为过去二十年的重要研究方向。无线定位技术的研究和普及，为智能家居、雷达定位、卫星导航、安全防盗、行为监测、商品识别等带来了无限可能，同时带来了巨大的应用需求和市场前景，并成为我们生活的重要组成部分。当今无线定位技术不但成为无线通信、传感网和物联网的研究热点(如sigcomm、mobicom、mobisys、nsdi、ipsn等旗舰会议都有无线定位方向稳定的主题)，更成为texasinstruments、linear等高科技公司技术创新和应用热点。

当前无线定位技术最具代表性工作有mit的d.katabi，指尖戴上rfid标签在空中滑动就可以实现英文单词输入，实现了人类虚拟输入屏幕的梦想。然而现有定位方法要求目标携带设备主动参与到定位过程中，即主动式定位技术，难以适用目标无法或不方便携带设备的行为监测场景。

相反，被动式定位技术则不需目标携带设备，同时具备数据处理方便并且对视线和监测视角要求不高等优点，因此是当今行为监测的有效解决方案之一。从国际前沿进展可以看到，以感知信号扰动为中心的被动式定位，将在未来极大的改变和影响人类生活而成为历史上最为精彩的一刻，刘云浩等在商场实现无需顾客参与的消费者移动轨迹跟踪，实现了“无意识协作感知”，突破了“专门人员参与”这个壁垒。同时，被动式定位也促进了新型无需视频头参与的人机交互方式出现，d.katabi利用调频连续波分辨目标手臂指向；q.pu等提取不同手势引起的多普勒频偏，实现9种手势识别。但是现有的被动式定位方法为达到高精度，要么需要大规模训练学习从而导致勘测代价大，要么需要专用设备导致应用场景受限。

技术实现要素：

针对上述现有技术中存在的问题，本发明的目的在于，提供一种无需学习、通用性好的被动式目标定位方法，以克服现有被动式定位技术勘测代价大、应用场景受限的弊端。

为了实现上述任务，本发明采用以下技术方案：

一种面向多重应用的被动式定位方法，包括以下步骤：

步骤一，在监测区域内部署一个无线信号发送设备，两个无线信号接收设备，三个设备不共线；

步骤二，在监测区域内没有目标时，两个接收设备均采集1组发送设备发出的无线信号；当待测目标进入监测区域后，两个接收设备均采集r组无线信号；

步骤三，针对上述每一个接收设备在监测区域内有目标、没有目标时采集的无线信号，对每一个接收设备的阵列天线中每一个阵元采集得到的每一组无线信号均进行相位的提取，对提取的相位信息进行线性变换以获取可用的相位特征信息；

步骤四，对于每一个接收设备在监测区域内有目标、没有目标时采集的无线信号，分别建立每一个接收设备的阵列天线上所有阵元的信号接收矩阵；

步骤五，根据步骤四得到的不同信号接收矩阵，得到待测目标进入监测区域后无线信号到达两个接收设备的到达角度，以实现待测目标的定位。

进一步地，所述的可用的相位特征信息是指：

记两个接收设备分别为接收端一和接收端二，每个接收设备的阵列天线均有多个阵元，记每一个接收设备上其中一个阵元为参考阵元，其余的阵元为接收阵元；

当监测区域中没有目标时，接收端一采集无线信号记为情况一，接收端二采集无线信号记为情况二；待测目标进入监测区域后，接收端一采集无线信号记为情况三，接收端二采集无线信号记为情况四；分别计算在每一种情况下：

接收端一和接收端二的每个接收阵元接收到的信号的相位特征信息减去该接收端的参考阵元接收到的相位特征信息，从而获取每个接收阵元相对于参考阵元引起的相位差。

进一步地，所述的步骤四中，信号接收矩阵的建立过程为：

接收设备的阵列天线在接收无线信号时，无线信号到达接收阵元的时间相对于到达参考阵元的时间存在延迟；令无线信号的传播延迟在第一个接收阵元上引起的相位差为τi，则在第二个接收阵元引起的相位差为2τi，在第m-1个接收阵元引起的相位差为(m-1)τi，记监测区域内有p个信号源，天线阵列共包含m个阵元，则所有信号源发出的信号si(n)到达不同阵元的相位差组成的向量矩阵a(τ)表示为：

上式中：

a(τi)表示第i(i＝1,2...,p)个信号源发出的信号到达m个阵元的相位差所组成的向量；

τi表示信号si(n)电波传播延迟在第一个接收阵元引起的相位差；

j表示虚数单位，m表示阵元数目；

设不同阵元上的加性观测噪声为：e(n)＝[e1(n),...,em(n)]^t，其中ei(n)表示信号到达第i(i＝1,2,...m)个阵元上的加性噪声，则所有阵元的信号接收矩阵表示为：

上式中：

s(n)＝[s1(n),...,sp(n)]^h

其中h表示转置。

进一步地，步骤五的具体过程包括：

步骤5.1，对于所述的信号接收矩阵，计算其对应的协方差矩阵r；对协方差矩阵r进行特征值分解，得到g个特征值和对应的特征向量；在g个特征值中，有g-p个相等的小的特征值以及p个大的特征值；将p个大的特征值对应的特征向量构成信号子空间us；将相等的小的特征值对应的特征向量构成噪声子空间un，这两个子空间正交；利用两个子空间计算谱函数，则谱函数的所有峰值对应的角度即为无线信号达到各个阵元的角度；

步骤5.2，区分监测区域内的静止干扰源和除了待测目标之外的其他移动干扰源，并消除移动干扰源和静止干扰源；

步骤5.3，利用三角测量法确定待测目标的位置。

本发明与现有技术相比具有以下技术特点：

1.本发明通过获取接收端的不同天线接收信号的稳定相位差，结合参考阵列天线的位置来实现基于到达角度的目标定位，保证了商用设备下的定位精度；

2.本发明利用静止干扰源的角度误差补偿来缓减信号到达角度随时间产生的偏移；其次利用不同种类反射信号之间的相干与非相干性，对环境中移动干扰源和静止干扰源反射信号的到达角度进行消除，实现了高鲁棒性和高精度的目标反射信号到达角度估计。

3.本发明不需要大规模的训练学习，从而解决勘测代价问题；

4.本发明在廉价商用设备与专用设备上兼可有效工作，在实际应用中具有很好的普适性。

附图说明

图1为本发明方法的系统流程图；

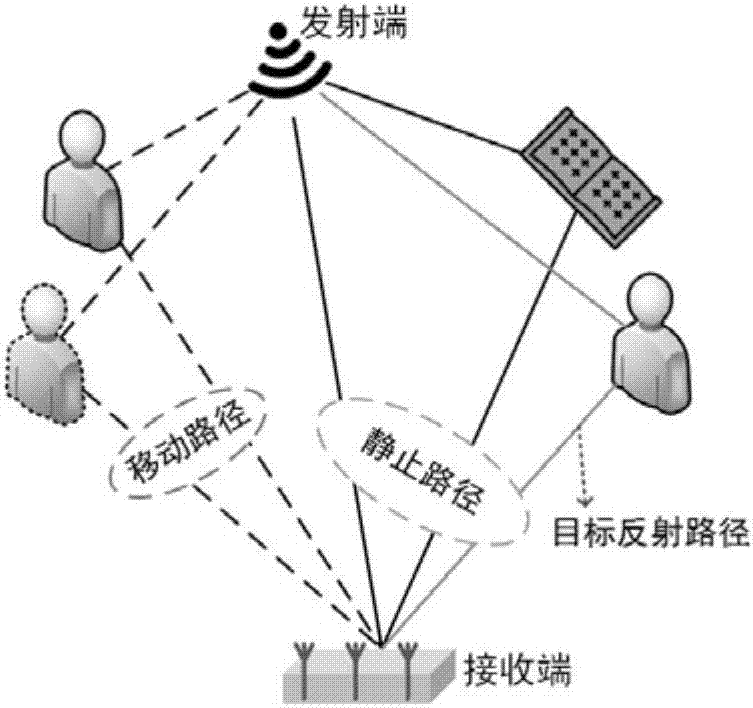
图2为无线信号多径传播的模型图；

图3为接收设备上阵列天线接收信号的示意图；

图4为步骤三中所述的相位提取前后的结果图；

图5为消除移动干扰源和静止干扰源结果图，其中(a)为区分移动信源与静止信源的示意图；(b)为解相干前的示意图；(c)为解相干后的示意图；

图6为真实实验环境与设备布设示意图，其中其中(a)为室内空旷条件下的示意图；(b)为室内环境简单时的示意图；(c)为室内环境复杂时的示意图；

图7为图6的三种实验场景下定位误差分析图；其中(a)为图6中(a)情况的分析图，其中(b)为图6中(b)情况的分析图，其中(c)为图6中(c)情况的分析图；

图8为不同接收设备数目及不同移动干扰目标数目下定位误差分析图；其中(a)(b)为usrp设备的分析图，(c)和(d)为wi-fi设备的分析图；

图9为到达角度的估计误差分析图；其中(a)为usrp设备的分析图，(b)为wi-fi设备的分析图；

具体实施方式

本发明针对现有被动式定位技术勘测代价大、应用场景受限的弊端，提出一种面向多重应用的被动式定位方法。主要思路是：利用接收端阵列天线接收信号的相位差来估计目标反射信号的到达角度，进而结合参考阵元的位置对目标进行定位。在商用设备的场景下，设备上采集得到的csi受随机噪声以及发射机与接收机之间的时钟不同步的影响，其原始相位信息很不稳定，本发明试图获取并整合可用的相位信息，计算得到稳定的相位差，使其能够用于可靠的信号到达角度估计。为了实现目标反射信号到达角度估计，进而对目标进行定位，本发明首先利用静止干扰源的角度误差补偿来缓减信号到达角度随时间产生的偏移；其次利用不同种类反射信号之间的相干与非相干性，对环境中移动干扰源和静止干扰源反射信号的到达角度进行消除从而进行目标位置计算，具体步骤介绍如下：

步骤一，在监测区域内部署一个无线信号发送设备，两个无线信号接收设备，三个设备不共线；本实施例中：

在5m*5m的监测区域中部署一个无线信号发送设备，两个无线信号接收设备，我们分别为这两个无线信号接收设备命名为接收端一与接收端二，使得三个设备分布在三角形的三个顶点上，其中发送设备与接收端一和接收端二之间各间隔5m，接收端一与接收端二之间间隔3m，如图6所示。另外，每个接收端上安装一组阵列天线，接收端一上的阵列天线称之为阵列天线一，接收端二上的阵列天线称之为阵列天线二，本实施例中采用的是商用的wi-fi设备，天线数目固定为三根，因此在本方案中阵元数(即阵列天线包含的天线数目)固定为3。

步骤二，在监测区域内没有目标时，两个接收设备同时进行数据的采集，两个接收设备均采集1组发送设备发出的无线信号；最终阵列天线一中的每个阵元与阵列天线二中的每个阵元都得到1组信号，每一组信号包含监测区域内所有信号源的发射信号数据(信号源即为产生反射信号的障碍物或目标)；监测区域内无目标时只有障碍物存在，记接收端一采集无线信号记为情况一，接收端二采集无线信号记为情况二；

当待测目标进入监测区域后(目标进入监测区域的位置是不定的)，两个接收设备均采集r组无线信号；采集持续时间不少于5s，这是由于目标进入监测区域后可能存在移动信源，移动信源发出的信号到达阵列天线的到达角度是会随时间而变化的，而静止信源发出的信号到达阵列天线的到达角度是不会随时间而变化的，这将在步骤五中详细描述，那么我们通过一个短时间内的信号采集就可区别移动信源和静止信源，进而对移动信源进行剔除。最终数据采集结束后阵列天线一中的每个阵元与阵列天线二中的每个阵元都得到r组信号，记此时接收端一采集无线信号记为情况三，接收端二采集无线信号记为情况四。

步骤三，针对上述每一个接收设备在监测区域内有目标、没有目标时采集的无线信号，即上述的情况一至情况四这四种情况下，对每一个接收设备的阵列天线中每一个阵元采集得到的每一组无线信号均进行相位的提取，对提取的相位信息进行线性变换以获取可用的相位特征信息；具体为：

在处理过程中我们设定阵列天线一中的第一个阵元为此阵列天线中的参考阵元，其他阵元为接收阵元，同样我们设定阵列天线二中的第一个阵元为此阵列天线中的参考阵元，其他阵元为接收阵元。按照这样的设定，我们通过上述过程中得到的相位特征信息，用同样的方法分别计算得到4种情况下各个接收阵元上的每一组相位信息相对于参考阵元的相位差。

对于每种情况下，数据处理的方法都是相同的，这里以其中一组信号为例，处理方法的具体实施步骤如下：

一组阵列天线包含m个阵元，m为3，若监测区域中有p个信号源，无目标时只有障碍物存在，相邻两个阵元间隔为d，d小于天线工作波长的一半，第i个信号源发出的信号为si(n)，i＝1,2,…,p；n＝1,2,…,r，在无目标时，我们只采集了一组信号数据，此时r＝1，每一个信号中固定的包含了30个子载波，每一个子载波上都包含了信号的幅度和相位信息；在本文中首先需要对每一组中的每一个信号中的每一个子载波上的相位信息进行提取，其中第w(w＝1,2,…,30)个子载波上的观测相位值ζw可表示为：

公式中：

ψw表示第w个子载波的真实相位值；

δ表示接收端的时钟偏移，

α表示未知的相位偏移量，

χ表示测量噪声。

kw表示第w个子载波的编号(在ieee802.11n中取值在-28到28之间)，

g是快速傅里叶变换采样数(在ieee802.11a/g/n中等于64)

通过公式(1)我们可以得到每一个信号中的每一个子载波上的原始相位信息，但是利用公式(1)得到的相位信息会受到随机噪声的影响，为减少随机噪声的影响，文中在原始相位上执行了一个线性变换，主要通过结合整个频带上的相位，来消除δ和α，因此定义a和b两个变量：

由于子载波频率是对称的，所以则公式(3)可以变形为：

进而，从观测相位ζj中减去线性项akj+b，并忽略掉很小的测量噪声值，即获得了真实相位值的线性组合：

本文将公式(5)所表示的线性组合，作为信号中的每一个子载波真实相位的特征值，从而消除了随机的相位偏移量，图4展示了处理前后的相位分布，可见处理后的相位分布相对稳定集中。

获得真实相位的特征值之后，利用公式(6)可以得到每一个信号到达阵元的真实相位的特征值，

公式(6)中，λi(n)表示第i个信号源发射出的第n个信号到达第u个阵元的真实相位的特征值；

通过公式(6)我们得到了信号真实相位的特征值，将阵列天线中的阵元1作为参考阵元，剩余的阵元为非参考阵元，信号到达其他阵元的时间相对于参考阵元存在延迟，因此信号传播会引起相位差，令信号si(n)电波传播延迟在第2个阵元引起的相位差为τi，则在第3个阵元引起的相位差为2τi，在第u个阵元引起的相位差为(u-1)τi，其中τi为在信号si(n)在第2个阵元上真实相位的特征值与在参考阵元上真实相位的特征值的差值，公式为：

τi＝λ2i(n)-λ1i(n)(7)

通过上述方法的描述，在四种情况下都按照同样的方法对阵列天线各个阵元采集得到每一组信号数据进行处理，分别计算得到每一种情况下各信号达到阵列天线中各非参考阵元相对于参考阵元引起的稳定的相位差。

步骤四，对于每一个接收设备在监测区域内有目标、没有目标时采集的无线信号，即情况一至情况四这四种情况下，分别建立每一个接收设备的阵列天线上所有阵元的信号接收矩阵；

对于前述的四种情况下，信号到达阵列天线，阵列天线中的各个阵元是同时接收数据的，因此阵列天线中的各个阵元接收信号数据的组数是相同的，那么对于每一种情况，我们利用阵列天线中阵元1(参考阵元)、阵元2(接收阵元)、阵元3(接收阵元)上在同一时间接收到的信号数据，建立信号到达阵列天线的所有阵元的信号接收矩阵。

以情况3为例，信号到达阵列天线一，阵列天线一中的各个阵元同时进行数据的采集，在数据采集完成后阵列天线一中的各个阵元分别得到了r组信号数据，此时我们利用各个阵元在同一时间接收到的信号数据，即是提取阵元1、阵元2和阵元3在同一时刻上得到的信号数据，从第一组开始到最后一组(r＝1开始到达结束)，分别建立信号到达阵列天线一所有阵元的信号接收矩阵，具体方法过程如下：

如图2所示，信号si(n)到达各阵元的方向角相同，用θi表示。以阵元1作为参考阵元，信号到达其他接收阵元的时间相对于参考阵元存在延迟。令信号si(n)电波传播延迟在第一个接收阵元引起的相位差为τi，则在第二个接收阵元引起的相位差为2τi，在第m-1个阵元引起的相位差为(m-1)τi。记监测区域内有p个信号源，天线阵列包含m个阵元，则所有信号源发出的信号si(n)到达不同阵元的相位差所组成的向量矩阵可表示为：

上式中：

a(τi)表示第i(i＝1,2...,p)个信号源发出的信号到达m个阵元的相位差所组成的向量；

τi表示信号si(n)电波传播延迟在第一个接收阵元引起的相位差；

j表示虚数单位，m表示阵元数目，e表示自然常数约为2.71878；

设不同阵元上的加性观测噪声为：e(n)＝[e1(n),...,em(n)]^t，其中t表示矩阵转置，ei(n)表示信号到达第i(i＝1,2,...m)个阵元上的加性噪声，m表示阵元总数目，则所有阵元的信号接收矩阵表示为：

上式中：

s(n)＝[s1(n),...,sp(n)]^h(10)

其中h表示转置。

通过步骤四，我们用如上述同样的方法，获得了分别在情况一，情况二，情况三及情况四下的信号接收矩阵。

步骤五，根据步骤四得到的不同信号接收矩阵，得到待测目标进入监测区域后无线信号到达两个接收设备的到达角度，以实现待测目标的定位。

步骤5.1，对于所述的信号接收矩阵，计算其对应的协方差矩阵r；

式中，h为转置，r为阵列天下采集的信号数据组数。

接着，对协方差矩阵r进行特征值分解，得到g个特征值和对应的特征向量；在g个特征值中，有g-p个相等的小的特征值以及p个大的特征值，p为检测区域内的信源个数。下来将p个大的特征值对应的特征向量构成信号子空间us；将小的特征值对应的特征向量构成噪声子空间un，这两个子空间正交；

上式中：

us表示信号子空间；

u1,u2,…,up分别表示与信号对应的p个特征向量；

un表示噪声子空间；

up+1,up+2,…,ug分别表示与噪声对应g-p的个特征向量；

利用公式(14)计算谱函数pmusic(θ)，谱函数中会得到多个峰值，那么峰值个数就是信号源的个数，即是信号源个数p的求解，另外得到的谱函数pmusic(θ)的所有峰值对应的角度便包括每一组信号中p个信号源发出信号到达整个阵列天线的角度估计值θ1,θ2，…,θp，又由于信号到达各阵元的方向角相同，因此这估计得到的角度值也是信号到达各个阵元的角度：

公式中，

pmusic(θ)表示谱函数，

a(θ)表示m个阵元的相位差组成的向量；

un表示噪声子空间；

h表示转置。

在计算谱函数的过程中，θ的范围从0到π，且变化间隔为1度。

通过步骤5.1，我们可以得到每一种情况下，信号中的p个信号源发出的信号到达阵列天线的角度估计值。

步骤5.2.1：区分静止干扰源与除了待测目标之外的其他移动干扰源，并消除移动干扰源，具体为：

目标进入监测区域后，阵列天线一与阵列天线二同时开始数据采集，并采集一小段时间的数据，即为情况三与情况四，两种情况下是同时进行，并且处理方式相同。

以情况三为例，如图5(a)所示，从t_start时刻到t_end时刻，阵列天线一中的各个阵元各得到了r组信号数据，每一组信号数据包括p个信号源，按照步骤一到步骤四中的方法，我们会得到r组角度值，每一组角度值中含有p个信号源到达阵列天线的角度，其中p个信号源含有移动信源和静止信源，在图中移动信源从a点移动到b，在这个时间段内，估计得到的移动信源信号到达角度是变化的，即是得到的r组角度值之中，移动信源到达阵列天线的角度是变化的，而静止信源在这个时间段内，是静止的，因此在得到的r组角度值之中，静止信源的信号到达角度不变，本发明根据信号到达阵列天线的角度是否随时间变换，将静止信源(待测目标信源)和移动信源区分开，具体利用公式(15)来计算信号在不同的时刻到达阵列天线的角度，从而来估计是移动信号源还是静止信号源：

公式中，

是反射信号到达时间；

τ为信号的相位；

f为信号的频率；

a(θ)表示m个阵元的相位差组成的向量；

通过公式(15)我们得知，如果是移动信号源，信号的到达角度在θt_start～θt_end之间变化，如果是静止信号源，信号的到达角度是不变的，综上，通过排除θt_start～θt_end之间的角度，可以消除掉移动干扰源，即剩下所有静止信源的信号到达角度，也就是说得到r组角度中，每一组角度值只剩下静止干扰源和目标信号到达阵列天线的角度，接下来再通过步骤5.2.2来消除静止干扰源，剩下的角度值即为目标信号到达阵列天线的角度。在情况四下处理的方法和上述相同，最终也只会得到目标信号和静止干扰源信号到达阵列天线二的角度。

步骤5.2.2：消除静止干扰源

通过步骤5.2.1我们得到了r组角度值，其中每一组角度值只含有目标信号和静止干扰源信号的到达阵列天线的角度，对于静止干扰源信号我们已经在监测区域中没有目标时，采集得到了信号数据，做为参考信号，此时监测区域中只有静止干扰源，通过步骤一到四的计算，我们就可以得到每一个静止干扰源到达阵列天线的角度，那么情况三以情况一做为参考，情况四以情况二做为参考，最终将步骤5.1.1得到的r组角度值中每一组中的静止干扰源角度值进行剔除，最终就得到r组目标信号到达阵列天线的角度值，具体实施为:

首先将无目标时的两组阵列天线的接收信号矩阵经过正交变换得到的协方差矩阵修正为toeplitz矩阵：

rx＝r+ivr^*iv(16)

上式中：

rx是toeplitz矩阵；

r是接收信号矢量经过正交变换得到的协方差矩阵，具体为：

r^*是r的转置矩阵；

iv是反向单位矩阵，具体为：

接着对对toeplitz矩阵rx进行奇异值分解：

[n,s,u]＝svd(rx)(18)

上式中：

n和v中分别含有rx的奇异向量；

s中含有rx的奇异值；

最后将n作为un带入公式(15)中，估计信号的到达角度，达到的效果如图5(b)和图5(c)所示。进而通过将有目标和无目标情况下的估计结果进行对比即可剔除静止干扰信源信号的到达角度。

步骤5.3：通过步骤5.2，在情况三和情况四下我们分别得到了r组角度值，情况三下每一组角度值中只含有目标信号到达阵列天线一的到达角度，并且这r组角度值是相同的，情况四下每一组角度值中只含有目标信号到达阵列天线二的到达角度，并且这r组角度值是相同的，那么我们就选取r＝1时，目标信号分别到阵列天线一与阵列天线二的到达角度，利用三角测量法确定目标的位置，具体实施为：

根据目标信号到两组阵列天线的到达角度和两个参考阵元的位置关系来进行位置估计，目标与两组阵列天线同处于一个坐标系内，两组阵列天线的坐标(x1,y1)和(x2,y2)已知，两组阵列天线对应的目标信号的到达角度θ1和θ2已知，则有：

则由公式(18)得到目标在监测区域平面内的坐标位置。

实验验证

实验目的

(1)本发明提出的方法是否对商用wi-fi设备和专用设备下采集的电信号分析都有效？

(2)本发明提出的方法是否适用于干扰源分布密集程度不同的环境？

实验环境

本发明选择三种真实场景进行实验：

(1)室外空旷环境，有少量静止干扰物，如图6(a)所示，收发设备的水平高度为1.1m；

(2)室内简单环境，有较多静止干扰物，如图6(b)所示，收发设备的水平高度为1.1m；

(3)室内复杂环境，有大量静止干扰物,如图6(c)所示，收发设备的水平高度为0.75m。

实验设备

未验证本发明提出方法的通用性，本发明分别在商用wi-fi设备和专用的usrp实验平台下进行实验。

商用设备：发射端为现有的wlan设备(tl-wr2041n300m三天线无线路由器)，接收端使用intel5300网卡(有三根接收天线，增益为3dbi)。

专用设备：发射端用北京海曼公司开发的usrp，产生频率为2488mhz的无线电信号(正弦信号)，发射天线(型号wa5vjb)为850mhz至6.5ghz的对数周期定向天线，增益为5-6dbi。接收端用四天线阵列和示波器相连，接收天线工作频率为2.4ghz全向天线，增益为3dbi。

实验一

实验一的目标在于验证本发明的有效性。将本发明中的方法分别在两种不同实验平台与三种真实实验场景环境下的定位精度与传统的两种方法rass和lcs进行对比，为方便将该方法在usrp和wi-fi平台上实现记为maloc1和maloc2。

实验一的测试结果：

如图7所示，随着环境的逐步复杂化，四种定位方法的精度逐步降低(中值误差大约由0.75m到1m,再到1.5m左右变化)，并且本发明方法的精度略高于传统方法的精度，逐步变化到向传统方法的精度靠拢,除此之外，还可以看出本文定位模型在两种不同实验平台下的定位误差基本相近，可见本文对商用设备下的信号不稳定相位进行处理对保证定位精度起到了关键性的作用,综上充分表明了本发明中所提及方法的有效性。

实验二

实验二的目标在于研究接收端个数和移动干扰目标个数对定位精度的影响。本发明通过两个扩展实验对此进行分析，1)移动干扰目标个数取默认值1，将接收端个数从2增加到5；2)接收端个数取默认值2，将移动干扰目标个数从1增加到4。

实验二的测试结果：

如图8所示。定位精度随着环境的复杂化逐渐降低。本发明在专用usrp下的定位精度要高于在商用wi-fi设备下的定位精度，但是相差不超过0.25m，可见本文对商用设备下的不稳定相位进行处理有效提高了其定位性能。对比后发现，随着接收端个数增加，定位精度提高，可见结合多次定位的结果可有效缓解因某次定位偏差大(比如测量盲点)导致整体定位精度降低的问题。而随着环境中移动干扰目标个数的增加，定位精度降低，此结果是由于移动干扰目标出现会导致接收端对目标反射信号的到达角度分辨能力减弱，最终导致定位精度降低。

实验三

实验三的目标在于对到达角度估计误差分析，在不同实验平台下，不同实验场景环境下对得到的目标反射信号进行对比。

实验三的测试结果

如图9所示。环境越复杂，到达角度与距离的估计误差越大。其中，在专用usrp平台下，三种场景下的到达角度估计的中值误差分别为8°，10.05°和12.5°。在商用wi-fi平台下，三种场景下的到达角度估计的中值误差分别为10.4°，12.6°和13.79°。两种平台下的到达角度估计误差相差甚微。由此可见，本发明对商用设备下采集的信号相位校准方法有效缓解了原始相位不稳定性带来的影响。