用于模态匹配状态硅微机械陀螺仪带宽拓展数字校正方法与流程
本发明涉及硅微机械陀螺仪,具体是一种用于模态匹配状态硅微机械陀螺仪带宽拓展数字校正方法。
背景技术:
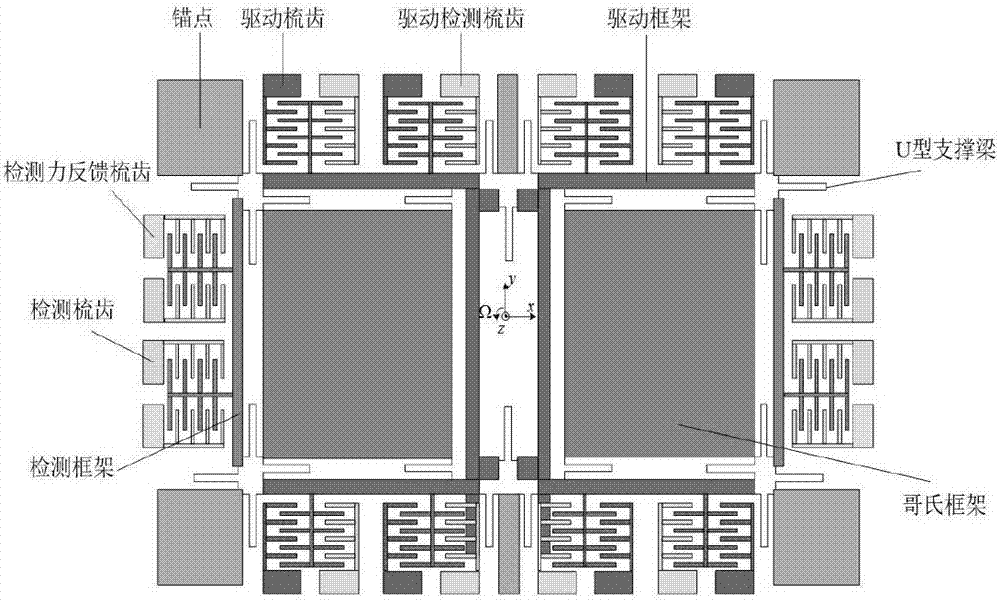
硅微机械陀螺仪是指利用微机电系统(mems)技术,并根据哥氏效应原理工作的一类用于测量角速度的惯性传感器。其具有体积小、重量轻、低功耗、低成本、易于批量化生产、集成度高、易于数字化等特点,已经在民用领域(如手机、平板电脑、数码相机等消费类电子)和军用领域(如制导弹药、战场机器人、军用无人机等)有着广泛的应用。如图1和如图2所示,硅微机械陀螺仪包括陀螺微结构和陀螺测控电路。所述陀螺结构由驱动框架、检测框架、哥氏框架、驱动梳齿、驱动检测梳齿、检测梳齿、检测反馈梳齿、u型支撑梁及基座等组成。在u型梁的作用下,驱动框架只能沿x轴方向运动,检测框架只能沿y轴方向运动,哥氏框架可以同时沿x轴方向和y轴方向运动。陀螺正常工作时,在静电驱动力作用下,驱动框架和哥氏框架一起沿x轴方向作等幅反向运动;当陀螺有绕z轴的角速度输入时,检测框架和哥氏框架在哥氏力的作用下,沿y轴作等幅反向运动。所述陀螺测控电路包括高性能c/v接口电路,ad/da转换模块以及fpga处理模块。其中,fpga数字平台是该控制系统的核心模块,驱动模态和检测模态的控制及有效输出均由此控制。闭环驱动回路为陀螺检测回路提供稳定的振动位移,当有z轴方向角速度输入时,根据哥氏效应,将在检测方向产生振动,通过检测陀螺检测模态产生的振动位移就可以得到输入角速度的大小。陀螺检测模态的工作方式可以分为开环检测和闭环检测。开环检测工作方式下,陀螺输出的检测位移幅度与输入角速度成比例关系,经过解调输出的电压直接反映角速度信息。闭环检测工作方式需在陀螺检测模态添加力反馈检测电极,通过检测力反馈闭环控制回路,使检测反馈力与哥氏力抵消,保证陀螺检测梳齿始终保持在平衡位置,通过反馈力的大小来得到角速度信息。
如图3所示,硅微机械陀螺仪开环检测的工作原理,采用常用的乘法相敏解调提取哥氏信号。图中,ωz(t)表示输入角速度,my为陀螺检测模态检测质量,ax为驱动梳齿振动位移,ωd为驱动角频率,fc为哥氏力,gy(s)为陀螺检测模态传递函数,y(t)为陀螺检测模态输出位移,kyc为检测模态梳齿电容转换增益,kcv为电容电压转换增益,kamp为检测回路前置放大器增益,vref为解调基准电压,
陀螺检测模态传递函数的表达式为:
式(a1)中:gy(s)为陀螺检测模态传递函数,my为陀螺检测模态检测质量,ωy为检测模态谐振频率,qy为检测模态品质因数。
根据开环检测工作原理,可以得到角速度检测开环传递函数为:
式(a2)中:hopen(s)为陀螺检测开环传递函数,vopen为硅微机械陀螺仪开环检测输出电压,ωz表示输入角速度,kyc为检测模态梳齿电容转换增益,kcv为电容电压转换增益,kamp为检测回路前置放大器增益,vref为解调基准电压,ax为驱动梳齿振动位移,ωd为驱动角频率,flpf(s)为相敏解调环节中的低通滤波器传递函数,
对于模态匹配工作方式的硅微机械陀螺仪,即ωy=ωx=ωd,此时理想解调相位
式(a3)中:
从式(a3)可以发现,当陀螺处于模态匹配状态时,不考虑后级低通滤波器环节的情况下,开环检测传递函数类似为一个截止频率为
对于模态匹配工作方式的硅微机械陀螺仪,根据式(a3)得到静态灵敏度为:
式(a4)中,
从式(a4)可知,陀螺模态匹配工作模式下的开环检测灵敏度与检测模态梳齿电容检测增益、前端电路放大增益、解调基准幅度、驱动振幅、检测模态品质因数以及谐振频率有关。增大开环检测增益、增加驱动模态振动幅度ax、提高检测模态品质因数qy以及减小检测模态谐振频率ωy均可提高硅微机械陀螺仪静态灵敏度。
根据带宽的定义,开环系统幅频特性相对于频率为零时下降3db对应的频率点即为陀螺的工作带宽。即满足等式:
式(a5)中:hopen(s)为陀螺开环检测传递函数,ωb为陀螺工作带宽。
对于模态匹配的硅微机械陀螺仪,由于开环检测传递函数类似为一阶低通滤波器,因此,带宽由式(a5)得:
式(a6)中:ωb为陀螺工作带宽,ωy为硅微机械陀螺仪检测模态的谐振角频率,qy为检测模态品质因数。
一般硅微机械陀螺仪检测模态品质因数在几百量级,谐振频率在几千量级,因此,模态匹配状态的硅微机械陀螺仪开环检测下的工作带宽只有几赫兹。
从陀螺开环检测系统的工作带宽和静态灵敏度可知,模态匹配状态下的硅微机械陀螺仪是牺牲带宽来换取高灵敏度,二者在开环检测模式下是个矛盾的关系,为了同时兼顾带宽和灵敏度,必须发明一种全新的方法,以解决模态匹配状态下硅微机械陀螺仪无法兼顾静态灵敏度和工作带宽的问题。
技术实现要素:
发明目的:为了克服现有技术中存在的不足,本发明提供一种用于模态匹配状态硅微机械陀螺仪带宽拓展数字校正方法。
技术方案:为解决上述技术问题,本发明的一种用于模态匹配状态硅微机械陀螺仪带宽拓展数字校正方法,包括以下步骤:
1)对开环检测进行改进,构成陀螺闭环检测环路,根据闭环检测工作原理,可以得到角速度检测闭环传递函数为:
式(a7)中:hclose(s)为陀螺检测闭环传递函数,vclose为硅微机械陀螺仪闭环检测输出电压,ωz表示输入角速度,my为陀螺检测模态检测质量,ax为驱动梳齿振动位移,hopen(s)为陀螺检测开环传递函数,kyvf为反馈电压到检测反馈力的转换系数,kyc为检测模态梳齿电容转换增益,kcv为电容电压转换增益,kamp为检测回路前置放大器增益,vref为解调基准电压,
闭环检测系统的静态灵敏度可以表示为:
式(a8)中:ks为硅微机械陀螺仪闭环检测静态灵敏度,hclose(s)为陀螺检测闭环传递函数,my为陀螺检测模态检测质量,ax为驱动梳齿振动位移,hopen(s)为陀螺检测开环传递函数,kyvf为反馈电压到检测反馈力的转换系数,kyc为检测模态梳齿电容转换增益,kcv为电容电压转换增益,kamp为检测回路前置放大器增益,vref为解调基准电压,
当校正器静态增益ffb(0)很大,即满足环路增益>>1时,此时有:
式(a9)中:ks为硅微机械陀螺仪闭环检测静态灵敏度,my为陀螺检测模态检测质量,ax为驱动梳齿振动位移,ωd为驱动角频率,kyvf为反馈电压到检测反馈力的转换系数;
从式(a9)可以发现,当环路增益很大时,检测闭环控制系统的静态灵敏度与陀螺频差无关,也与前馈检测增益无关;只与检测质量块大小、驱动模态振动幅度和谐振频率以及检测力反馈转换增益有关;比较式(a9)和式(a4)可知,与开环检测系统的静态灵敏度相比,闭环检测系统的静态灵敏度受温度等环境影响较小,因此可以显著改善系统的稳定性和可靠性;
2)为了方便设计闭环校正器,从哥氏力输入和反馈力输出的角度构成单位负反馈系统,该闭环反馈系统的开环传递函数为:
式(a10)中:hopen(s)表示闭环反馈系统的开环传递函数,ff为检测反馈力,ωz表示输入角速度,kyc为检测模态梳齿电容转换增益,kcv为电容电压转换增益,kamp为检测回路前置放大器增益,vref为解调基准电压,ax为驱动梳齿振动位移,ωd为驱动角频率,flpf(s)为低通滤波器传递函数,ffb(s)为力反馈校正器传递函数,kyvf为反馈电压到检测反馈力的转换系数,
在系统中加入频率特性合适的校正器,应该使开环系统频率特性形状满足:低频段增益充分大,以保证系统稳态误差的要求;中频段对数幅频特性斜率-20db/dec,并占据充分宽的频带,以保证系统具备适当的相角裕度;高频段增益应尽快减小,以削弱噪声的影响;由于模态匹配状态下的陀螺检测模型可以看作一阶惯性环节,因此,可以采用pi环节与相位超前环节相结合的串联校正方式来对检测控制回路进行整形;
校正器的传递函数为:
式(a11)中:ffb(s)为力反馈校正器传递函数,kp、ki分别为比例积分控制器的比例系数和积分系数,ω1和ω2分别为相位超前环节的零极点,且ω1<ω2;
3)由于硅微机械陀螺仪实际控制系统中的校正器由数字电路实现,因此,需要对式(a11)进行离散域变换,比例积分控制器的离散域模型为:
式(a12)中:d1(z)为比例积分控制器的离散域表达式,kp、ki分别为比例积分控制器的比例系数和积分系数,t0为离散系统采样间隔;
相位超前环节的离散模型利用双线性变换法得:
式(a13)中:d2(z)为相位超前环节的离散域表达式,ω1和ω2分别为相位超前环节的零极点,t0为离散系统采样间隔;
因此,所发明的比例积分控制器与相位超前环节串联数字校正器的表达式为:
式(a14)中:d(z)为所发明的数字校正器,d1(z)为比例积分控制器的离散域表达式,d2(z)为相位超前环节的离散域表达式,kp、ki分别为比例积分控制器的比例系数和积分系数,ω1、ω2分别为相位超前环节的零极点,t0为离散系统采样间隔。
有益效果:本发明的一种用于模态匹配状态硅微机械陀螺仪带宽拓展数字校正方法,具有以下有益效果:
通过构建闭环检测环路,用所发明的数字校正器对检测控制回路进行整形,从而使得硅微机械陀螺仪静态灵敏度与工作带宽不再矛盾,进而使得硅微机械陀螺仪能够同时兼顾静态灵敏度和工作带宽。本发明有效解决了模态匹配状态硅微机械陀螺仪无法兼顾静态灵敏度和工作带宽的问题,适用于模态匹配状态的硅微机械陀螺仪。
附图说明
图1为本发明的硅微机械陀螺仪的结构示意图;
图2为本发明的硅微机械陀螺仪的测控电路系统框图;
图3为本发明的硅微机械陀螺仪开环检测工作原理框图;
图4为本发明的硅微机械陀螺仪闭环检测工作原理框图;
图5为本发明的硅微机械陀螺仪闭环检测回路单位负反馈系统框图;
图6为本发明的比例积分相位超前数字校正器结构示意图;
图7为本发明的校正器的伯德图;
其中,图7a为由式(a11)所示的连续域校正器得到的幅频特性曲线图和相频特性曲线图;
图7b为由式(a14)所示的数字域校正器得到幅频特性曲线图和相频特性曲线图。
具体实施方式
下面结合附图对本发明作进一步说明。
本发明提供了一种用于模态匹配状态硅微机械陀螺仪带宽拓展数字校正方法,该方法是采用如下步骤实现的:
1)对开环检测进行改进,原理框图如图4所示,构成陀螺闭环检测环路,图中,ωz(t)表示输入角速度,my为陀螺检测模态检测质量,ax为驱动梳齿振动位移,ωd为驱动角频率,fc为哥氏力,gy(s)为陀螺检测模态传递函数,y(t)为陀螺检测模态输出位移,kyc为检测模态梳齿电容转换增益,kcv为电容电压转换增益,kamp为检测回路前置放大器增益,vref为解调基准电压,
根据闭环检测工作原理,可以得到角速度检测闭环传递函数为:
式(a7)中:hclose(s)为陀螺检测闭环传递函数,vclose为硅微机械陀螺仪闭环检测输出电压,ωz表示输入角速度,my为陀螺检测模态检测质量,ax为驱动梳齿振动位移,hopen(s)为陀螺检测开环传递函数,kyvf为反馈电压到检测反馈力的转换系数,kyc为检测模态梳齿电容转换增益,kcv为电容电压转换增益,kamp为检测回路前置放大器增益,vref为解调基准电压,
闭环检测系统的静态灵敏度可以表示为:
式(a8)中:ks为硅微机械陀螺仪闭环检测静态灵敏度,hclose(s)为陀螺检测闭环传递函数,my为陀螺检测模态检测质量,ax为驱动梳齿振动位移,hopen(s)为陀螺检测开环传递函数,kyvf为反馈电压到检测反馈力的转换系数,kyc为检测模态梳齿电容转换增益,kcv为电容电压转换增益,kamp为检测回路前置放大器增益,vref为解调基准电压,
当校正器静态增益ffb(0)很大,即满足环路增益>>1时,此时有:
式(a9)中:ks为硅微机械陀螺仪闭环检测静态灵敏度,my为陀螺检测模态检测质量,ax为驱动梳齿振动位移,ωd为驱动角频率,kyvf为反馈电压到检测反馈力的转换系数。
从式(a9)可以发现,当环路增益很大时,检测闭环控制系统的静态灵敏度与陀螺频差无关,也与前馈检测增益无关;只与检测质量块大小、驱动模态振动幅度和谐振频率以及检测力反馈转换增益有关。比较式(a9)和式(a4)可知,与开环检测系统的静态灵敏度相比,闭环检测系统的静态灵敏度受温度等环境影响较小,因此可以显著改善系统的稳定性和可靠性。
2)为了方便设计闭环校正器,对图4进行简化,从哥氏力输入和反馈力输出的角度构成单位负反馈系统,如图5所示。图中,该闭环反馈系统的开环传递函数为:
式(a10)中:hopen(s)表示闭环反馈系统的开环传递函数,ff为检测反馈力,ωz表示输入角速度,kyc为检测模态梳齿电容转换增益,kcv为电容电压转换增益,kamp为检测回路前置放大器增益,vref为解调基准电压,ax为驱动梳齿振动位移,ωd为驱动角频率,flpf(s)为低通滤波器传递函数,ffb(s)为力反馈校正器传递函数,kyvf为反馈电压到检测反馈力的转换系数,
当环路增益很大时,检测闭环控制系统的静态灵敏度只与反馈增益有关,与前馈增益无关,受温度等环境影响较小。但是单纯的增大校正器增益无法满足闭环系统稳定性和动态性的要求,因此需要对检测力反馈校正器进行详细设计。在闭环检测系统中加入校正器的目的主要有如下几点:增大开环增益、拓展系统的带宽、增大系统幅值裕度、保证系统相角裕度、保持低频段增益的平坦以及带宽满足后幅度应迅速衰减等。
在系统中加入频率特性合适的校正器,应该使开环系统频率特性形状满足:低频段增益充分大,以保证系统稳态误差的要求;中频段对数幅频特性斜率-20db/dec,并占据充分宽的频带,以保证系统具备适当的相角裕度;高频段增益应尽快减小,以削弱噪声的影响。由于模态匹配状态下的陀螺检测模型可以看作一阶惯性环节,因此,可以采用比例积分环节与相位超前环节相结合的串联校正方式来对检测控制回路进行整形。
校正器的传递函数为:
式(a11)中:ffb(s)为力反馈校正器传递函数,kp、ki分别为比例积分控制器的比例系数和积分系数,ω1和ω2分别为相位超前环节的零极点,且ω1<ω2。
3)由于硅微机械陀螺仪实际控制系统中的校正器由数字电路实现,因此,需要对式(a11)进行离散域变换,比例积分控制器的离散域模型为:
式(a12)中:d1(z)为比例积分控制器的离散域表达式,kp、ki分别为比例积分控制器的比例系数和积分系数,t0为离散系统采样间隔。
相位超前环节的离散模型利用双线性变换法得:
式(a13)中:d2(z)为相位超前环节的离散域表达式,ω1和ω2分别为相位超前环节的零极点,t0为离散系统采样间隔。
因此,所发明的比例积分控制器与相位超前环节串联数字校正器的表达式为:
式(a14)中:d(z)为所发明的数字校正器,d1(z)为比例积分控制器的离散域表达式,d2(z)为相位超前环节的离散域表达式,kp、ki分别为比例积分控制器的比例系数和积分系数,ω1、ω2分别为相位超前环节的零极点,t0为离散系统采样间隔。
图6为本发明的比例积分相位超前数字校正器结构示意图,由比例积分控制器和相位超前环节串联组成,数字校正器的表达式如式(a14)所示;
根据式(a14)得到的伯德图如图7a,7b所示,并将式(a11)的频率特性曲线绘制在图7中。从图可以发现离散域校正器的频率特性曲线与连续域校正器的基本一致,因此,可以用数字校正器(a14)代替式(a11)构成模态匹配状态硅微机械陀螺仪闭环检测系统。其中,图7a的幅频特性曲线图和相频特性曲线图中的两条曲线由式(a11)所示的连续域校正器得到,图7b幅频特性曲线图和相频特性曲线图中的两条曲线由式(a14)所示的数字域校正器得到。
以上所述仅是本发明的优选实施方式,应当指出:对于本技术领域的普通技术人员来说,在不脱离本发明原理的前提下,还可以做出若干改进和润饰,这些改进和润饰也应视为本发明的保护范围。
- 还没有人留言评论。精彩留言会获得点赞!