一种光吸收系数测量装置及方法与流程

本发明属于光学计量领域，主要涉及一种光吸收系数测量方法，尤其涉及一种低吸系数光学元件的光吸收系数测量装置及方法。

背景技术：

随着高功率激光系统在受控热核反应、核爆模拟、高能激光武器等尖端技术的应用，使得大口径、低吸收系数激光光学元件的研制和检测技术进入了一个新的阶段，上述光学元件通常口径在400mm量级，而吸收系数低至10^-4cm^-1量级。光吸收系数是评价此类光学元件的重要参数，直接决定光学元件的损伤阈值和应用过程中对光束质量的影响。

精确测量光学元件吸收系数的方法主要有量热法、光声技术测量法和透射法。量热法是将被测样品置于真空状态的卡计室，使样品处于绝缘状态，利用单一波长的激光通过该介质后，测量样品温度和时间变化关系给出吸收系数；这种测量方法灵敏度很高，精度可达到10^-5cm^-1，但是受真空卡计室的测试条件限制，无法对大口径光学材料进行测量。光声技术测量法将样品放置在光声池中，用连续或脉冲光束入射至样品，随后样品的温度上升通过测量气室压力增加得到，另外也可以通过使用附着于样品上的传感器测量光声效应导致的弹性波振幅，或者使用置于光声池中的超声探测器探测样品产生的脉冲光声信号来计算被测样品的光吸收系数；这种测试方法需要建立精确数学模型，需要特殊的实验环境和条件，测量精度受很多因素影响，在工程上应用受到限制，同时很难测量大口径光学材料的吸收系数。透射法是行业标准jb/t9495.6-1999《光学晶体吸收系数测量方法》中采用的方法，此方法采用垂直入射测量被测样品的透过率，然后结合样品的折射率通过计算得到样品的吸收系数，这种方法的局限性在于如果光源为激光，在垂直入射经过两面平行度较好的材料时，多次透射光的频率相同、振动方向相同、相位差恒定，透射光会发生干涉，透射光强发生波动，影响测试结果，已经无法满足现有技术环境下10^-4cm^-1的精度要求，此外这种测量方法是对白光的吸收系数进行测量，无法测量被测样品对特定波长、特定偏振态激光的吸收系数。

同时，对于目前使用最为广泛的单轴晶体材料，偏振光进入后分解为o光和e光，不同入射角度的o光在材料中传输时，晶体折射率不会发生变化，但是对于e光，其吸收系数与晶体的折射率和入射角有关，即对于o光和e光，单轴晶体会表现出不同的吸收系数，上述方法都无法给出单独针对o光和e光的吸收系数。

目前，对于大口径、低吸收系数的光学材料，尚未有精确的吸收系数测量方法。

技术实现要素：

为解决上述背景技术中提出的现有方法存在的问题，本发明提出了一种光吸收系数测量装置及方法，能够解决低吸系数光学元件的光吸收系数测量问题。

本发明的技术方案为：

所述一种光吸收系数测量装置，其特征在于：由光源、移动平台、探测器和装有吸收系数测试程序的计算机组成；

所述光源提供时间稳定性优于5×10^-5的线偏振激光，并且能够提供p偏振态的激光和/或s偏振态的激光；

所述移动平台能够固定被测样品并使其移动；

所述探测器探测范围与光源发出的线偏振光的强度范围适应；探测器的探测值传输给装有吸收系数测试程序的计算机。

进一步的优选方案，所述一种光吸收系数测量装置，其特征在于：装有吸收系数测试程序的计算机中存储有光源稳定性阈值a，光源向被测样品发出激光的入射角θ，探测器的探测间隔时间t，探测值个数j，自然常数e，光速c，被测样品的类型，所述类型为各向同性晶体或单轴晶体；如果被测样品为各向同性晶体，则还存储其折射率n；如果被测样品为单轴晶体，则还存储其o光的折射率no、e光的主射率ne，以及晶角α。

所述一种光吸收系数测量方法，其特征在于：包括以下步骤：

步骤1：对测量装置上电并初始化；

步骤2：对光源进行采样：

移动平台带动被测样品移开光路，用探测器探测光源发出的光，每隔时间t进行一次探测，总共探测j个值，并将探测值v1、v2、v3……vj传输给计算机，计算机将所述探测值转化为光源的实际光强值i1、i2、i3……ij；

步骤3：判断光源是否已经稳定：

若步骤2得到的j个实际光强值均满足以下公式

则判定光源稳定，其中a为光源稳定性阈值；并根据公式

计算当前光强值i均；

步骤4：移动平台带动被测样品移入光路，用探测器探测第一次透射光，每隔时间t1进行一次探测，总共探测j1个值，取这j1个值的均值为第一次透射光光强t1，

步骤5：根据被测样品类型，分别采用以下两种步骤进行，若被测样品为各向同性的晶体则进入步骤6，如果被测样品为单轴晶体，则进入步骤7；

步骤6：根据

计算被测样品的吸收系数k；其中l为激光在被测样品中入射点与第一次透射点的传播距离；ρ(θ)为反射率：

θ为光源向被测样品发出激光的入射角，θ'为折射角；n空sinθ＝nsinθ'，n空为空气折射率，n为各向同性晶体被测样品折射率；

步骤7：分别计算单轴晶体对o光和e光的吸收系数：

步骤7.1：调整光源，使其出射光的偏振态为s偏振态，激光的振动方向与水平方向垂直，被测样品晶面法线水平，激光进入被测样品后为o光；根据步骤3计算i均，根据步骤4计算第一次透射光光强t1，根据

计算得到单轴晶体对o光的吸收系数；

θ为光源向被测样品发出激光的入射角，θ'为折射角；n空sinθ＝nosinθ'，n空为空气折射率，no为单轴晶体对o光的折射率；

步骤7.2：调整光源，使其出射光的偏振态为p偏振态，激光的振动方向与入射面平行，被测样品晶面法线水平，激光进入被测样品后为e光；根据步骤3计算i均，根据步骤4计算第一次透射光光强t1，根据

计算得到单轴晶体对e光的吸收系数；

θ为光源向被测样品发出激光的入射角，θ'为折射角；n空sinθ＝ne(θ)sinθ'，n空为空气折射率，ne(θ)为单轴晶体对e光的折射率；

步骤7.3：通过以下迭代计算得到单轴晶体对e光的折射角θ'：

对于第x次迭代，得到单轴晶体对e光的折射角θ'x为

ve(θ′)x＝vo²cos²ψx+ve²sin²ψx

ψx＝90°－θ'x-1－α

其中θ'x-1为第x-1次迭代得到的单轴晶体对e光的折射角，c为光速，α为晶角，vo为o光在被测样品中的传播速度，ne为当e光垂直光轴入射时的主折射率；单轴晶体对e光的折射角的初始值取入射角θ。

进一步的优选方案，所述一种光吸收系数测量方法，其特征在于：步骤2中，探测间隔时间t的值取1秒，探测值个数j取180。

进一步的优选方案，所述一种光吸收系数测量方法，其特征在于：光源稳定性阈值a取0.1％。

进一步的优选方案，所述一种光吸收系数测量方法，其特征在于：步骤4中t1取0.1秒，j1取50。

有益效果

本发明的整体技术效果体现在：选用角度θ的斜入射方式测试样品的吸收系数，避免了透射光干涉造成光强波动带来的不确定度，提高了测试精度；针对单光轴晶体，对o光和e光的吸收系数分别考察，保证了吸收系数测量结果的科学性，选用可产生p偏振态或s偏振态激光的光源，保证在测试时通过晶体的仅为e光或仅为o光，大大方便了测试和计算，保证了测试的精度；选用迭代算法，并选择合适的迭代次数计算获得e光的折射角，既保证了精度，又优化了测试的过程；最后，本发明在普通实验室条件下进行，不需要特殊的实验环境和复杂的实验装置，便于实施。

附图说明

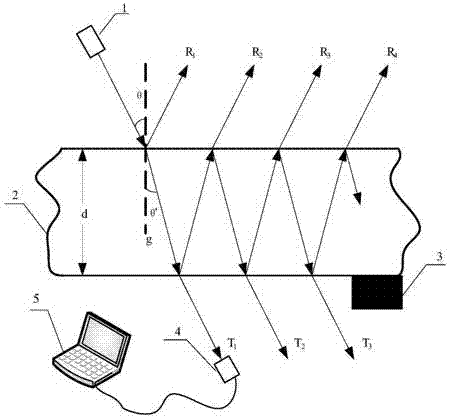
图1是本发明的光路原理图。

图2是被测样品中的e光折射原理图。

具体实施方式

下面结合附图及优选实施例对本发明作进一步的详述。

如图1所示，本发明的一种优选实施例包含光源1，被测样品2，移动平台3，探测器4和装有吸收系数测试程序的计算机5。

光源1中带有起偏/检偏器和半波片，提供时间稳定性优于5×10^-5的线偏振激光，在测试中还能够提供p偏振态的光或s偏振态的激光；被测样品2为厚度均匀、形状任意的被测的大口径、低吸收系数的光学材料，被测样品2的材质可以是普通各向同性光学材料，也可以是单轴晶体材料，由于大口径、低吸收系数的光学材料一般不采用多轴晶体材料，所以本发明只考虑普通各向同性光学材料和单轴晶体材料，被测样品2下文简称样品2，其厚度记为d，厚度为d的两个相对面称为晶面，g表示样品2晶面的法线，θ表示入射角，θ'表示折射角；移动平台3可以固定被测样品2并使其移动；探测器4选用光电探测器，能够精确探测光信号，其探测范围与光源1发出的线偏振光的强度范围相适应，探测器4的探测值通过数据线传输给计算机5；计算机5中预存有光源稳定性阈值a，入射角θ，探测间隔时间t，探测值个数j，自然常数e，光速c，样品2的类型(各向同性晶体或单轴晶体)，如果样品2为各向同性晶体，则存储其折射率n，如果样品2为单轴晶体，则存储其o光的折射率no、e光的主射率ne，并存储光轴与晶面的夹角，即晶角α；吸收系数测试程序能将所述探测器4的探测值对应转化为光源1的实际光强值，控制模块可以控制所述移动平台3运动，显示模块可以显示吸收系数测量结果。

光源1发出的光入射到样品2的晶面上，样品2固定在移动平台3上，并保持法线g与水平面平行，为方便后续的测试和计算，如果样品2为单轴晶体，需保持其光轴与水平面平行；移动平台3带动样品2移开光路时，光源1发出的光由探测器4接收；样品2未移出光路时，光源1发出的光与法线g呈角度θ入射到样品2晶面，在该晶面发生反射和折射，同样，从光线从样品2进入到空气中时，在相对的另一个晶面也会发生反射和折射，如图1所示，r1、r2、r3、r4依次为第一次反射光、第二次反射光、第三次反射光、第四次反射光，t1、t2、t3依次为第一次透射光、第二次透射光、第三次透射光。

所述入射角θ的选择受样品2的厚度限制。光线穿过样品2后会有t1、t2、t3等多次透射光，这几束透射光的空间距离比较近，给后续测试中单独探测透射光t1带来较多不便，在样品2的厚度一定的情况下，入射角θ越大，t1、t2、t3之间的空间距离越大，单独探测t1越方便，但同时反射光r1、r2、r3、r4等也越强，不利于测试；本实施例中入射角θ的角度选为5°。

实施本发明的典型步骤如下：

步骤1：对测量装置上电并初始化。

步骤2：对光源进行采样：

移动平台3带动样品2移开光路，用探测器4探测光源1发出的光，每隔时间t进行一次探测，总共探测j个值，并将这一系列探测值v1、v2、v3……vj传输给计算机5，计算机5将所述探测值转化为光源1的实际光强值i1、i2、i3……ij，探测间隔时间t和探测值个数j的取值由光源1的稳定性和具体实验要求决定，光源1的稳定性越好，探测间隔时间t取的越大，探测值个数j取的越少，具体实验对光源稳定性要求越高，探测间隔时间t取的越小，探测值个数j取的越大；一般情况下探测间隔时间t的值取1秒，探测值个数j取180。

步骤3：判断光源是否已经稳定：

判定光源1发出的光是否稳定性优于光源稳定性阈值a，即判定是否有公式1成立，如果公式1不成立，返回步骤2，重新探测，如果公式1成立，说明光源已经稳定工作，根据公式2计算i1、i2、i3……ij的均值i均作为当前光强值，并进入步骤4；

光源稳定性阈值a在不影响实验结果的情况下取的越大越方便实验进行，本实施例取值为0.1％。

步骤4：探测第一次透射光：

移动平台3带动样品2移入光路，用探测器4探测第一次透射光，每隔时间t1进行一次探测，总共探测j1个值，取这j1个值的均值为第一次透射光光强t1，即

本实施例中t1取0.1秒，j1取50。

步骤5：根据被测样品类型，分别采用以下两种步骤进行，若被测样品为各向同性的晶体则进入步骤6，如果被测样品为单轴晶体，则进入步骤7。

步骤6：计算各向同性晶体的吸收系数：

根据比尔－朗伯定律，当光在一种介质内传播时，光强随着光波在介质内传播距离l的增大按指数规律衰减，则传播中的光强i光与所述传播距离l符合公式3：

i光＝i初e^-kl公式3

其中，i初表示初始入射光强，此处取i初＝i均，第一次透射光光强t1在晶体中的传播距离l利用计算4计算。

l＝d/cosθ'公式4

其中θ'为折射角，根据折射定律，取空气折射率n空为1，折射角满足公式5

n空sinθ＝nsinθ'公式5

如图1，样品2表面的第一次反射光r1＝ρ(θ)i均，其中ρ(θ)是反射率，根据菲涅尔公式可以得到，ρ(θ)与入射角θ和折射角θ'满足以下公式：

进入介质的折射光的光强为i均-ρ(θ)i均＝(1-ρ(θ))i均，根据公式3，光波在材料内部传播时发生指数衰减，到达材料下表面时的光强为(1-ρ(θ))i均e^-kl，在下表面再次发生反射和折射，第一次透射光t1＝(1-ρ(θ))²i均e^-kl，

因此吸收系数k可由公式7计算：

联立公式4、公式5、公式6、公式7计算出样品2的吸收系数k。

步骤7：计算单轴晶体的吸收系数：

对于单轴晶体，偏振光进入后分解为o光和e光，不同入射角度的o光在材料中传输时，晶体折射率不会发生变化，但是对于e光，其折射率与晶体的折射率和入射角θ有关，所以对于o光和e光，单轴晶体会表现出不同的吸收系数，需要分别计算。

步骤7.1：计算o光吸收系数：

调整光源1，使其出射光的偏振态为s偏振态，激光的振动方向与水平方向垂直，因此该激光的振动方向与光轴垂直，进入样品2后为o光。

利用步骤3的方法计算i均，利用步骤4的方法得到第一次透射光光强t1。

取空气中的折射率为1，根据折射定律，o光的折射角θ′满足公式8：

sinθ＝nosinθ′公式8

利用公式4、公式6，公式7和公式8计算吸收系数k，即为o光的吸收系数。

将o光的吸收系数显示在计算机屏幕上。

步骤7.2：计算e光的吸收系数：

通过调整光源1，使其出射光的偏振态为p偏振态，激光的振动方向与入射面平行，显然此激光的振动方向与光轴平行，该激光进入样品2后是e光。

利用步骤3的方法计算i均，利用步骤4的方法得到第一次透射光光强t1。

对于e光，根据菲涅耳公式，入射光的反射率ρ(θ)满足公式9：

取空气中的折射率为1，根据折射定律，e光的折射角θ′和样品2对e光的折射率ne(θ)满足公式10：

sinθ＝ne(θ)sinθ'公式10

其中，折射率ne(θ)随角度θ的变化而变化，无法由公式10直接计算折射角θ'。

以下介绍用迭代的方法计算e光折射角θ'。

步骤i，理论准备

o光在样品2中的传播速度vo是固定的，且满足而e光在样品2中的传播速度ve(θ)与入射角θ有关，并满足公式11

当e光垂直光轴入射时，折射率ne(θ)即为主折射率ne，此时ve(θ)取得极值ve，即

如图2所示，α是样品2的晶角，ψ是e光入射样品2后折射光与光轴的夹角，所以有公式12成立；

ψ＝90°-θ'-α公式12

根据“马科斯·波恩”等的著作《光学原理》(第七版下册第675页)，可以得到ve(θ')的如下计算公式13，

步骤ii，迭代计算

第一次迭代：设折射角θ'的初始值为θ，代入公式12，可以得到ψ的第一次迭代值ψ1，即

ψ1＝90°－θ－α

将ψ1代入公式13，得到ve(θ')的第一次迭代值ve(θ')1，即

ve(θ′)1＝vo²cos²ψ1+ve²sin²ψ1

由公式11可以计算ne(θ')的第一次迭代值ne(θ')1，即

由公式10计算得到折射角θ'的第一次迭代值θ'1，即

第二次迭代：设折射角θ'的为θ'1，代入公式12，可以得到ψ的第二次迭代值ψ2，即

ψ2＝90°－θ'1－α

将ψ2代入公式13，得到ve(θ')的第二次迭代值值ve(θ')2，即

ve(θ′)2＝vo²cos²ψ2+ve²sin²ψ2

由公式11可以计算ne(θ')的第二次迭代值ne(θ')2，即

由公式10计算得到折射角θ'的第二次迭代值θ'2，即

第x次迭代：重复以上迭代方法，第x次迭代时，设折射角θ'的为θ'x-1，代入公式12，可以得到ψ的第x次迭代值ψx，即

ψx＝90°－θ'x-1－α

将ψx代入公式13，得到ve(θ')的第x次迭代值值ve(θ')x，即

ve(θ′)x＝vo²cos²ψx+ve²sin²ψx

由公式11可以计算ne(θ')的第x次迭代值ne(θ')x，即

由公式10计算得到折射角θ'的第x次迭代值θ'x，即

因为折射角θ'的真值本身就与入射角θ接近，所以本迭代算法中，第一次迭代将折射角θ'的初始值设为θ，如果第一迭代将折射角θ'的初始值设为其它值，经多次迭代仍然可以足够逼近θ'的真值，只不过所述初始值与θ'真值偏差较大时需要的迭代次数更多。

每一次迭代，θ'x的值都会更逼近θ'的真实值，比较θ'x和θ'x-1的差异，如果θ'x和θ'x-1的差异已经很小，表示当前迭代结果可以作为θ'的真值进行后续计算，具体迭代次数由样品2的具体特性和测试中对实验数据的精度要求决定。经实验验证，对于现有的用于制作大口径低吸收系数的的单轴晶体材料，当入射角为5°时，用本发明的方法经过4次迭代，即可保证θ'的迭代值小数点后6位保持不变。故本实施例取x＝4，即用θ'第四次迭代值作为θ'的真值，即

θ'＝θ'4公式14

联立公式4、公式7、公式9、公式14，得到样品2对e光的吸收系数并将其显示在计算机屏幕上。

测试结束后，关闭吸收系数测试程序，关闭光源1、探测器4、计算机5。