一种基于畸变拖曳阵的保真增强波束形成的方法与流程

本发明属于声纳信号处理领域，具体涉及一种基于畸变拖曳阵的保真增强波束形成的方法。

背景技术：

当前的声纳系统主要分为水听器岸基阵声纳和水听器拖曳线列阵声纳。水听器拖曳线列阵声纳简称拖曳阵，是拖曳在舰船尾部一定距离的声探测系统，通过接收航行目标自身的辐射噪声或反射的主动信号，来检测目标的有无并估计目标的有关参数。它具有探测能力强，探测频率低，水文适应能力强和无盲区的特点。水听器阵列流形是水听器阵列的一个重要参数，利用水听器阵列接收信号作波束形成等声纳信号处理时，一般都要求阵形己知。然而水听器阵列布放到水中之后，其阵形不好控制，一般认为当阵形畸变超过λ/10(λ为接收信号波长)时，就应在波束形成时对阵形畸变进行补偿，否则会对拖曳线列阵声呐性能产生重大影响，从而影响方位估计性能。

现有的拖曳阵阵形估计方法主要可以分为两类：一类是声学计算的方法，它是利用水听器阵列的接收信号来反推出阵列流形；另一类是非声辅助测量的方法，主要是在水听器拖曳阵上安装若干个深度或航向传感器，利用这些传感器的测量值来估计出阵形，实现畸变线列阵的保真波束形成。

声学计算的方法主要有锐度提取法和特征矢量法。锐度提取法在阵元较多的情况下搜索算法过于复杂，随后很少有人研究，之后该方法被应用于阵形未知的自适应波束形成，但是相比于该方法，特征矢量法性能较好。该方法只需要一个声源就可以估计出阵形。但一般要求声源方位精确已知，此外，它还要求首阵元的坐标已知，阵列形变不是很大，相邻阵元间距己知且固定。除了这两种方法外，还可以用最大似然估计方法和隐藏马尔科夫模型的方法估计畸变，实现畸变线列阵的较精确的波束形成。

非声辅助测量方法也主要有两种，流体力学法和插值拟合法。流体力学法将辅助传感器的测量值作为边界条件，通过求解拖缆的流体力学方程来估计畸变。这种方法为了得到更加精确的估计结果，往往在阵列尾部安装另一个航向传感器以做修正。另外，在方程中，阵列所受到的牵引力只来自阵列前端的拖点处。然而在实际情况中，当海况不好时，阵列会受到海浪涌流等因素的影响，这种方法估计出来的波束形成结果不太可信。插值拟合法是用辅助传感器测量阵列上的多点状态，然后用样条插值拟合出畸变的阵形实现精确的波束形成。这种方法假设各航向传感器的横坐标一直保持不变，即仍然等于阵列没有形变时的横坐标，因此估计出来的阵形与实际的阵形会有差别，阵列的总长度会拉长。当阵形变化较小时，这种差别影响不大，但当阵形变化较大时就需要对估计出的阵形做修正，从而使波束形成的结果更接近于真实值，提高阵列的方位估计性能。

自从1917年第一套拖曳阵声纳系统被发明以来，拖曳阵的发展已经经历了100年的时间。如今，拖曳阵在军事目标定向及海洋地层、石油勘探等商业领域都得到广泛地应用。其中，大多数应用都是基于阵列流形己知的前提，然而，由于海洋环境的复杂多变，水听器阵列在拖曳过程中，海浪、涌流、拖船机动都会改变阵列的形状，即阵列流形在拖曳过程中是不断变化的。常用的解决办法是假设拖曳阵始终保持为一条直线阵，但是在军事安全和商业利益的双重推动下，拖曳阵不断地向多基元、长距离、多维化的大规模方向发展，导致阵列在拖曳过程中阵形越来越难控制，这种假设阵形不变的做法不能满足实际应用需求。关于畸变的拖曳线列阵的目标方位估计准确度问题日显突出。如何在拖曳线列阵发生畸变的情况下，更为准确的进行目标信号的方位估计将成为提高阵列探测性能、促使拖曳阵走向高精度、高分辨率应用方向的关键。

目前已有多种针对畸变的拖曳线列阵进行估计的方法，一种最常用的途径是在拖线阵上放置多个水平深度测量仪，以获得阵元的位置信息，进而估计阵形，实现较精确的波束形成和目标信号方位估计。这种方法应用起来比较直接，但是经济代价太高。另外一种方法是通过估计误差参数来实现对阵形的校正，该类方法首先对阵列误差进行建模，将阵列误差校正转化为参数估计的问题。该类阵形校正方法通常可以分为有源校正类和自校正类。对于有源校正方法，该方法对辅助信号源有着较高的精确方位信息的要求，所以当辅助信号源的方位信息有偏差时，这类校正算法会带来较大的偏差。自校正算法由于阵元位置误差与方位参数之间的耦合和某些病态的阵列结构，参数估计的唯一辨识往往无法保证，更为重要的是参数联合估计对应的高维、多模非线性优化问题带来了庞大的运算量，估计的全局收敛性往往无法保证。

技术实现要素：

发明目的：针对现有技术中存在的问题，本发明公开了一种基于畸变拖曳阵的保真增强波束形成的方法，该方法通过时延估计来校正拖曳线列阵的畸变对波束形成影响，获得保真增强的目标辐射噪声跟踪波束。

技术方案：本发明采用如下技术方案：

一种基于畸变拖曳阵的保真增强波束形成的方法，包括如下步骤：

(1)模拟水声目标辐射噪声s(t)；

(2)模拟观测阵列信号xi(t)，i＝1,2,...,m，m为拖曳阵中阵元数目；

(3)基于理想波束形成粗略估计目标方位为目标信号波束能量最大时的引导角；

(4)检测目标信号的l个功率最大的线谱位置l＝1,2,...,l；

(5)由强线谱位置处的相位差估计拖曳阵中每个阵元的平均时延差δτi，i＝1,2,...,m；

(6)基于估计时延获取保真增强的目标跟踪波束

具体地，水声目标辐射噪声s(t)包括平稳连续谱分量sc(t)和线谱分量sl(t)；

所述平稳连续谱分量sc(t)的获取步骤如下：

(a.1)采用三参数模型法模拟平稳连续谱的功率谱gxf(ωt)：

其中ωm，ωc和λ为三参数模型的三个参数，决定了该连续谱的形状；ωt为频率，ωm为尖锐度因子，决定谱锋的尖锐程度和高度，ωc决定谱锋的位置，λ决定功率谱高、低频端幅度的相对比例，σ表示平稳连续谱信号的能量；

(a.2)建立p阶ar滤波器，其yule-walker方程为：

其中a[l]，l∈{1,2,…,p}和b0为p阶ar滤波器系数，δ[k]为冲击函数；rx[k]为gxf(ωt)的自相关函数rc(τ)的采样值；

(a.3)采用levison-durbin算法求解式(2)方程，得到p阶ar滤波器系数；高斯白噪声通过该ar滤波器后得到的信号，即为水声目标辐射噪声中的平稳连续谱分量sc(t)；

所述线谱分量sl(t)的获取步骤如下：

(b.1)采用k个正弦信号来模拟目标信号的线谱分量，其中ak为正弦信号幅度，fk为正弦信号的频率，t∈[0,t]为观测时间；

(b.2)在线谱位置fk处计算平稳连续谱分量sc(t)的能量pik，k＝1,2,...,k；

(b.3)根据已知的信号干扰比计算出各个正弦信号幅度ak，即得到水声目标辐射噪声中的线谱分量sl(t)。

具体地，步骤(2)包括如下步骤：

(2.1)将拖曳阵中第一个阵元设置为参考阵元，其阵元数据为：

s1(t)＝s(t)；

(2.2)拖曳阵中其余m-1个阵元的阵元数据为：

si(t)＝s[t-timedelay(i)]，i＝2,…,m；

其中timedelay(i)为第i个阵元相对于参考阵元的时延：

tardis(i)为声源与第i个阵元之间的距离，v是声音在水中的传播速度。

(2.3)根据已知的信噪比计算能量pn，并生成能量为pn的m路高斯白噪声ni(t)，其中i＝1,…,m，sl(t)为水声目标辐射噪声线谱分量；

(2.4)观测阵列信号xi(t)为：xi(t)＝si(t)+ni(t)。

具体地，步骤(3)包括如下步骤：

(3.1)计算理想均匀线阵在引导角θm下相邻阵元时延τm：

其中m＝1,…,m+1，m+1为总引导角个数，d为相邻阵元间的距离；

(3.2)对各阵元数据进行延时相加，得到目标信号波束能量图：

(3.3)通过能量检测找到波束能量最大值位置时的引导角为目标方位的粗估计

具体地，步骤(4)包括如下步骤：

(4.1)根据粗估计的目标方位计算各阵元的时延估计

(4.2)将各阵元数据按时延估计与参考阵元对齐，对对齐后的阵元数据相干相加获得目标跟踪波束g(t)：

(4.3)对g(t)进行傅里叶变换获得目标信号频谱g(ω)，同时利用滑动窗平滑技术估计目标信号连续谱gc(ω)，在目标信号频谱g(ω)中删除连续谱gc(ω)的影响，获得目标信号的线谱gl(ω)，利用能量检测估计出l个功率最大的线谱l＝1,…,l，其中l为估计线谱的数目；

(4.4)计算拖曳阵中每个阵元的频点其中i＝1,…,m，l＝1,…,l；则第i个阵元、第l个线谱的相位为其中phase[·]为计算信号相位运算。

具体地，步骤(5)包括如下步骤：

对于l个强线谱获得第i个阵元平均时延差为其中δτil为第l个线谱位置处第i个和第i-1个阵元相位差，和分别为第l个线谱位置处第i个和第i-1个阵元的相位。

具体地，步骤(6)包括如下步骤：

(6.1)计算第i个阵元与参考阵元的时延差ζi：其中δτ0为第j个阵元平均时延差；

(6.2)获得保真增强的目标跟踪波束

有益效果：本发明公开的基于畸变拖曳阵的保真增强波束形成的方法，首先使用基于理想阵形的波束形成方法对目标信号的来波方向进行粗估计；然后利用来波方向获得目标信号的跟踪波束，其次对跟踪波束进行傅里叶变换获得目标频谱特性，同时在频率域进行目标强线谱检测；基于检测的线谱信息，对各阵元数据利用傅里叶变换计算对应线谱；最后，提取各个阵元的线谱相位，通过计算相邻阵元相位差估计出相邻阵元的时延，同时利用估计的时延对各阵元信号进行延时对齐，从而实现在畸变阵形环境下的保真增强的波束形成。与现有技术相比，本发明公开的方法具有以下优点：本发明公开的波束形成方法直接从接收到的阵元数据估计线谱，基于估计线谱相位估计相邻阵元间的时延，实现了自适应的基于畸变拖曳阵的保真增强波束形成技术，应用简单直接，经济代价低且效果明显，运算量较小，校正精度较高。

附图说明

图1为本发明方法的流程图；

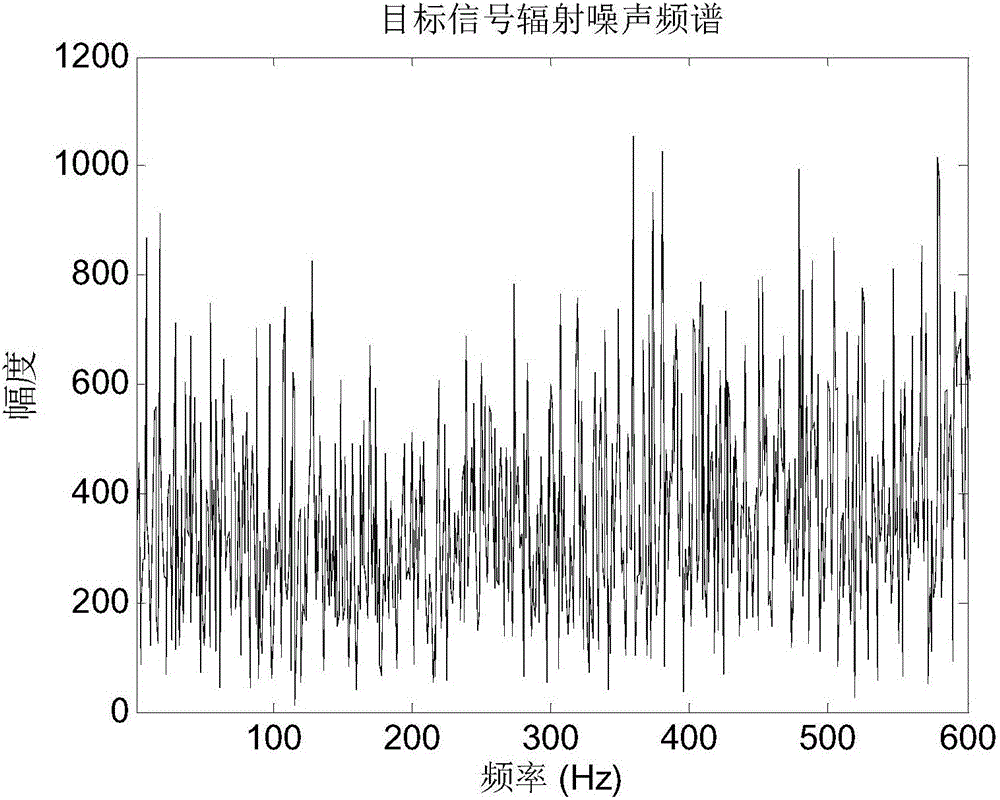
图2为实施例1中目标辐射噪声信号的频谱；

图3为实施例1中畸变拖曳阵的阵元位置图；

图4为实施例1中基于理想阵形的波束能量图；

图5为实施例1中真实时延、基于理想阵的估计时延与校正后时延的对比图；

图6为实施例1中原始数据频谱、基于理想位置的跟踪波束频谱以及校正后的跟踪波束频谱的对比图；

图7为实施例2中跟踪波束线谱幅度误差随信噪比变化示意图。

具体实施方式

下面结合附图和具体实施方式，进一步阐明本发明。

一种基于畸变拖曳阵的保真增强波束形成的方法，如图1所示，包括如下步骤：

步骤1、模拟水声目标辐射噪声s(t)；

水声目标辐射噪声s(t)包括平稳连续谱分量sc(t)和线谱分量sl(t)，即：

s(t)＝sc(t)+sl(t)

所述平稳连续谱分量sc(t)的获取步骤如下：

(a.1)采用经典的三参数模型法模拟平稳连续谱的功率谱gxf(ωt)：

其中ωm，ωc和λ为三参数模型的三个参数，决定了该连续谱的形状；ωt为频率，ωm为尖锐度因子，决定谱锋的尖锐程度和高度，ωc决定谱锋的位置，λ决定功率谱高、低频端幅度的相对比例，σ表示平稳连续谱信号的能量；

(a.2)根据wiener-khinchin定理，式(1)的逆傅里叶变换即为平稳连续谱信号的自相关函数rc(τ)，可写成：

rc(τ)＝σexp(-ωm|τ|)[cosωcτ+λsin(ωc|τ|)]

假设以fs为采样率对时域信号进行等间隔采样，则上述自相关函数可以写成离散形式为，

rc(kts)＝σexp(-ωm|kts|)[cosωckts+λsin(ωc|kts|)]

其中ts＝1/fs；根据式(1)建立p阶ar滤波器，其yule-walker方程为：

其中a[l]，l∈{1,2,…,p}和b0为p阶ar滤波器系数，δ[k]为冲击函数；rx[k]为gxf(ωt)的自相关函数rc(τ)的采样值；

(a.3)采用levison-durbin算法求解式(2)方程，得到p阶ar滤波器系数；高斯白噪声通过该ar滤波器后得到的信号，即为水声目标辐射噪声中的平稳连续谱分量sc(t)；

所述线谱分量sl(t)的获取步骤如下：

(b.1)采用k个正弦信号来模拟目标信号的线谱分量，其中ak为正弦信号幅度，fk为正弦信号的频率，t∈[0,t]为观测时间；

(b.2)在线谱位置fk处计算平稳连续谱分量sc(t)的能量pik，k＝1,2,...,k；

(b.3)根据已知的信号干扰比计算出各个正弦信号幅度ak，即得到水声目标辐射噪声中的线谱分量sl(t)。

步骤2、模拟观测阵列信号xi(t)；假设拖曳阵为有m个阵元的畸变阵形，即i＝1,2,...,m；通过步骤(2.1)至(2.4)得到观测阵列信号：

(2.1)将拖曳阵中第一个阵元设置为参考阵元，其阵元数据为：

s1(t)＝s(t)；

(2.2)拖曳阵中其余m-1个阵元的阵元数据为：

si(t)＝s[t-timedelay(i)]，i＝2,…,m；

其中timedelay(i)为第i个阵元相对于参考阵元的时延：

tardis(i)为声源即目标与第i个阵元之间的距离，v是声音在水中的传播速度；

(2.3)根据已知的信噪比计算能量pn，并生成能量为pn的m路高斯白噪声ni(t)，其中i＝1,…,m，sl(t)为水声目标辐射噪声线谱分量；

(2.4)观测阵列信号xi(t)为：xi(t)＝si(t)+ni(t)；

步骤3、基于理想波束形成粗略估计目标方位为目标信号波束能量最大时的引导角；具体包括如下步骤：

(3.1)由于无法事先获知阵形的畸变状况，首先进行基于理想阵形，即均匀线阵的波束形成；第i个阵元到参考阵元之间的时间差为τi＝(i-1)τ，其中τ为相邻阵元时延差。考虑到拖曳水听器的柔性结构，假设相邻阵元间距d保持不变；在引导角θm下相邻阵元时延τm：

其中m＝1,…,m+1，m+1为总引导角个数，d为相邻阵元间的距离；

(3.2)对各阵元数据进行延时相加，得到目标信号波束能量图：

(3.3)通过能量检测找到波束能量最大值位置时的引导角为目标方位的粗估计

步骤4、检测目标信号的l个功率最大的线谱位置l＝1,2,...,l；具体包括如下步骤：

(4.1)根据粗估计的目标方位计算各阵元的时延估计

(4.2)将各阵元数据按时延估计与参考阵元对齐，对对齐后的阵元数据相干相加获得目标跟踪波束g(t)：

(4.3)对g(t)进行傅里叶变换获得目标信号频谱g(ω)，同时利用滑动窗平滑技术估计目标信号连续谱gc(ω)，在目标信号频谱g(ω)中删除连续谱gc(ω)的影响，获得目标信号的线谱gl(ω)，利用能量检测估计出l个功率最大的线谱l＝1,…,l，其中l为估计线谱的数目；

(4.4)计算拖曳阵中每个阵元的频点其中i＝1,…,m，l＝1,…,l；则第i个阵元、第l个线谱的相位为其中phase[·]为计算信号相位运算。

步骤5、由强线谱位置处的相位差估计拖曳阵中每个阵元的平均时延差δτi，i＝1,2,...,m；具体步骤为：

对于l个强线谱获得第i个阵元平均时延差为其中δτil为第l个线谱位置处第i个和第i-1个阵元相位差，和分别为第l个线谱位置处第i个和第i-1个阵元的相位。

步骤6、基于估计时延获取保真增强的目标跟踪波束具体包括：

(6.1)计算第i个阵元与参考阵元的时延差ζi：其中δτj为第j个阵元平均时延差；

(6.2)获得保真增强的目标跟踪波束

实施例1：

本实施例中，采样频率fs＝32khz，声音在水中的传播速度v取为1500m/s。利用三参数模型法模拟水声目标辐射噪声的平稳连续谱的功率谱gxf，仿真过程中三参数设置如下：ωm＝2π×500rad/s，ωc＝2π×1000rad/s，λ＝0，平稳连续谱信号能量σ＝1。

模拟目标辐射噪声的6个线谱分量：通过线谱位置处平稳连续谱的能量pi和已知的信号干扰比sir＝10，由获得各个正弦信号的幅度ai。正弦信号的频率fi分别为20hz，45hz，60hz，100hz，200hz，500hz。观测时间为t＝20s。将平稳连续谱分量以及线谱分量加起来，获得目标辐射噪声信号s(t)。目标辐射噪声信号的频谱如图2所示。

本实施例中，拖曳阵数目m＝100，阵元间距d＝0.8，畸变阵列的各阵元具体位置如图3所示。假设目标与阵元法线方向的夹角为30°，与参考阵元的距离为1000m。设声源与第i个阵元之间的距离差为tardis(i)，则第i个阵元相对于参考阵元的时延timedelay(i)可以写成：

将图2所示的信号作为参考阵元的阵元数据，对于第i个阵元，依照时延公式对参考阵元信号进行时延，由此获得100个阵元的阵列数据。对各阵元数据si(t)添加高斯白噪声，信噪比为-15db，获得观测数据xi(t)。

在此实施例中，基于理想阵形的波束形成如图4所示。通过能量检测找到波束能量最大值位置得到目标方位的粗估计

图5给出了畸变拖曳阵相邻阵元间的真实时延、基于理想线阵估计出的相邻阵元时延以及根据强线谱得到的相位差估计出的相邻阵元时延。其中曲线1为基于理想阵形的估计时延，曲线2为理论时延，曲线3为根据强线谱得到的相位差估计出的相邻阵元时延。从图中可以看出，本发明公开的方法能够有效地估计出畸变拖曳线列阵阵元间的时延。

图6给出了原始数据频谱，基于理想位置的跟踪波束频谱以及校正后的跟踪目标频谱的对比图。从图中可以看出，与传统的波束形成方法相比，本发明公开的保真增强波束形成方法形成的波束频谱更加接近于原始数据真实值，波束形成的效果得到了保真增强。

实施例2：

本实施例主要分析和验证信噪比对本发明公开的保真增强波束形成的影响。观测时间为t＝20s。数据信噪比从-45db到-10db，对于每个信噪比，设估计波束形成的幅度相对误差为e，ai表示原始数据频谱在第i个线谱位置处的幅度，pai表示估计波束形成频谱在第i个线谱位置处的幅度。以跟踪波束线谱幅度相对误差作为性能评价指标。如图7给出了线谱重建误差随信噪比变化示意图。从图中可以看出，随着信噪比提高，基于保真增强波束形成的重建误差逐渐较小；而基于理想阵形的波束形成方法由于其没有有效的阵形校正能力，随着信噪比的提高，其重建误差随信噪比变化很小。