一种基于相关向量机和粒子滤波的动力电池系统剩余可用寿命预测方法与流程

本发明涉及动力电池的预测与健康状态管理领域，尤其涉及基于少量老化数据建立动力电池的老化模型，以及基于该模型对可用寿命进行预测。

背景技术：

动力电池系统的剩余可用寿命(remainingusefullife:rul)用于指示其在健康状态条件下的剩余寿命时间。动力电池的rul预测能够帮助生产企业精确评估产品的寿命时间，进而制定出具有经济性、竞争力的产品质保期，同时可以帮助用户提前维修保养、更换电池系统，避免不必要的损失。早期的剩余寿命预测算法基于相关向量机(relevancevectormachine:rvm)从电化学阻抗谱(electrochemicalimpedancespectroscopy:eis)测试数据中提取电池特征值构建动力电池老化模型，并基于粒子滤波(particlefilter:pf)理论更新模型参数、预测电池rul。因为eis只能离线测量，因此该方法只能用于离线预测动力电池的rul。为了克服这种限制，又出现了可基于d-s证据理论(dempster-shafertheory:dst)以及贝叶斯蒙特卡罗方法(bayesianmontecarlo:bmc)构建的方法论进行在线预测。这种方法论首先利用dst基于多组离线数据初始化动力电池老化模型，然后利用bmc基于动力电池容量在线监测数据更新模型参数、预测动力电池rul。基于这一理论体系，后续又有系列研究成果实现了动力电池老化模型的精度以及滤波性能的提升，从而更精确的预测了动力电池的rul。然而该理论体系需要依据一支或多支动力电池实验数据初始化动力电池老化模型。该初始化过程需要大量的离线训练数据来构建精确的老化模型。此外，如果实际工作中的电池与实验电池的工作环境不同，会得出错误的初始化模型。并且，电池生产过程中的特性不一致会进一步增大模型初始化误差。为了解决这些问题，有研究提出了基于rvm以及三参数容量衰退模型的理论体系预测动力电池rul。其中，rvm基于动力电池运行过程中的历史数据提取特征向量，然后使用这些提取的特征向量拟合三参数容量衰退模型。该方法减少了训练数据，并降低了由于电池工作条件以及特性不一致性引发的建模误差。然而，三参数容量衰退模型指数函数项的指数是经验性的通过观测容量衰减速率获取，如果指数选取不准确，rul预测值可能会远远偏离真实值。

因此，在当前应用背景技术下，如何基于少量、有限的老化数据实现动力电池老化模型的精确构建并进行rul的在线精确、可靠预测具有重要的理论价值和应用意义。

技术实现要素：

针对上述本领域中存在的技术问题，本发明提供了一种基于相关向量机和粒子滤波的动力电池系统剩余可用寿命预测方法，具体包括以下步骤：

步骤一，在线获取动力电池系统的容量衰退数据；

步骤二，利用相关向量机提取所述容量衰退数据的特征向量；

步骤三，利用非线性最小二乘回归方法拟合动力电池老化模型；

步骤四，构建描述动力电池老化的状态空间方程；

步骤五，基于粒子滤波理论预测动力电池系统的剩余可用寿命。

进一步地，所述步骤一具体包括：在线获取动力电池容量测量值y＝(y1,y2,…,yn)^t以及对应的充放电循环次数k＝(1,2,…,n)^t。其中，y1,y2,…,yn代表循环次数1,2,…,n时的动力电池容量测量值。

进一步地，所述步骤二具体包括：将步骤一中在线获取的数据用于模型训练，将充放电循环次数k＝(1,2,…,n)^t作为输入，容量测量值y＝(y1,y2,…,yn)^t为输出，得到训练好的相关向量机，同时得到相关向量其中l＝(l1,l2,…,lm)^t为构成相关向量的动力电池充放电循环次数，为构成相关向量的对应充放电循环次数条件下的容量测量值。

进一步地，所述步骤三具体包括：建立动力电池系统的老化模型为：y＝a·exp(b·l)+c·l^d，其中模型输出值y为动力电池容量，模型参数l为动力电池充放电循环次数，模型参数a和b与电池内阻有关，c和d代表电池老化速率。d的值预设为2。使用非线性最小二乘回归方法对该模型进行拟合，拟合数据为步骤二获得的相关向量从而拟合得到模型的其他三个参数值a，b以及c。

进一步地，所述步骤四中的状态空间方程为：

其中，k为动力电池充放电循环次数，χk和yk分别为动力电池系统在k次充放电循环时的状态矩阵和观测矩阵，ωk和vk分别为k次充放电循环时的过程噪声矩阵以及测量噪声矩阵，ak、bk、ck、dk为模型参数a、b、c、d在k次充放电循环时的值，其中，a0、b0、c0、d0为步骤三所获得的拟合值以及预设值。

进一步地，所述步骤五中基于粒子滤波理论预测动力电池系统的剩余可用寿命具体包括：

5.1).初始化:

其中，为系统第i个粒子0次循环时的状态矩阵预设值，为系统第i个粒子0次循环时的过程噪声矩阵，为系统第i个粒子1次循环时的状态矩阵估计值，np为所产生的粒子数，为系统第i个粒子1次循环时的权系数。

5.2).对于k∈{2,…,∞}，实施计算，计算流程如下：

5.2.1).更新粒子权系数wk：

(1)产生随机变量：

其中，为系统第i个粒子k次循环时的状态矩阵，χk为系统k次循环时的状态矩阵估计值，yk为系统k次循环时的容量观测值，q(●)为用户定义的概率密度函数，此处定义为基于状态方程统计特性的概率分布密度函数；

(2)计算非归一化的粒子权系数值：

其中，为系统第i个粒子k次循环时的非归一化权系数值，为第i个粒子k-1次循环时的归一化权系数值，f(●)为基于状态空间方程统计特性的概率密度分布函数；

(3)归一化粒子权系数：

5.2.2).重采样。

评估有效粒子数以判断是否需要进行重采样：

如果neff<nmin，粒子进行重采样。其中neff为计算获得的有效粒子数，nmin为用户定义的有效粒子数的最小值。

5.2.3).计算系统状态矩阵估计值χk。

对np个粒子加权获得χk：

5.2.4).预测动力电池系统剩余可用寿命及概率分布函数，计算流程如下：

(1)将系统状态估计值带入观测方程预测多个粒子动力电池系统的容量衰退：

其中，为系统第i个粒子l⁽ⁱ⁾次循环时的容量预测值，如果(q为初始容量)，则l⁽ⁱ⁾即为动力电池系统总的可用寿命循环次数。

(2)计算多个粒子动力电池系统剩余可用寿命预测值：

rul⁽ⁱ⁾＝l⁽ⁱ⁾-k

其中，k为预测起始循环次数，rul⁽ⁱ⁾为第i个粒子的剩余可用寿命循环次数。

(3)对np个粒子加权获得动力电池容量、剩余寿命预测值：

其中，l为预测的系统循环次数，为系统第i个粒子l次循环时的容量预测值，为系统l次循环时的容量预测值，为系统剩余可用寿命。

(4)获得动力电池剩余寿命概率分布密度函数：

其中，y1:k为第一个循环至k个循环的容量观测值，δ(·)为狄拉克函数。

至此，完成了动力电池系统的剩余可用寿命的预测。

本发明所提供的方法具有可有效降低训练数据量、提高算法的预测精度、保证rul估计器的稳定性等诸多有益效果，有望在实际应用中获得精确、可靠的预测结果。

附图说明

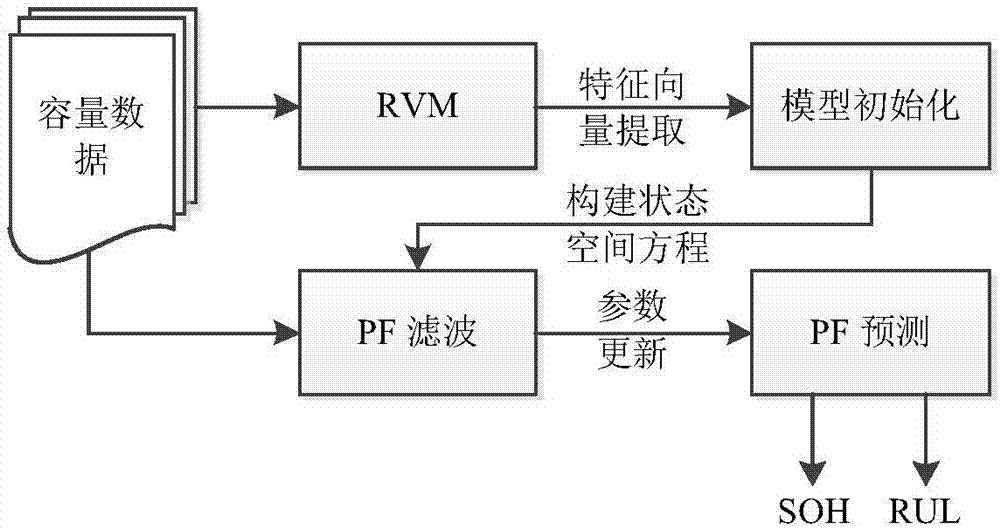
图1为动力电池soh估计与rul预测流程图

图2为动力电池系统容量衰减实验数据

图3为基于30％训练数据的动力电池系统老化模型初始化及rul预测结果

图4为基于75％训练数据的动力电池系统老化模型初始化及rul预测结果

具体实施方式

下面结合图1进一步解释本发明所提供的方法，其具体包括以下步骤：

步骤一，在线获取动力电池系统的容量衰退数据；

步骤二，利用相关向量机提取所述容量衰退数据的特征向量；

步骤三，利用非线性最小二乘回归方法拟合动力电池老化模型；

步骤四，构建描述动力电池老化的状态空间方程；

步骤五，基于粒子滤波理论预测动力电池系统的剩余可用寿命。

在本申请的一个优选实施例中，所述步骤一具体包括：在线获取动力电池容量测量值y＝(y1,y2,…,yn)^t以及对应的充放电循环次数k＝(1,2,…,n)^t。其中，y1,y2,…,yn代表充放电循环次数为1,2,…,n时的动力电池容量测量值。

在本申请的一个优选实施例中，所述步骤二具体包括：将步骤一中在线获取的数据用于模型训练，将充放电循环次数k＝(1,2,…,n)^t作为输入，容量测量值y＝(y1,y2,…,yn)^t为输出，得到训练好的相关向量机，同时得到相关向量其中l＝(l1,l2,…,lm)^t为构成相关向量的动力电池充放电循环次数，为构成相关向量的对应充放电循环次数条件下的容量测量值。

在本申请的一个优选实施例中，所述步骤三具体包括：建立动力电池系统的老化模型为：y＝a·exp(b·l)+c·l^d，其中模型输出值y为动力电池容量，模型参数l为动力电池充放电循环次数，模型参数a和b与电池内阻有关，c和d代表电池老化速率。d的值预设为2。使用非线性最小二乘回归方法对该模型进行拟合，拟合数据为步骤二获得的相关向量从而拟合得到模型的其他三个参数值a，b以及c。

在本申请的一个优选实施例中，所述步骤四中的状态空间方程为：

其中，k为动力电池充放电循环次数，χk和yk分别为动力电池系统在k次充放电循环时的状态矩阵和观测矩阵，ωk和vk分别为k次充放电循环时的过程噪声矩阵以及测量噪声矩阵，ak、bk、ck、dk为模型参数a、b、c、d在k次充放电循环时的值，其中，a0、b0、c0、d0为步骤三所获得的拟合值以及预设值。

在本申请的一个优选实施例中，所述步骤五中基于粒子滤波理论预测动力电池系统的剩余可用寿命具体包括：

5.1).初始化:

其中，为系统第i个粒子0次循环时的状态矩阵预设值，为系统第i个粒子0次循环时的过程噪声矩阵，为系统第i个粒子1次循环时的状态矩阵估计值，np为所产生的粒子数，为系统第i个粒子1次循环时的权系数。

5.2).对于k∈{2,…,∞}，实施计算，计算流程如下：

5.2.1).更新粒子权系数wk：

(1)产生随机变量：

其中，为系统第i个粒子k次循环时的状态矩阵，χk为系统k次循环时的状态矩阵估计值，yk为系统k次循环时的容量观测值，q(●)为用户定义的概率密度函数，此处定义为基于状态方程统计特性的概率分布密度函数；

(2)计算非归一化的粒子权系数值：

其中，为系统第i个粒子k次循环时的非归一化权系数值，为第i个粒子k-1次循环时的归一化权系数值，f(●)为基于状态空间方程统计特性的概率密度分布函数；

(3)归一化粒子权系数：

5.2.2).重采样。

评估有效粒子数以判断是否需要进行重采样：

如果neff<nmin，粒子进行重采样。其中neff为计算获得的有效粒子数，nmin为用户定义的有效粒子数的最小值。

5.2.3).计算系统状态矩阵估计值χk。

对np个粒子加权获得χk：

5.2.4).预测动力电池系统剩余可用寿命及概率分布函数，计算流程如下：

(1)将系统状态估计值带入观测方程预测多个粒子动力电池系统的容量衰退：

其中，为系统第i个粒子l⁽ⁱ⁾次循环时的容量预测值，如果(q为初始容量)，则l⁽ⁱ⁾即为动力电池系统总的可用寿命循环次数。

(2)计算多个粒子动力电池系统剩余可用寿命预测值：

rul⁽ⁱ⁾＝l⁽ⁱ⁾-k

其中，k为预测起始循环次数，rul⁽ⁱ⁾为第i个粒子的剩余可用寿命循环次数。

(3)对np个粒子加权获得动力电池容量、剩余寿命预测值：

其中，l为预测的系统循环次数，为系统第i个粒子l次循环时的容量预测值，为系统l次循环时的容量预测值，为系统剩余可用寿命。

(4)获得动力电池剩余寿命概率分布密度函数：

其中，y1:k为第一个循环至k个循环的容量观测值，δ(·)为狄拉克函数。

图2示出了动力电池系统的容量衰减实验数据，该数据前一部分将用于初始化动力电池系统老化模型，后一部分数据将用于验证动力电池系统rul预测的精度。动力电池系统在第800个循环容量衰减至初始容量的80％。400个循环之前的容量数据衰减率出现递减趋势，400个循环以后容量呈直线衰减，与之前相比衰减加速。前后不同的衰减趋势进一步加大了动力电池系统rul精确预测的难度。

图3示出了动力电池系统老化模型初始化(图3(a))以及rul预测(图3(b))结果，此时在线获得的容量数据为整个容量衰减数据量的30％。图3(a)中的拟合值代表初始化模型的容量衰减与循环次数的关系，相关向量为rvm训练结束后自动产生。虽然只有30％的数据用于训练，但是初始化的模型能够很好地预测动力电池容量的衰减趋势，此时预测的系统失效循环次数为684，即rul预测误差为116次。图3(b)中的预测值为基于pf的系统容量预测结果，前30％的数据仍然用于状态空间方程参数的更新，rulpdf为rul预测值的概率分布函数(probabilitydistributionfunction:pdf)。此时，动力电池系统失效循环次数预测值为782次，rul预测误差仅为18次，失效循环次数pdf的95％范围分布为：720-850。可见，进一步更新参数后的模型精度有了明显提升。该仿真结果意味着生产企业在进行动力电池系统加速寿命实验时，仅需花费整个加速寿命30％的时间便可对系统寿命进行精确评估，从而大大降低了实验所需的人力和物力。

图4示出了动力电池系统老化模型初始化(图4(a))以及rul预测(图4(b))结果，此时在线获得的容量数据为整个容量衰减数据量的75％。当更多的容量数据用于训练rvm、提取动力电池系统容量衰减的特征向量时，初始化的模型对于400个循环以后的容量预测精度明显好于图3(a)，此时预测的失效循环次数为824，比真实值800多了24个循环。因此，当pf基于该初始化的老化模型进行rul预测时，精度会有明显提升(图4(b))，此时的预测失效循环次数为799，仅比真实值少了1个循环，动力电池系统失效循环次数预测pdf的95％范围为：755-840。该仿真结果表明，实际使用中，当动力电池管理系统在线采集到更多的容量衰减数据时，算法的预测精度将会大大提升。

尽管已经示出和描述了本发明的实施例，对于本领域的普通技术人员而言，可以理解在不脱离本发明的原理和精神的情况下可以对这些实施例进行多种变化、修改、替换和变型，本发明的范围由所附权利要求及其等同物限定。