一种地下构造的反演方法与流程

本发明涉及一种地下构造的反演方法，属于油气物探工程领域。

背景技术：

在碳酸盐岩储层中，孔、缝、洞构造是油气富集的重要场所，勘探的重点问题是如何实现孔、缝、洞等非均质构造的识别与成像。非均质构造的地震响应主要表现为绕射波场。

但是，绕射波相对于反射波能量较弱，在成像时绕射波对应的非均质构造通常会淹没在背景构造中，难以识别。此外，由于绕射波场能量太弱，在单独提取绕射波进行成像时，常规成像方法的结果更易受到噪音干扰，同时存在绕射波不收敛、成像分辨率低等问题。

基于此，我们需要更准确的地下构造反演方法。

技术实现要素：

本申请实施例提供一种地下构造的反演方法，用于解决以下问题中的至少一个：反演地下构造时，非均质构造难以识别的问题，或，反演地下构造时，非均质构造成像不准确的问题。

基于此，本申请实施例提供一种地下构造的反演方法，所述方法包括：

根据观测数据计算第一数据残差，获取第一数据残差中的绕射波场和反射波场；

根据预设的反射波场加权函数和所述反射波场、绕射波场，确定第二数据残差；

根据所述第二数据残差，进行迭代反演成像。

相较于现有技术而言，本申请实施例通过分离第一数据残差中的绕射波场和反射波场，并利用加权函数，对反射波场进行加权，以生成第二数据残差(也就是加权反射波场后的数据残差)进行迭代反演成像。本发明方法可以实现对地下孔缝洞等非均质地质结构的高精度成像；还可以通过改变加权函数，在迭代过程中不断降低反射波的权重，提高对地下孔缝洞等非均质结构的识别度。

附图说明

图1为本申请实施例提供的一个实施例的流程框图；

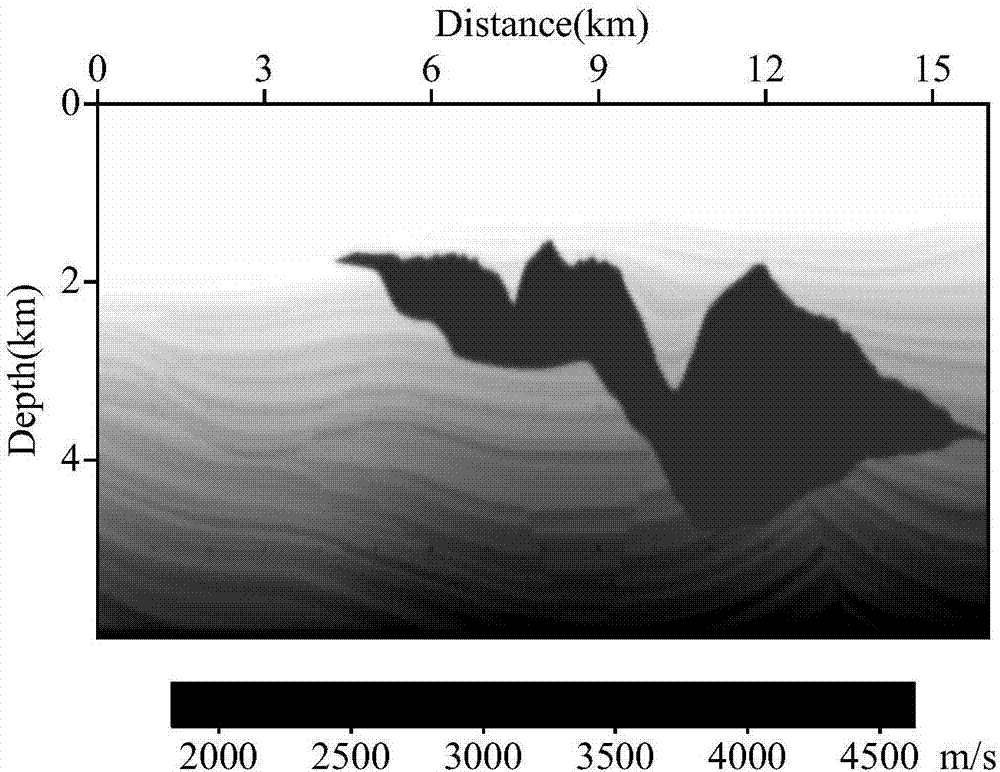
图2为本发明的一个实施例的偏移速度场；

图3为常规最小二乘逆时偏移成像结果；

图4为常规绕射波逆时偏移成像结果；

图5为本发明的一个实施例的绕射波最小二乘偏移成像结果；

图6为本发明的一个实施例的全波场最小二乘逆时偏移成像结果；

图7为本发明的实施例与其他两种方法结果的波数谱对比；

图8为本发明的实施例与常规最小二乘逆时偏移方法结果的归一化数据残差收敛曲线；

下面结合附图和具体实施方式对本发明作进一步的说明。

具体实施方式

为使本申请的目的、技术方案和优点更加清楚，下面将结合本申请具体实施例及相应的附图对本申请技术方案进行清楚、完整地描述。显然，所描述的实施例仅是本申请一部分实施例，而不是全部的实施例。基于本申请中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本申请保护的范围。

本申请实施例提供一种地下构造的反演方法，如图1所示，包括以下步骤：

s101，根据观测数据计算第一数据残差，获取第一数据残差中的绕射波场和反射波场。具体的说，包括如下步骤：

步骤a，获取模型数据与观测数据的差值，其中，所述模型数据是根据观测数据的成像结果和迭代次数所确定的；

即设置初始的成像结果为0(观测数据的成像结果需要不停迭代)，对当前的成像结果进行逆时反偏移，获得模型数据。

具体地说，通过逆时反偏移计算模型数据通过求解以下波动方程实现：

其中，v0(x)为偏移速度场，p(x,t)为逆时反偏移计算得到的模型数据，▽²为拉普拉斯算子，m(x)为成像结果，p0(x,t)为背景波场。求解背景波场的波动方程为：

其中，f(t)为震源子波。

获取模型数据与观测数据的差值，计算过程以矩阵运算的形式表示为：

r^(k)＝lm^(k-1)-d(3)

其中，r^(k)为在第k迭代时所对应的差值，也就是第一数据残差。

l为逆时反偏移算子，m^(k-1)为第k-1迭代时得到的成像结果，也就是对当前的成像结果进行逆时反偏移，获得模型数据p(x,t)，逆时反偏移通过求解式(1)所示的波动方程进行，d为观测数据，。

由于在反演过程中采用迭代的方式进行，每次迭代都会改变当前的成像结果，从而所述的模型数据和及第一数据残差也需要对应进行迭代。

步骤b，分离出所述差值中所包含的绕射波场。

在得到所述的差值之后，将所述差值由共炮点道集变换为共偏移距道集，对其进行常规的基于平面波解构滤波器的绕射波分离，得到绕射波场：

d^(k)＝sr^(k)(4)

其中，d^(k)为第k次迭代时差值中所包含的绕射波场，s为进行绕射波分离的平面波解构滤波器。

由于在共偏移距道集中，反射波对应于较为连续光滑的拟线性同相轴，绕射波对应于不连续、不平滑的双曲同相轴。通过用平面波解构滤波器可以估算出同相轴的局部倾角，去除连续光滑的反射波场，得到绕射波场。

步骤c，根据所述差值和绕射波场确定反射波场。

通过以下公式确定：

r^(k)＝r^(k)-d^(k)(5)

其中，r^(k)为第k次迭代时所述差值中的反射波场。

s102，根据预设的反射波场加权函数和所述反射波场、绕射波场，确定数据残差。具体的说，可通过以下方式确定所述数据残差：

其中，为第二数据残差，d^(k)为绕射波场，为反射波场加权函数，r^(k)为反射波场，k为迭代次数；其中，所述反射波场加权函数等于0，或，所述反射波场加权函数大于0且小于1。

若成像目标为地下的孔、缝、洞、断层等非均质地质体，则设置为0，则此时仅对绕射波场成像。以便后续通过迭代更新算法改善绕射波场的成像质量，提供地下非均质地质体的精确图像。

若成像目标为所有地下构造，则设置所述反射波场加权函数大于0且小于1，并且随迭代次数的增加而逐渐减小。此时的加权函数有多种构造形式，可根据成像目标人为给定。例如，设置为反射波场加权函数，b为控制反射波场加权系数大小的参数，b>0，以便后续迭代反演过程中突出绕射波场在目标函数中占的比重，进而改善绕射波场对应的非均质地质体的成像识别度。

s103，根据所述第二数据残差，进行迭代反演成像。

此时根据所述第二数据残差，确定目标函数和更新方向，对目标函数进行迭代反演即可。

可通过构建如下目标函数：进行迭代反演。其中j(m)为目标函数，m为成像结果，d为绕射波场，r和wr分别为反射波场及其反射波场加权函数，tλ为进行l1模约束的阈值函数，用以压制成像结果中小于阈值的信号。

确定更新方向的公式为：

其中，j(m)为目标函数，d^*(x,t)和r^*(x,t)为数据残差中绕射波场d(xg,t)和反射波场r(xg,t)的伴随波场，p0(x,t)为背景波场，x为地下任意一点，xg为接收点。绕射波场的伴随波场可通过以下波动方程计算：

同理，反射波场的伴随波场可通过以下波动方程计算：

然后判断更新方向是否满足误差条件，误差条件为：更新方向的2范数小于ε，ε是一个接近于0的正实数，可根据经验进行设定。若不满足误差条件则继续迭代，满足误差条件时迭代终止。

当更新方向的2范数大于ε，即误差条件不满足时，根据更新方向对成像结果进行迭代更新。具体地说，对成像结果进行迭代更新的公式为：

其中，m^(k)为第k迭代计算得到的成像结果，m^(k-1)为第k-1迭代计算得到的成像结果，为第k次迭代时的更新步长，g^(k)为第k次迭代时的更新方向，更新方向通过公式(7)求解。第k次迭代时进行l1模约束的阈值函数，可根据观测数据的信噪比人为给定，观测数据的信噪比越高，阈值越小。l1模约束通过阈值收缩法实现，在迭代次数较小时，选择较大的阈值快速地压制成像结果中的偏移噪音，随着迭代次数的增加，阈值逐渐减小，以更新目标信号对应的地质构造。

当更新方向的2范数小于ε时，判定当前的成像结果为最终成像结果，输出最终成像结果。

采用本发明的方法，通过设置不同的加权函数对反射波进行加权，以确定第二数据残差，在根据第二数据残差对绕射波成像时(也就是只对孔缝洞等非均质结构成像时)，本发明方法可以通过迭代更新算法改善绕射波场的成像质量，提供地下非均质地质体的精确图像；在根据第二数据残差对全波场成像时(也就是对全部地下结构成像时)，本发明方法在反射波场加权函数逐渐减小的过程中，首先更新反射波场对应的大尺度均质构造，改善其成像质量的同时逐渐减小反射波场在目标函数中的比重，突出绕射波场，提高了绕射波场对应的非均质结构的识别度，最终可以得到地下所有构造的高精度图像。

为使本发明的技术方案更加的浅显明白，下边给出一个具体应用的例子加以说明：

将本发明的方法应用在sigsbee2a模型为例，输入观测数据，包括偏移速度场(如图2所示)、观测地震数据、观测系统、反射波场的加权函数，l1模约束阈值函数，并设置初始的成像结果为0，观测系统分布为：在海面以100米间隔均匀布置160个炮点，由1600个在海底均匀布置的检波点接收，检波点间隔为10米，偏移参数如下：偏移速度场横向采样点为1600及纵向采样点为600，空间采样间隔为10米，时间采样间隔为0.6毫秒，采样时间为5.4秒，主频为15赫兹，l1模约束阈值函数由成像结果最大值的5％逐渐减小为1％；设置初始成像结果为0进行逆时反偏移计算模型数据，与观测数据相减获得第一数据残差；将所述第一数据残差由共炮点道集变换为共偏移距道集，并分离出反射波场和绕射波场。

设置反射波场加权函数等于0，根据此时的第二数据残差进行迭代反演，输出最终成像结果，如图5所示。从成像结果上看，采用本发明的绕射波成像方法，相对于常规绕射波逆时偏移成像结果(如图3所示)，压制了成像噪音，绕射波能量收敛，振幅更加均衡，提高了地下非均质构造的成像分辨率。

设置反射波场加权函数根据此时的第二数据残差进行迭代反演，得到的成像结果如图6所示。采用本发明的成像方法，相对于常规最小二乘逆时偏移成像结果(如图4所示)，对盐丘下的断层、孔洞等构造成像更加清晰，提高了对地下的所有构造的成像精度。

图7为前例的当加权函数为0和加权函数时，本发明的方法与其他两种成像方法结果的波数谱对比。本发明的成像结果的波数谱相对于常规绕射波成像结果的波数谱，增强了高波数信息，补偿了非均质构造的成像能量。由于绕射波能量较弱，常规最小二乘逆时偏移方法结果中仅含有丰富的中低波数信息，缺少高波数信息，即其成像结果中非均质构造的成像能量较弱。本发明的全波场成像结果的波数谱相对于常规最小二乘逆时偏移成像结果的波数谱，频带更宽，高波数能量更强，对地下所有构造都准确成像。

图8为前例中当加权函数为0和加权函数时，与常规最小二乘逆时偏移方法结果的归一化数据残差收敛曲线对比。常规最小二乘逆时偏移方法的数据残差随着迭代次数的增加收敛速度变慢，而本发明的方法的第二数据残差随迭代增加仍能继续快速收敛。因此，本发明方法相对与现有技术方法，能够改善地下的孔、缝、洞及断层等非均质构造的成像精度，同时能够对地下所有构造高精度成像，对碳酸盐岩储层的勘探具有重要意义。