基于切换控制的长航时惯性导航系统阻尼切换方法与流程

本发明涉及导航、制导与控制技术领域，具体涉及一种基于切换控制的长航时惯性导航系统阻尼切换方法。

背景技术：

惯性导航系统由于能够实时地为载体提供位置、速度、姿态等导航定位信息，在陆、海、空、天各类载体中广泛应用。从控制系统角度来看，惯性导航系统是一个临界稳定的系统，在误差源激励下，系统输出的导航信息中会产生振荡的误差。对于长航时惯导系统，减小振荡误差的有效方法是在惯导系统中引入阻尼。但阻尼的引入会破坏惯导系统原有的舒拉调谐条件，使得载体在机动运行时，系统输出产生误差。为了解决这一问题，惯导系统需要在无阻尼和阻尼状态间进行切换：当载体处于非机动运行时，惯导系统工作在阻尼状态，减小振荡误差带来的影响；当载体处于机动运行时，惯导系统工作在无阻尼状态，减小机动带来的误差。传统方法的切换规则是对加速度设定一个阈值，根据加速度相对阈值的大小来进行切换。这种方法可能会使惯导系统在阈值附近出现频繁切换的现象，从而影响系统性能。为了减小切换时产生的超调，传统方法仅通过设计不同的阻尼网络或对误差进行补偿来改善性能，超调衰减时间长，定位精度提升小。

技术实现要素：

有鉴于此，本发明提供了一种基于切换控制的长航时惯性导航系统阻尼切换方法，能够有效减小惯性导航系统在阻尼切换时的超调量，提高了惯性导航系统的导航定位精度。

本发明的基于切换控制的长航时惯性导航系统阻尼切换方法，包括如下步骤：

步骤1，建立考虑阻尼状态和非阻尼状态的惯性导航系统的数学模型为：

其中，σ(t)是阻尼状态与无阻尼状态的切换律，σ(t)＝1代表阻尼状态，σ(t)＝2代表无阻尼状态，t0是初始时间，x0是初始状态，t是时间；aσ(t)(t)为惯性导航系统的系统矩阵，aσ(t)(t)＝{a1(t),a2(t)}，a1(t)为阻尼状态系统矩阵，a2(t)为无阻尼状态系统矩阵；bσ(t)(t)为惯性导航系统的输入矩阵，bσ(t)(t)＝{b1(t),b2(t)}，b1(t)为阻尼状态系统输入矩阵，b2(t)为无阻尼状态系统输入矩阵；cσ(t)(t)是惯性导航系统输出矩阵，cσ(t)(t)＝{c1(t),c2(t)}，c1(t)为阻尼状态系统输出矩阵，c2(t)为无阻尼状态系统输出矩阵；x(t)为惯性导航系统的系统状态；dw为惯性导航系统的系统干扰矩阵；

u(t)是惯性导航系统的控制输入，u(t)＝-kσ(t)(t)x(t)，kσ(t)(t)为反馈控制矩阵，kσ(t)(t)＝{k1(t),k2(t)}，k2(t)为无阻尼状态下的反馈控制矩阵，k2(t)＝-1；k1(t)为阻尼状态下的反馈控制矩阵，其中，r^-1(t)为控制加权矩阵的逆，p(t)由riccati方程解得，上标t表示转置；

步骤2，根据设置的切换律，利用步骤1建立的惯性导航系统的数学模型实现阻尼切换。

进一步的，所述切换律为：根据惯性导航系统的加加速度相对于设定阈值的大小来进行阻尼切换。

进一步的，对惯性导航系统的加加速度进行小波分解，得到小波系数，对小波系数设定一个阈值，根据小波系数相对其阈值的大小进行阻尼切换。

进一步的，采用daubechies小波进行小波分解。

有益效果：

(1)本发明避免了传统方法简单地通过加速度将惯性导航系统的阻尼状态和无阻尼状态进行区分和切换，利用建立的惯性导航系统数学模型来考虑惯性导航系统的阻尼状态和无阻尼状态切换问题，并利用反馈控制和最优控制理论，通过状态反馈使惯性导航系统的性能指标最优，达到使系统在切换时超调量最小的目的，提高了系统导航定位精度。

(2)本发明利用加加速度与设定阈值的大小作为切换律来进行阻尼切换，较传统的利用加速度实现阻尼切换，能够避免载体以加速度设定阈值航行时，阻尼切换系统频繁切换导致系统不稳定的问题，并且，以加加速度为指标来进行阻尼切换，可以更早的检测到载体运动状态的变化，相对于传统方法能够实现阻尼的提前切换，增加了惯性导航系统的稳定性，提高了系统导航定位精度。

(3)本发明使用的小波算法实时对加加速度进行检测，可以更准确地判断载体运动状态，进而确定更为精确的切换时间，进一步提高惯性导航系统的定位精度。

附图说明

图1为基于切换控制的长航时惯性导航系统阻尼方法的系统框图；

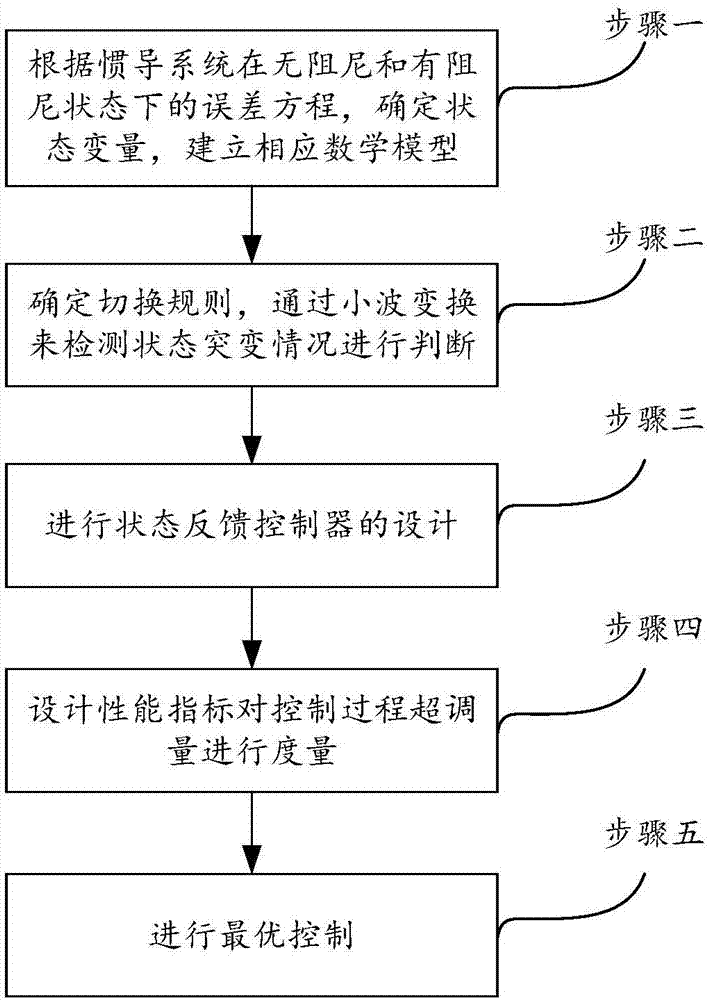
图2为基于切换控制的长航时惯性导航系统阻尼方法的流程图；

图3为状态反馈框图。

具体实施方式

下面结合附图并举实施例，对本发明进行详细描述。

本发明提供了一种基于切换控制的长航时惯性导航系统阻尼切换方法，通过建立惯性导航系统数学模型并利用状态反馈控制器实现惯性导航系统的最优控制，减小切换过程中的超调量，有效提高了惯性导航系统的精度。

本发明的阻尼切换原理是：根据惯性导航系统阻尼与无阻尼状态的特点，建立基于切换控制的惯性导航系统阻尼与无阻尼状态的状态空间数学模型。使用小波变换判断载体运行状态进行切换，通过设计状态反馈控制器，并选择与超调量有关的性能指标，通过状态反馈使性能指标达到最优，从而达到减小超调量的目的，系统框图如图1所示。

具体切换流程如图2所示，包括以下步骤：

步骤1，根据惯性导航系统在阻尼和无阻尼状态下的误差方程，确定状态变量为其中，δve是东向速度误差，δvn是北向速度误差，是纬度误差，φe、φn、φu分别是东、北、天向误差角；建立基于切换控制的惯性导航系统的数学模型为：

其中，σ(t)是阻尼状态与无阻尼状态的切换律，σ(t)＝1代表阻尼状态，σ(t)＝2代表无阻尼状态，t0是初始时间，x0是初始状态，t是时间；aσ(t)(t)为惯性导航系统的系统矩阵，是时间的分段函数，aσ(t)(t)＝{a1(t),a2(t)}，a1(t)为阻尼状态系统矩阵，a2(t)为无阻尼状态系统矩阵；bσ(t)(t)为惯性导航系统的输入矩阵，是时间的分段函数，bσ(t)(t)＝{b1(t),b2(t)}，b1(t)为阻尼状态系统输入矩阵，b2(t)为无阻尼状态系统输入矩阵；cσ(t)(t)是惯性导航系统输出矩阵，cσ(t)(t)＝{c1(t),c2(t)}，c1(t)为阻尼状态系统输出矩阵，c2(t)为无阻尼状态系统输出矩阵；x(t)为惯性导航系统的系统状态；dw为惯性导航系统的系统干扰矩阵；u(t)是惯性导航系统的控制输入，具体表达形式为：

其中，ωie为地球自转角速度，为纬度，r为地球半径，g为重力加速度；和分别为东向和北向加速度计误差，εe，εn和εu分别为东向、北向和天向陀螺漂移。

步骤2，确定切换律，可以采用传统的以加速度为切换规则的切换律，也可以采用本实施例提出的以加加速度为切换规则的切换律。

考虑到惯性导航系统在状态切换时刻，加速度大小无突变，但加加速度会产生突变，因此，可以以加加速度为依据，利用加加速度与设定阈值的大小判断载体的运行状态，从而可以更早的检测到载体运动状态的变化，相对于传统的以加速度为依据的方法能够实现阻尼的提前切换，增加了惯性导航系统的稳定性，提高了系统导航定位精度。

其中，可以利用小波变换对加加速度进行突变性检测，可快速准确地检测到状态的改变，确定更为精确的切换时间。具体的，对惯性导航系统的加加速度采用daubechies小波分解，得到其小波系数。当加加速度没有显著变化时，小波系数没有明显变化；当加加速度有突变时，对应时刻的小波系数会有明显的尖峰，故可对小波系数设定阈值来检测是否存在加加速度突变，从而进行切换。

步骤3，设计状态反馈控制器，对惯性导航系统的状态进行反馈控制，减小惯性导航系统在阻尼状态与无阻尼状态切换时产生的超调量。

设计的状态反馈控制器如图3所示。

具体的，状态反馈控制器的控制输出信号即为u(t)，且

u(t)＝-kσ(t)(t)x(t)

其中，kσ(t)(t)为反馈控制矩阵，kσ(t)(t)＝{k1(t),k2(t)}，k2(t)为无阻尼状态下的反馈控制矩阵，k1(t)为阻尼状态下的反馈控制矩阵。

对于无阻尼状态来说，k2(t)＝-1；对于阻尼状态来说，u(t)＝-k1(t)x(t)，k1(t)为需要设计的反馈控制矩阵。将u(t)＝-k1(t)x(t)代入基于切换控制的惯性导航系统的数学模型中，可得到闭环系统的状态变量模型为

步骤4，在阻尼状态与无阻尼状态切换过程中所有状态会产生超调，因此需要设计性能指标对控制过程的超调量进行度量，对控制的稳态误差也要进行度量，选取性能指标为：

其中，上标t表示转置；q是状态加权矩阵，r是控制加权矩阵，t1是切换初始时刻，tf是切换结束时刻；q和r都可根据要求进行调整。

步骤5，对加入反馈控制器后的惯性导航系统进行最优控制，最优控制的哈密顿函数h为：

根据riccati方程即可求解出最优控制u^*(t)，其中，riccati方程为：

则可以得到最优控制为：其中，r^-1(t)为控制加权矩阵的逆，p(t)可由riccati方程解得。

然后结合状态反馈u^*(t)＝-k1(t)x^*(t)即可得状态反馈矩阵为：

故按照状态反馈矩阵通过状态反馈即可使切换过程性能指标达到最小，从而达到减小超调量的目的，实现最优控制。

综上所述，以上仅为本发明的较佳实施例而已，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。