基于大气变量瞬变扰动方程组的数值天气预报模式系统的制作方法

本发明涉及气象学的技术领域，尤其涉及数值天气预报业务部门对日常使用的原始方程组数值天气预报模式的改革。本发明基于扰动方程组的区域模式可应用于临近(1～12小时)和短期(1～3天)的各种极端天气事件的预报和为环境部门制作异常环境(如雾、霾和沙尘暴)预报，扩展的大范围和全球扰动方程组模式可应用于短期(1～3天)、中期(4～9天)和延伸期(10～30天)的各种极端天气事件和异常天气过程，以及热带风暴(台风和飓风)路径的预报。

背景技术：

早在两千多年前，我们的祖先就为我国的农耕作业总结出了年循环的24个节气和72候。每个节气有确定的气候学意义。什么节气就应该出现那个季节的气候。如果“小雪”节气里发生寒冷和下大雪，而“大雪”节气里偏暖和下雨，前者偏冷和后者偏暖都是发生了异常天气或极端天气。24个节气的年循环气候早就被人们所认识和利用了。人们要预报的是相对正常气候的偏差，即异常天气现象或极端天气事件。24节气和72候可以称为我们祖先发明的古代“气候钟”。

构造一个现代“气候钟”。随着近百年的气象仪器观测发展，很多气象观测站每天有4个时次，甚至24个小时的观测记录。原始方程数值模式也可以把来自卫星、雷达、探空、飞机和自动气象站观测的要素同化起来，形成覆盖全球的所谓大气再分析资料。有了如此多的资料，我们就可以得到覆盖全球从地面到高空对流层-平流层的大气格点资料库。对每个格点上的M年历史资料做同一天文时刻的平均就得到了那个点上，那个天文时刻的气候。这个瞬变气候是客观存在的，它是太阳辐射与下垫面条件共同作用达到动力与热力平衡下的定常态。于是，最大的瞬变气候变化是每天24小时的要素变率，称为瞬变气候的日循环。其次是日与日之间的气候变化，称为瞬变气候的季节循环。这样，年循环的瞬变气候场包含24个时次/天×365天＝8760个时次。于是，我们又构造了一个现代“气候钟”，它有日循环24个刻度的小时指针和季节循环365天刻度的天文日指针，它们指向的8760个时刻有各不相同的气候图画。这些图画是要认识的，不需要预报。

两项分解的扰动天气图。用观测大气变量减去它们对应的气候分量后的天气图称为扰动天气图。在2012年专利(钱维宏，ZL201210134358.4)提出的瞬变扰动天气图中，它是四项分解后的最后一项扰动量绘制的天气图。现在提出的是两项分解后的扰动部分绘制的天气图。四项分解后的扰动天气图与两项分解后的扰动天气图相似，但意义不同。后者的天气图有明确的物理含义。

数值模式预报未来天气。当前观测的和历史观测的大气变量反映的是已经过去了的大气运动状态和天气事件。由当前和历史观测大气变量绘制的天气图也已成历史天气图了。只有未来的天气图才能应用于天气预报。计算机计算的数值天气预报就是让天气走在了时间的前面。数值天气预报是用数学方法和计算机工具解一套大气流体运动的方程组，得到未来时刻的大气运动估计值。

原始方程组模式的问题。半个多世纪以来，数值天气预报采用的方程组称为大气运动原始方程组。大气运动原始方程组的突出特点是，方程中的变量气压(位势高度)、温度、湿度、风等代入方程组的是直接的或原始的观测值(或再分析值)。根据两分量分解的原理，大气原始观测值中包含瞬变气候分量和相对扰动分量。正像我们的祖先早就知道的那样，正常的24节气对应的气候是不需要预报的。同样，我们定义的年循环8760个时刻的气候也是不需要预报的。可是，现在的欧洲、日本、美国和中国的所有全球业务预报模式和像美国WRF那样的区域通用模式输入的初始场中包含了瞬变气候场，并且需要对气候做预报。如果用一个时刻的瞬变气候场代入一个理想的原始方程组数值天气预报模式，则这个模式预报的第2天、第3天，甚至第10天的结果应该是那天的瞬变气候场，但预报的结果会出现与瞬变气候场的偏差，即气候漂移和新的扰动。新的扰动就是虚假的极端天气预报(即谎报)，气候漂移是指模式预报的结果偏离了正常气候钟上的气候循环。

欧洲中心的数值天气预报。当前全球最好的原始方程组模式是欧洲中心的中期数值天气预报模式。它在初始资料同化、模式物理过程参数化和动力过程等方面都是世界领先的，但预报水平也遇到了瓶颈问题，比如，大降水预报可用性为2～3天，常常预报的降水位置比实况偏北、偏东，传统天气图上的环流平均预报为6天。这些位置偏移和时效限制很大程度上来源于模式对气候也做了预报。

模式引进“参考大气”的概念。模式要能长期预报，最大的问题是要确保计算稳定性。在原始方程组的非静力平衡模式中，通常引进“参考大气”的概念。一般的做法是令参考大气满足“静止”或“静力平衡”的条件，且模式大气不要太“远离”参考大气状态。在美国的MM5模式中，取一仅随高度变化的定常廓线为“参考大气廓线”；在法国的MESO-NH模式中，则取初始时刻的水平平均廓线为“参考大气廓线”，这样，起报时间不同，对应的“参考大气廓线”也不同，“部分地”考虑了“参考大气廓线”随时间的变化；在美国NCAR的“SISL”模式中，取温度为定常的“参考大气廓线”；在中国气象局的Grapes模式中取等温(常数)大气为参考大气。引入“定常参考大气”的重要目的是消除垂直运动方程中满足静力平衡的分量，使垂直运动方程中重力与气压梯度力之间由“大项平衡”变为“扰动小项平衡”，使之降低与方程中其它项的“量级差”，从而有效地提高垂直运动方程的计算精度。由于这些等温大气是人为的，因此得到的相对气压扰动、温度扰动和位温扰动不是唯一的，也缺少物理含义。那么，由此得到的这样三个扰动量和三个原始风分量在一起描述的系统也难以描述真实的天气系统。这样的三个扰动量和三个原始风分量进入一个方程组模式会使得预报发生不稳定。

区域偏差中尺度谱模式。另外一种模式称为偏差(perturbation)模式(Juang,2000)，也称为中尺度谱模式(MSM)。这是一个与全球谱模式嵌套的中尺度偏差谱模式。它的偏差是初始观测值相对全球大模式的偏差。模式预报的是这个偏差的未来状况。显然，这个偏差模式的预报会受到来自全球原始方程模式误差的影响和中尺度模式本身误差的影响。同时，中尺度模式在与全球模式嵌套的时候，它们之间边界的处理会引入新的误差。更关键的是，中尺度谱模式预报的这种偏差系统没有物理含义。所以，偏差模式预报产品还得再回到总场变量上来。

瞬变扰动方程组模式。寻找数值天气预报模式的新出路，只有两个方面的创新努力。一是怎样找到一个最有物理意义的参考大气？对它的创新就是年循环的24个时次/天×365天＝8760个时次的现代气候钟参考大气。这个大气是一定存在的，是唯一的，是不需要预报的。二是怎样得到一个能够利用瞬变参考态大气又直接预报出指示极端天气事件种类和落区的动力学方程组模式？对它的创新就是大气变量瞬变扰动方程组数值天气预报模式，简称瞬变扰动方程组模式。对瞬变扰动方程组模式的初始扰动场和预报的扰动场，扰动变量之间是满足静力平衡和地转平衡动力学关系的，所以扰动变量之间的动力学关系是清楚并有物理意义的。

全球一层涡度瞬变扰动方程模式。到目前为止，真正有物理含义的大气扰动模式只是一层的全球扰动涡度谱模式(Qian等,2014；Huang等,2015)。这个一层扰动涡度谱模式可用于台风和飓风的路径预报。扰动模式所在的层次确定在台风或飓风所在的最大扰动涡度层和最小扰动散度层上。在模式预报的过程中，模式层的位置是固定的。所以，它是一个玩具模式，只能预报2～3天。但它能够提前2～3天预报出当前业务(原始方程组)模式常常难以预报的那些突然转向的台风异常路径。原因是一层扰动模式中包含了瞬变气候引导气流的作用，也包含了相邻多个扰动系统之间的相互作用，但不能包含不在这个高度层上扰动系统的相互作用。所以，长时间台风异常路径预报的出路还需要发展多层的瞬变扰动方程组模式。

目前国内外业务部门的数值天气预报模式的不足可以归纳为下列两点：

1、当前大气变量原始方程组模式的数值天气预报系统中输入的初始场仅包括实时观测的瞬时大气变量值，没有考虑历史资料对未来大气运动的影响。而实际上，未来几小时和未来几天的天气变化不但与当前瞬时变量空间分布有关，也与过去几个小时和过去几天的变量变化，甚至更长时间的大气变量的演变规律有关，这些规律就是每天24小时的气候日循环和365天的气候年循环。

2、现有技术的大气变量原始方程组模式的数值天气预报系统的产品对极端天气事件落区定位和对异常天气过程的指示能力较弱。而极端天气事件，如发生暴雨和龙卷的落区一定是大气中逐渐积累的异常或扰动能量迅速释放的结果。大气变量原始方程组模式产品难以凸显这些极端天气事件的扰动特征。

技术实现要素：

本发明要解决的技术问题是设计一种预报准确率更高、且能够预报各种极端天气事件强度和落区的一种基于大气变量瞬变扰动方程组数值天气预报模式系统。

本发明采用如下技术方案解决上述技术问题：设计一种基于大气变量瞬变扰动方程组数值天气预报模式系统，包括：

大气变量数据收集处理子系统、数值天气预报模式子系统和数值天气预报结果输出子系统；

所述大气变量数据收集处理子系统包括大气变量瞬变气候场的计算：用历史观测或再分析的全球或区域范围的位势高度、温度、风和湿度资料，做同一个天文时刻的多年平均，从而得到瞬变的全球或区域空间网格点上的气候值，所有网格点的瞬变气候值构成了多变量瞬变气候场，年循环的瞬变气候场有24个时次/天×365天＝8760个时次；所述大气变量瞬变气候场至少利用历史30年或以上的大气变量的时间序列进行计算。而且每隔一段时间，如1～2年后，对瞬变气候场增加或延长观测资料更新一次。

所述一种基于大气变量瞬变扰动方程组数值天气预报模式的形成过程如下：把大气变量值分解成瞬变气候值和瞬时扰动分量两个部分，则大气变量瞬时扰动场等于当前观测或历史观测或再分析的全球或区域同时刻空间网格点大气变量的总场减去所述大气变量的瞬变气候场，即

分别为：西风扰动u′等于总西风u与气候西风的差；南风扰动v′等于总南风v与气候南风的差；上升气流扰动w′等于总上升气流w与气候上升气流的差；

分别为：气压扰动π′等于总气压π与气候气压的差；水汽扰动q′等于总水汽q与气候水汽的差；温度扰动T′等于总温度T与气候温度的差；这里认为瞬变气候量和满足温度与气压之间的静力平衡关系；

由上述关系获得如下大气变量瞬变扰动方程组：

其中，

上述6个方程即为大气变量瞬时扰动方程组，如果大气变量u,v,w,π,T和q用A来表示，有：

即大气扰动分量A′等于总量A减去瞬变气候量于是，上述6个大气变量瞬时扰动方程都有下列时间倾向形式：

公式(10)等号右边最后一项是大气变量瞬变气候倾向，是已知的，现在需要计算的是大气变量总场A的倾向，或趋势大气变量的每一个瞬时扰动变量的局地变化趋势都是由瞬时总场变量趋势减去瞬变气候变量趋势后得到的；大气瞬变扰动方程组中的m为地图放大因子，F为各个方向上的次网格物理强迫摩擦与耗散项，其他均为气象常用符号(表1)；所述大气瞬时扰动分量和瞬时总场变量作为上述扰动方程组的初始场；

用差分代替大气变量瞬变扰动方程组(3)～(8)中的微分或对方程组(3)～(8)进行谱展开可求得大气变量瞬变扰动方程组未来某个预定时刻的数值解，即获得未来某个预定时刻大气瞬时扰动分量。

所述大气变量数据收集处理子系统包括资料分解器，资料分解器对历史再分析大气变量资料、瞬变气候大气变量资料和现时分析大气变量资料进行分析处理从而获得所述大气瞬时扰动变量。

所述数值天气预报模式子系统包括扰动模式运算器，通过该扰动模式运算器对大气变量瞬变扰动方程组(3)～(8)在有限区域的网格点上求数值解。

所述数值天气预报结果输出子系统同时输出未来某一预定时刻的大气瞬时扰动分量和大气变量总量(即扰动量与气候量的总和)的空间分布图。瞬时扰动分量的空间分布图及其配置关系与各种极端天气事件和异常天气过程有较好的对应关系，用于预报极端天气或中小尺度扰动天气系统的发生；而输出的预报的大气变量总量用于日常的天气预报。

与现有技术相比较，本发明基于大气变量瞬变扰动方程组数值天气预报模式系统具有如下优点：

1、输入本发明的数值天气预报系统的初始场不仅包括实时观测的大气变量瞬时值(模式中的扰动量与气候量的总和)，而且还包括大气变量的瞬变气候值，也就是说，本发明的大气变量扰动方程组模式中的变量要同时包括当前与历史气象信息，历史气象信息就浓缩在本发明定义的瞬变气候场中，该瞬变气候场恰恰是现有国内外所有大气变量原始方程组模式中没有考虑的。同时，扰动模式在时间积分过程中的总场是模式预报瞬时扰动场与瞬变气候场的叠加。

2、大气变量瞬变扰动方程组求解得到的大气变量瞬时扰动场的空间配置结构与极端天气事件强度和落区之间存在着紧密的物理因果关系。在图2a中，大气扰动能量包含在总场的温度和位势高度场中，但难以让天气预报员用肉眼分辨出来。但在图2c中的高度扰动和温度扰动变量分布图中，大气中蕴含的扰动能量的强度分布及其可能要释放的位置就变得很清楚了；也就是说，在地面极端天气事突然发生前，大气中已经有了逐渐发展的扰动变量空间分布的早期信号。因此，本发明的大气变量瞬变扰动方程组模式的预报产品可以用于指示各种极端天气事件的强度和落区。

附图说明

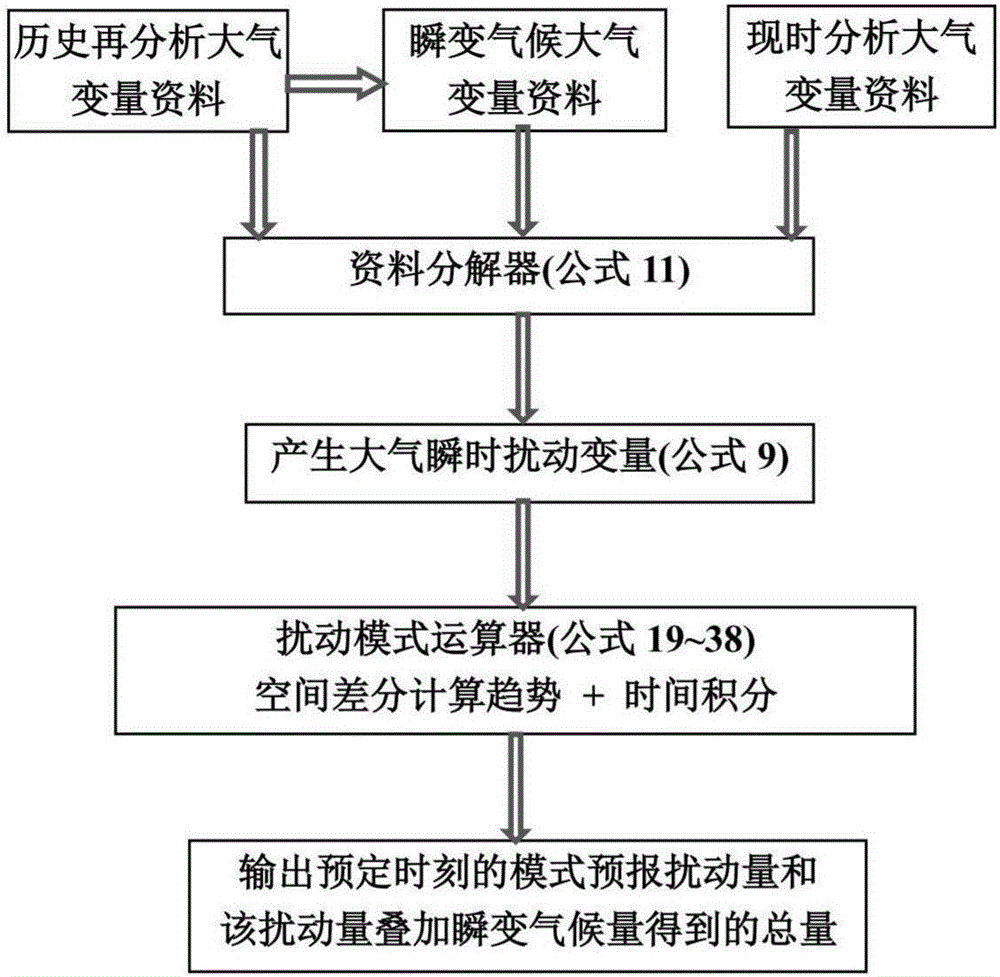
图1是本发明一种基于大气变量瞬变扰动方程组数值天气预报模式系统的运行流程图；

图2是2011年4月28日00UTC(世界时)美国南部不同大气变量沿38^oN和沿1000-50hPa的垂直剖面分布，图中的三角指示龙卷和暴雨发生的位置；其中：(a)中的黑实线为200×10gpm等值线间隔的观测位势高度，阴影为观测总温度每10K间隔；(b)中的黑实线为200×10gpm等值线间隔的气候位势高度；阴影为气候温度每10K间隔；(c)中的黑实线和黑虚线分别为2×10gpm等值线间隔的位势高度扰动和温度扰动分布；(c)中的绿色虚线是上升速度，绿色实线是下沉速度；字母“H/L”和“W/C”指示位势高度扰动“高/低”中心和温度扰动“暖/冷”中心位置(部分引自Qian等,2017)；

图3是2011年4月28日00UTC扰动对流稳定性指数(ACI)分布(阴影，2000℃间隔)与龙卷路径(颜色线)，EF-0至EF-5指示不同等级的龙卷强度(部分引自Qian等,2017)；

图4是对本发明的瞬变扰动方程组(3～8)求数值解时各个大气变量所在网格点的空间分布图的一个实施例；

图5是2016年6月23日发生在江苏省阜宁县的龙卷风位置(符号☆处)及降水量分布(阴影区)，图中的虚线沿119.5°E方向；(a)为00UTC(世界时)或08BJT(北京时)小时降水量，(b)为06UTC(龙卷发生时)小时降水量(阴影，mm h^-1)；

图6是四个时次的原始天气图；其中(a)为2016年6月22日12UTC,(b)为2016年6月22日18UTC，(c)为2016年6月23日00UTC，(d)为2016年6月23日06UTC(龙卷发生时)；位势高度等值线为1000gpm间隔，阴影为温度5K间隔；

图7是四个时次的原始场分解后的扰动天气图；其中(a)为2016年6月22日12UTC,(b)为2016年6月22日18UTC，(c)为2016年6月23日00UTC，(d)为2016年6月23日06UTC(龙卷发生时)；位势高度等值线为5gpm间隔，阴影为温度1K间隔；

图8是四个时次大气变量扰动方程组模式预报的扰动天气图；其中(a)为2016年6月22日12UTC(模式起步时),(b)为2016年6月22日18UTC，(c)为2016年6月23日00UTC，(d)为2016年6月23日06UTC(龙卷发生时)；位势高度等值线为5gpm间隔，阴影为温度1K间隔；

具体实施方式

以下结合附图及实施例对本发明一种基于大气变量瞬变扰动方程组数值天气预报模式系统作进一步的详细说明。

本发明一种基于大气变量瞬变扰动方程组数值天气预报模式系统包括大气变量数据收集处理子系统、数值天气预报模式子系统和数值天气预报结果输出子系统三个部分。

如图1所示，所述大气变量数据收集处理子系统包括资料分解器，该资料分解器对历史再分析大气变量资料、瞬变气候大气变量资料和现时分析大气变量资料进行分析处理从而获得所述大气瞬时扰动变量。本发明的瞬变扰动大气参考态的确定：与现有的中国气象局模式以“常数参考大气”、美国MM5模式以仅随高度变化的定常廓线为“参考大气廓线”、法国MESO-NH模式取初始时刻水平平均廓线为“参考大气廓线”等不同，本发明的参考大气在空间每个格点上都是年循环的24个时次/天×365天＝8760个时次的瞬变气候。为了模式时间积分的步长需要，全球气候场又可以光滑内插成每几分钟的瞬变气候场。

在运行本发明的扰动模式之前，需要用至少M＝30年的每天多时次“历史再分析大气变量资料”代入(12)式，即做时间平均计算，得到“瞬变气候大气变量资料”。随着M数值的增加，所述瞬变气候场就会越接近于太阳辐射与下垫面共同作用下的平衡态气候场；所述瞬变气候场式的计算法只是估算方法中的一种。

大气变量扰动方程组模式运行的开始是要把确定范围内的“历史再分析大气变量资料”(或“现时分析大气变量资料”)和“瞬变气候大气变量资料”输入到“资料分解器”中。分解器需要把历史的或现时的大气资料和瞬变气候资料按照确定的空间(如几公里或几十公里)和时间(几分钟)一一对接起来，用大气变量资料减去瞬变气候资料“产生大气瞬时扰动量”。因此，本发明有别于现有数值天气预报系统的关键之处在于：输入模式的初值不仅有现时分析大气变量资料，而且还包括历史再分析大气变量资料，即使用了历史大气变化规律的有用信息。

所述数值天气预报模式子系统包括扰动模式运算器，通过该扰动模式运算器对大气变量瞬变扰动方程组在有限区域的网格点上求数值解。所述扰动模式运算器大致可分两种计算方法，一是谱展开方法，二是格点方法。

下面先介绍本发明基于大气变量瞬变扰动方程组数值天气预报模式系统的建立过程。

在瞬变扰动方程组模式的6个方程中，方程左端的三个方向风扰动、气压扰动、温度扰动和水汽扰动都是局地变化和倾向，方程右端是全风、全水汽、气候气压、气候温度、气候水汽、气压扰动、温度扰动等的线性和非线性项。

如果大气变量u,v,w,T和q均用A来表示，则瞬时总场变量等于瞬变气候量与瞬时扰动量的总和，有：

其中

为任一个空间网格点上，第y年第d天第t时刻的观测大气变量，称为瞬时总场变量；是由30年以上M个时刻总场变量平均得到的瞬时气候变量；那么就是对应观测时刻的大气瞬时扰动变量。

由上述关系获可得如下大气变量瞬变扰动方程组：

其中，

上述6个方程即为本发明的大气变量瞬时扰动方程组，并有如下关系：

即大气扰动分量A′等于总量A减去瞬变气候量于是，上述6个大气变量瞬时扰动方程都有下列时间倾向形式：

公式(10)等号右边最后一项是已知的大气变量瞬变气候倾向；大气变量的每一个瞬时扰动变量的局地变化趋势都是由瞬时总场变量趋势减去瞬变气候变量趋势后得到的；大气瞬变扰动方程组中的m为地图放大因子，F为各个方向上的次网格物理强迫摩擦与耗散项，其他均为气象常用符号。

上述大气变量瞬变扰动方程组(3)～(8)是非常复杂的偏微分方程，无法求解析解，但可以用差分代替大气变量瞬变扰动方程组(3)～(8)中的微分或对方程组(3)～(8)进行谱展开以能求得大气变量瞬变扰动方程组未来某个预定时刻的数值解，下面给出求瞬变扰动方程组(3)～(8)数值解的一些实现方式。

为了方便起见，本发明给出有限区域格点扰动方程组模式的一个实施例。在垂直方向上采用Lorenz分布格式。在模式顶层k＝K和模式底层k＝0处w(K)＝w(0)＝0，或即在上下边界处垂直速度为0。扰动垂直速度和w′写在垂直整数层上，而其他的变量写在半层上，如图4所示。

在有限区域扰动方程组模式中，水平取C网点格式，所以地图放大因子m＝1。扰动风u′和气候风写在x方向i和i+1格点上，扰动风v′和气候风写在y方向j和j+1格点上。其他变量写在半格点(i+1/2,j+1/2,k+1/2)上(即中间半格点上)。侧边界没有扰动变量流入，但扰动量可以流出。

平流积分方案以x方向上的u′积分为例。(3)～(8)式去除地图放大因子后分别成为：

其中，

在数值积分过程中，网格点上的总量是由瞬变气候值和扰动模式的瞬时扰动分量之和确定的，即：

(13)式右端除了最后瞬变气候倾向项外的倾向差分为：

所有下标格点的空间范围：x方向i＝0～I，y方向j＝0～J，z方向k＝0～K，在此范围外的值为0，水平方向气候场除外；

同样，也可以得到EUⁿi-1/2,j+1/2,k+1/2，EUⁿi+1/2,j-1/2,k+1/2，EUⁿi+1/2,j+1/2,k-1/2等的倾向值；

在有限区域的网格点上，求数值解的时间积分实现方案包括已知的瞬变气候倾向第n+1时步与第n时步的向前有限差分

和对第n+1时步变量与第n-1时步变量之间的时间积分中央差方法

类似的，(14)式右端不包含气候倾向的差分形式：

同样，可得到EVⁿi+1/2,j-1/2,k+1/2，EVⁿi-1/2,j+1/2,k+1/2，EVⁿi+1/2,j+1/2,k-1/2的倾向值；这样，包含已知的瞬变气候倾向的向前有限差分表达

和中央差格式

类似的，(15)式右端暂不考虑瞬变气候倾向项后的差分为：

包含已知的瞬变气候倾向的向前有限差分表达为：

中央差格式为：

类似的，(16)式右端暂不考虑瞬变气候倾向项后的差分为：

包含已知的瞬变气候倾向的向前有限差分表达为：

中央差格式为：

类似的，(17)式右端暂不考虑瞬变气候倾向项后的差分为：

包含已知的瞬变气候倾向的向前有限差分表达为：

中央差格式为：

类似的，(18)式右端暂不考虑瞬变气候倾向项后的差分为：

包含已知的瞬变气候倾向的向前有限差分表达为：

中央差格式为：

本领域的技术人员可以理解，对大气变量瞬变扰动方程组(3)～(8)求数值解还可以采用其他的差分格式，或者对偏微分方程组(3)～(8)进行谱展开使其变换成能够求解的代数方式组，差分格式以及谱展开的方法都是数值天气预报领域技术人员能够掌握的现有技术，这里不再赘述。

本发明的大气变量扰动方程组在形式上虽然类似Juang(2000)的嵌套于全球模式的中尺度偏差模式方程,但天气学意义却是完全不同的。Juang(2000)偏差模式的偏差量等于总量(与扰动方程组模式中的总量相同)减去边界量(全球模式量，即带下标b的量)，即

u′＝u-ub,v′＝v-vb,w′＝w-wb,q′＝q-qb (39)

所以，(39)式中的扰动量(上标有撇的量)与本发明(1)和(2)式中的扰动量是不同的。

在Juang(2000)的偏差模式中，和是满足静力平衡关系的，它们与全球模式场Tb和πb之间存在一个差，即：

于是，总场与和之间的偏差为：

其中下标b为侧边界(大尺度，或外模式)，s为下边界。(42)和(43)中的偏差表示了两层嵌套：内部静力场与外部格点系统嵌套，内部非静力场与内部静力系统嵌套。

本发明的大气变量瞬变扰动方程组模式的时间积分和空间差分采用Juang(2000)中尺度偏差模式的方法。扰动模式的空间分辨率可以达到10公里，甚至5公里和3公里。时间积分可以达到3～5天。大气变量瞬变扰动方程组模式可以应用于暴雨、龙卷等局地强对流性天气扰动系统的预报和多种区域尺度极端天气事件(如热浪和低温)的预报。

图2是2011年4月27日发生在美国南部地区多龙卷爆发的例子。图2a为总(观测)温度(T)和总(观测)位势高度(H)的垂直剖面分布；图2b为瞬变气候温度和瞬变气候位势高度的垂直剖面分布；图2c为温度扰动(T′)和高度扰动(H′)的垂直剖面分布。由于总场高度和总场温度中(图2a)包含了气候高度和气候温度(图2b)，它们都难以指示地面上龙卷和特大暴雨的落区(三角位置)。只是用总高度和总温度减去了气候部分，则它们的差，即高度扰动和温度扰动才能够清楚地表明围绕龙卷和暴雨发生地的上空存在一个正的和一个负的高度扰动中心，以及两正和两负的四个冷暖气团中心(图2c)。四个温度扰动气团可以通过静力平衡关系由高度扰动计算出来。显然，这个扰动天气图上的扰动变量空间结构表达了大气中扰动能量的存在，可以用瞬变扰动方程组模式定量地预报这种扰动在未来的发展。物理意义上，对流层-平流层深厚的大气中这种扰动能量的存在就意味着要发生极端天气事件，即这样的扰动能量会快速地在瞬间释放。

在图2c的扰动变量垂直分布中，龙卷和暴雨发生地上空存在偏暖一侧(红色区)的上升气流和冷区(蓝色区)的下沉气流。下部对流层暖气团与上层平流层冷气团之间的强烈对比形成了垂直方向上的不稳定大气层结结构。这意味着大气中存在巨大的潜在不稳定能量需要释放。同时，对流层大气的左右两侧的冷气团与暖气团也是一种大气的扰动不稳定因素。所以，只要这四个冷、暖气团是存在和发展的，则大气中就会自发释放这样的扰动能量，并出现极端天气。可见，扰动天气图上的扰动变量空间结构不但具有明确的异常大气运动物理含义，同时也能够指示地面极端天气事件的落区。这是扰动天气图优越于传统天气图指示地面极端天气事件的长处。

我们用对流层气团的垂直积分扰动温度量减去平流层相反符号气团的垂直积分扰动温度量，定义一个扰动对流稳定度指数(ACI)。过去很多的垂直对流指标用的是500hPa或600hPa与850hPa之间的温度和风的差。显然，在图2c中500-850hPa气层是在一个扰动气团中，并不能反映不同气团之间的稳定性。图3是2011年4月27日00UTC(世界时)的ACI指数分布和前后3小时内龙卷路径。可见，龙卷的发生与上层冷与下层暖的两个气团有关(红色区)，又与对流层中下部左边冷右边暖的对流层气团对比有关，即龙卷发生在ACI指数从负值到正值过度的地方。

图8是谱方法得到的扰动方程组模式预报结果。两种方法在具体计算的时候依编程人员的经验各有不同的技巧。

“扰动模式运算器”可以按照需要输出不同区域和不同时间点的预报扰动变量资料，也可以用扰动模式预报的扰动变量资料叠加瞬变气候变量资料得到预报的总场变量资料。

用瞬变扰动方程组模式预报的扰动资料可以绘制出扰动天气图(如图8)，也可以计算需要的扰动物理量(如扰动湿涡度和扰动湿散度等)。这些扰动变量和扰动物理量的图像特征可以用于机器学习和图像识别各种极端天气事件。

图5是发生在2016年6月23日06世界时(UTC)，或14北京时(BJT)的地面天气事件。该日山东南部和安徽-江苏北部出现了强降水和局部冰雹，其中江苏省盐城市的阜宁县出现了龙卷，造成了巨大的生命财产损失。2016年6月23日08北京时(00世界时)大降水区位于四省交界的地方，即在山西的东南部、河北的南部、河南的北部和山东的西部(图5a)。6月23日14北京时(06世界时)，大降水区向东南移动到河南的东南部、安徽的北部、山东的南部和江苏的北部(图5b)。强降水发生在33°N至40°N的纬度带上，龙卷发生在强降水区的最南端(五角星处)。强降水、冰雹和龙卷的发生是大气中不稳定扰动能量积累到一定程度释放的结果。我们考察山东南部至苏北北部强降水发生时的南北垂直大气剖面上积累了什么样的扰动能量？扰动方程组模式能否对这样的扰动特征或结构做出预报？

基于大气变量瞬变扰动方程组数值天气预报模式系统，下面给出应用本发明的预报结果与观测的比较：

原始方程组模式是从观测的初始场出发做出未来时刻的各变量预报。图6绘制了2016年6月22日12UTC、22日18UTC、23日00UTC和23日06UTC四个时刻传统天气图上的位势高度(等值线，1000gpm间隔)和温度(阴影，5K间隔)。在位势高度和温度的传统天气图上难以分辨出可以指示龙卷和暴雨的信号。如果用分解法绘制出扰动天气图(图7)，包括高度扰动(等值线，5gpm间隔)和温度扰动(阴影，1K间隔)，则出现了多个高度扰动高低值系统。类似于图2c，在一个高度扰动正中心的下方一定有一个暖的扰动中心，而在其上方一定存在一个冷的扰动中心。类似的，在一个高度扰动负中心的下方一定有一个冷的扰动中心，而在其上方一定存在一个暖的扰动中心。扰动模式起报时刻的初始场(图8a)也是同样。只不过从观测资料垂直扰动层数(图7a)到扰动模式层数转换的过程中，由于层数不同，转换导致了扰动模式初始场(图8a)相对观测资料扰动场(图7a)之间有了偏差。这样的偏差也会影响未来的预报结果。龙卷就发生在近地面暖低压扰动向南发展的过程中。我们考察这样的扰动方程组模式能否预报(或数值积分)下去。

到扰动模式起报的6个小时后，预报结果(图8b)中44°N处对流层上部的低压扰动和39°N处近地面的低压扰动都增强了，于是两个低压上方的暖中心也增强，对流层上部低压下方的冷中心也增强。扰动模式预报的对流层上下部分扰动系统在增强(图8b)与观测资料分析的扰动系统增强(图7b)是完全对应的。这说明扰动模式较好得预报出了扰动系统的增强过程。在40°N附近的上空，对流层低层增暖和其上部降温就形成了类似图2c中的扰动对流不稳定能量。这种扰动对流不稳定能量到23日00UTC(08北京时)继续存在(图7c)，并且也被预报出来了(图8c)。如果这样的扰动对流不稳定能量在当天上午继续增强，那么扰动能量很容易在中午前后释放。结果，苏北北部和山东南部的强降水、局部冰雹和阜宁龙卷就发生在了23日14:00(北京时)前后。图7d中清楚地表明了23日14:00(北京时)近地面温度扰动正值的增加与扰动方程组模式中的近地面温度扰动增加(图8d)一致，只是位置出现了偏差。

所以，大气变量两项分解的扰动空间分布特征(图2c，图7a)比总场变量的空间分布(图2a，图6a)更能具体地指示地面暴雨和龙卷等极端天气事件可能发生的异常信号。当用两项分解的扰动变量代入扰动方程组模式后能够提前18小时预报出对应的大气扰动特征(见图8)。

本发明的大气变量瞬变扰动方程组中所出现的变量非常多，为清楚起见，对本发明出现的所有大气变量详细说明如下：

以上所述仅为本发明的较佳实施例而已，并不局限于本发明描述的例子内容，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，例如，建立在本发明扰动方程组(3)～(8)基础上的全球格点模式和谱展开模式，或建立在本发明扰动方程组(13)～(18)基础上的有限区域格点模式和谱展开模式,均应包含在本发明的保护范围之内。

参考文献

1 Qian WH，Shan XL，Liang HY，Huang J，Leung CH(2014)A generalized beta advection model to improve unusual typhoon track prediction by decomposing total flow into climatic and anomalous flows.J Geophys Res Atmos 119(3)：1097-1

2 Huang J，Du J，Qian WH(2015)A comparison between Generalized Beta-Advection Model and classical Beta-Advection Model in predicting and understanding unusual typhoon tracks in eastern China seas.Wea Forecasting 30：771-792

3 Juang HMH(2000)The NCEP mesoscale spectral model：A revised version of the nonhydrostatic regional spectral model.Mon Wea Rev 128：2329-2362

4 钱维宏，梁卓轩，金荣花，等(2017)扰动变化在强对流天气分析和模式评估中的应用-以苏北里下河地区引发龙卷的扰动系统为例.气象，43(2)：166-180.

5.Qian WH，Leung JCH，Luo WM，Du J，Gao JD(2018)An index of anomalous convective instability to detect tornadic and hail storms.Meteorology and Atmospheric Physics，https：//doi.org/10.1007/s00703-017-0576-z.

6.钱维宏(2015)瞬变扰动天气图和低频扰动天气图制作方法及其在天气预报中的应用.发明专利证书第1647941号，专利号：ZL201210134358.4.