基于卡尔曼滤波的chan-加权质心室内定位方法与流程

本发明涉及基于chan算法的室内定位技术，特别是一种基于卡尔曼滤波的chan-加权质心室内定位方法。
背景技术：
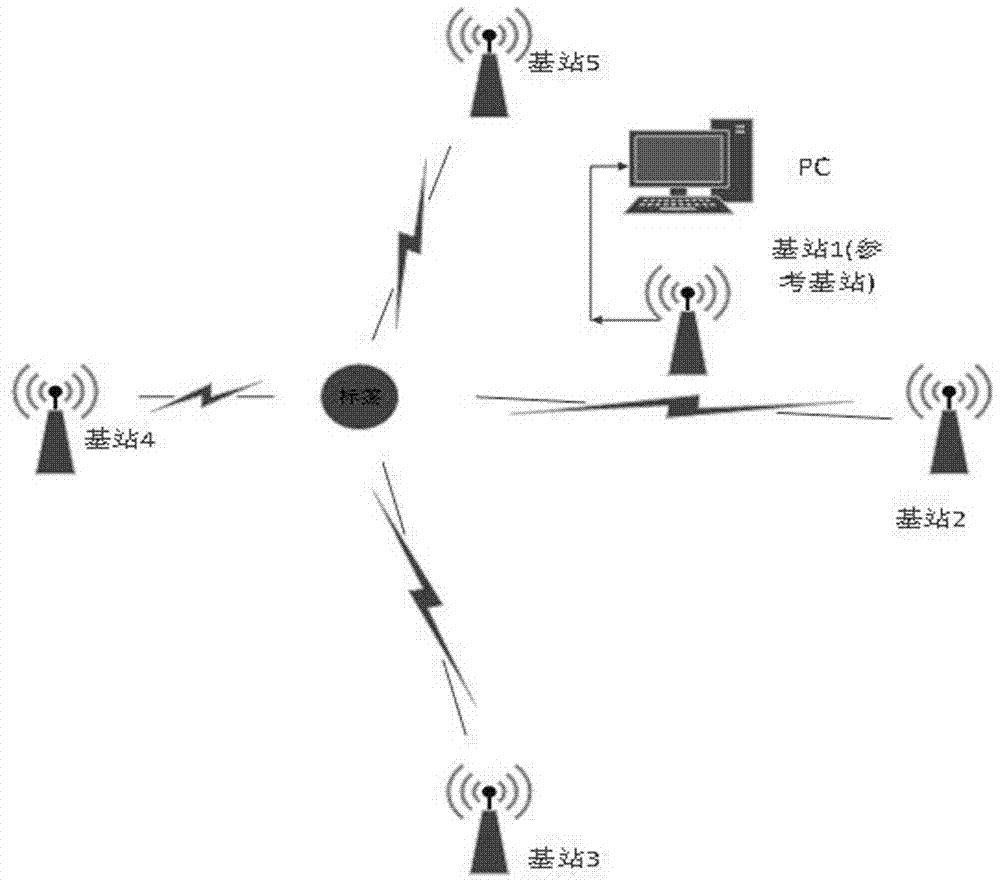
随着无线传感网络和物联网技术的快速发展，人们对于室内定位的需求越来越多，在商场，仓库，超市，医院，监狱等各个场所，对人或物的精确定位有利于提高人员物资的管理效率，在室外环境中，gps能够提供高精度的定位，但是在室内环境下，由于墙壁，高楼等障碍物的遮挡，使得gps难以发挥其优势。因此，很难找到一个适合所有室内场景的高精度室内定位方法。国内外众多学者也针对不同的场景提出了不同的定位方法。针对不同的定位参数，对标签(tag)定位的方法可分为toa(到达时间)，rssi(接受信号强度指示)，aoa(到达角度)，tdoa(到达时间差)等，其中tdoa算法通过测量tag到达两个基站(bs)的时间差方法得到相应的距离差，有效的抵消了单一测距的误差，针对tdoa模型，国内外学者研究了各种定位算法，如jacobi(雅可比迭代)，fang算法，taylor级数展开以及chan算法等。其中fang算法只适用于有限的基站个数，不能使用冗余的测量值，taylor算法需要一个比较精确的初始值，通过迭代得到最终解，若初始位置坐标与真实值误差较大，将导致结果发散。chan算法在测量误差较小且服从高斯分布时，其定位结果的均方根误差能够达到crlb(克拉美罗下界)，但是在室内非视距环境的影响下，会导致测量误差增大，从而使chan算法定位精度急剧下降。为了改善chan算法的定位效果，人们提出了许多减小误差的方法，有的通过nlos的鉴别，判断标签与基站受否为视距传播，对极大影响定位效果的非视距情况进行误差补偿，或者在chan算法求出初始定位后经过无迹卡尔曼滤波以及粒子滤波等方法进行二次定位，同时，有的学者结合chan和taylor算法的优点，利用taylor迭代可以获得较精确的解特点，对chan的定位结果进行修正，但是存在结果不收敛的隐患。技术实现要素：本发明的目的在于提供一种基于卡尔曼滤波的chan-加权质心室内定位方法，以克服现有技术中存在的缺陷。为实现上述目的，本发明的技术方案是：一种基于卡尔曼滤波的chan-加权质心室内定位方法，按照如下步骤实现：步骤s1：通过无线传感器网络测得待定位标签到各基站的距离；步骤s2：将其中一个基站为参考基站，计算所述待定位标签到其他基站与所述待定位标签到参考基站的距离差；步骤s3：将距离差数据输入卡尔曼滤波器进行滤波，得到消除部分噪声干扰的距离差；步骤s4：将经过滤波的距离差和基站坐标信息输入chan算法模型得到初始标签坐标；步骤s5：重复执行n次步骤s1至步骤s4，得到n个初始标签坐标；步骤s6：将n个初始标签坐标输入至一加权质心算法模型确定所述待定位标签最终坐标。在本发明一实施例中，在所述步骤s3中，通过如下方式通过卡尔曼滤波器进行滤波：其中，表示第k-1次距离差向量的估计值，r2，1，r3，1，…rm，1分别为待定位标签其他基站与待定位标签到参考基站的距离差，式中，将参考基站下标记为1，m代表基站总个数。wk表示系统噪声向量，a为状态转移矩阵，pk为第k次估计值的协方差矩阵，qk为系统噪声的协方差矩阵，hk为量测矩阵，zk为测量值向量，rk为测量误差的协方差矩阵。在本发明一实施例中，在所述步骤s4中，通过chan算法模型得到初始标签坐标包括如下步骤：在二维空间定位中，当基站个数m＝3时，由chan算法模型能得到关于初始标签坐标的线性方程组，该方程组方程个数等于未知数个数，能求出唯一解，获取初始标签坐标；在三维空间定位中，当基站个数m＝4时，与二维空间定位相同，能获取初始标签坐标；随着基站个数的增加，方程组的方程个数大于未知数，方程无唯一解，其求解分为两步加权最小二乘法求解：第一次加权最小二乘为：其中，za＝[zpt，r1]t，zp＝[x，y]tr1表示标签到第一个基站的距离，ψ是误差协方差矩阵，ga，h为系数矩阵；以第一次得到的结果为基础进行第二次加权最小二乘：其中，z′a＝[(x-x1)，(y-y1)]t，x，y表示标签坐标，x1，y1是基站1的坐标，ψ′是误差协方差矩阵，g′a，h′为系数矩阵，以获取标签坐标zp。在本发明一实施例中，在所述步骤s6中，还包括如下步骤：步骤s61：计算n个初始标签坐标中各初始标签坐标到各基站的距离差向量；步骤s62：将所述步骤s61所得的每个距离差向量与所述步骤s3所得的滤波后距离差求残差平方和，再开根号作为标签误差，记为error(i)i∈[1，n]，获取n个标签的误差和为：步骤s63：获取每个初始标签坐标的权重向量为：并按从大到小的顺序对权重向量中的元素进行排序；步骤s64：将n个初始标签坐标按照步骤s62获取的标签误差进行从小到大排序；按照误差小的分配高权重，误差大的分配小权重的原则，并采用点乘运算，对坐标进行加权求解。相较于现有技术，本发明具有以下有益效果：本发明提出的一种基于卡尔曼滤波的chan-加权质心室内定位方法，在现有chan定位算法的基础上，采用卡尔曼滤波算法对距离差测量值进行预处理，为chan提供了较精确的初值，并采用加权质心算法对得到的初始定位结果进行附加权重处理，有效抵消了误差的影响，提高了定位精度。附图说明图1为本发明一实施例中室内定位系统结构图。图2为本发明中基于卡尔曼滤波的chan-加权质心室内定位方法的整体算法流程图。图3是本发明一实施例中加权质心算法流程图。图4是本发明一实施例的实施效果图。具体实施方式下面结合附图，对本发明的技术方案进行具体说明。本发明提供一种基于卡尔曼滤波的chan-加权质心室内定位方法，按照如下步骤实现：步骤s1：通过无线传感器网络测得待定位标签距各基站的距离；步骤s2：将其中一个基站为参考基站，计算待定位标签距其他基站与待定位标签距参考基站的距离差；步骤s3：将距离差数据输入卡尔曼滤波器进行滤波，得到消除部分噪声干扰的距离差；步骤s4：将经过滤波的距离差和基站坐标信息输入chan算法模型得到初始标签坐标；步骤s5：重复执行n次步骤s1至步骤s4，得到n个初始标签坐标；步骤s6：将n个初始标签坐标输入至一加权质心算法模型确定待定位标签最终坐标。在本实施例中，在步骤s1中，记标签到各基站的距离即标签到无线传感器网络中第i个基站的距离ri。在本实施例中，在步骤s2中，距离差为标签到其他基站与标签到参考基站的距离差，记为：r2，1，r3，1，…rm，1，式中，将参考基站下标记为1，m代表基站总个数。在本实施例中，在步骤s3中，通过如下方式通过卡尔曼滤波器进行滤波：其中，表示第k-1次距离差向量的估计值，wk表示系统噪声向量，a为状态转移矩阵，pk为第k次估计值的协方差矩阵，qk为系统噪声的协方差矩阵，hk为量测矩阵，zk为测量值向量，rk为测量误差的协方差矩阵。只要给出初始值x1，p1，以及一系列的量测值zk，就可得到经过滤波的距离差。在本实施例中，在步骤s4中，通过chan算法模型得到初始标签坐标包括如下步骤：在二维空间定位中，当基站个数m＝3时，由chan算法模型能得到关于初始标签坐标的线性方程组，该方程组方程个数等于未知数个数，能求出唯一解，获取初始标签坐标；在三维空间定位中，当基站个数m＝4时，与二维空间定位相同，能获取初始标签坐标；随着基站个数的增加，方程组的方程个数大于未知数，方程无唯一解，其求解分为两步加权最小二乘法求解：第一次加权最小二乘为：其中，za＝[zpt，r1]t，zp＝[x，y]t，r1表示标签到第一个基站的距离，ψ是误差协方差矩阵，ga，h为系数矩阵；以第一次得到的结果为基础进行第二次加权最小二乘：其中，z′a＝[(x-x1)，(y-y1)]t，x，y表示标签坐标，x1，y1是基站1的坐标，ψ′是误差协方差矩阵，g′a，h′为系数矩阵，以获取标签坐标zp。在本实施例中，在步骤s6中，还包括如下步骤：步骤s61：计算n个初始标签坐标中各初始标签坐标到各基站的距离差向量：(r2，1，r3，1，…rm，1)；步骤s62：将步骤s61所得的每个距离差向量与步骤s3所得的滤波后距离差求残差平方和，再开根号作为标签误差，记为error(i)i∈[1，n]，获取n个标签的误差和为：步骤s63：根据误差大小，衡量哪一个标签位置更贴近真实值，由此获取每个初始标签坐标的权重向量为：并按从大到小的顺序对权重向量中的元素进行排序；步骤s64：将n个初始标签坐标按照步骤s62获取的标签误差进行从小到大排序；按照误差小的分配高权重，误差大的分配小权重的原则，并采用点乘运算，对坐标进行加权求解。为了让本领域技术人员进一步了解本发明提出的技术方案，下面结合具体实施例进行说明。本实施例中提供一种在二维平面空间，对由uwb无线传感网络组成的定位系统进行定位仿真，系统采用5基站1个标签模型，系统结构图如图1所示，涉及到系统误差以及测量误差时，采用加入标准差为0.2m进行仿真分析。整体算法流程图如图2所示，具体包括以下步骤：步骤s1：通过无线传感器网络测得待定位标签到达各基站的距离；步骤s2：以其中一个基站为参考基站，计算标签到达其他基站与标签到达参考基站的距离差；步骤s3：将距离差数据输入卡尔曼滤波器得到消除部分噪声干扰的距离差；步骤s4：将经过滤波的距离差和基站坐标信息输入chan算法得到初始标签坐标；步骤s5：重复以上步骤n次，得到n个初始标签；步骤s6：利用n个标签坐标进行加权质心算法确定最终标签坐标，算法流程图如图3所示。在本实例中，步骤s1中的标签到各基站的距离即标签到无线传感器网络中5个基站的距离为r1，r2，r3，r4，r5，基站坐标如表1所示。表1坐标x(m)y(m)基站145基站2200基站3020基站4-200基站50-20在本实例中，步骤s2中以基站1为参考基站，标签到其他基站与标签到参考基站的距离差为r2，1，r3，1，…rm，1，其中m＝5。在本实例中，步骤s3中使用卡尔曼滤波算法对s2中所得的测量差进行滤波的过程描述为：式中，其中m＝5，表示第k-1次距离差向量的估计值；wk表示系统噪声向量；a为状态转移矩阵，本实例中为4×4的单位矩阵；pk为第k次估计值的协方差矩阵，qk为系统噪声的协方差矩阵，hk为量测矩阵，本实例中为4×4的单位矩阵，zk为测量值向量，本实例中提供20组量测向量；rk为测量误差的协方差矩阵。本实例中提供20组量测向量zk，初始值x1为第一组量测值，p1为4×4的与初始值x1相关的协方差矩阵，就可得到经过滤波的距离差。在本实例中，步骤s4中基站个数m＝5，方程组的方程个数大于未知数，方程无唯一解，其求解分为两步加权最小二乘法求解。第一次加权最小二乘描述为：其中，za＝[zpt，r1]t，zp＝[x，y]t，r1表示标签到第一个基站的距离，ψ是误差协方差矩阵，ga，h为系数矩阵；接着以第一次得到的结果为基础进行第二次加权最小二乘：其中，z′a＝[(x-x1)，(y-y1)]t，x，y表示标签坐标，x1，y1是基站1的坐标，且该基站1为指定的基站，ψ′是误差协方差矩阵，g′a，h′为系数矩阵，以获取标签坐标zp。在本实例中，步骤s5中，对步骤s1～s4进行3次，得到3个标签的定位坐标。在本实例中，步骤s6中，利用3个标签坐标进行加权质心算法分为以下几步：步骤s61：对3个标签计算3组标签到基站的距离差向量(r2，1，r3，1，…rm，1)，其中，m＝5。步骤s62：将步骤s61所得向量与步骤s3所得的滤波后距离差求残差平方和，再开根号作为标签的误差，记为：error(i)i∈[1，3]，求得3个标签的误差和为：步骤s63：根据误差大小，衡量哪一个标签位置更贴近真实值，由此产生标签的权重向量为并按从大到小的顺序对权重向量内元素进行排序。步骤s64：将3个坐标按照步骤s62求出的误差大小进行从小到达排序，按照误差小的分配高权重，误差大的分配小权重的原则，仿照点乘思想，对坐标进行加权求解。本实例对30个坐标位置进行定位，得到定位结果的rmse约为0.11m，如表2对比了前5组定位效果。表2组数12345真实值(-18，15)(-17.8，14.8)(-17.6，14.6)(-17.4，14.4)(-17.2，14.2)定位值(-17.84，14.79)(-17.78，14.89)(-17.55，14.65)(-17.43，14.41)(-17.14，14.06)以上是本发明的较佳实施例，凡依本发明技术方案所作的改变，所产生的功能作用未超出本发明技术方案的范围时，均属于本发明的保护范围。当前第1页12