一种迈克尔逊干涉仪图像条纹宽度检测方法及系统与流程

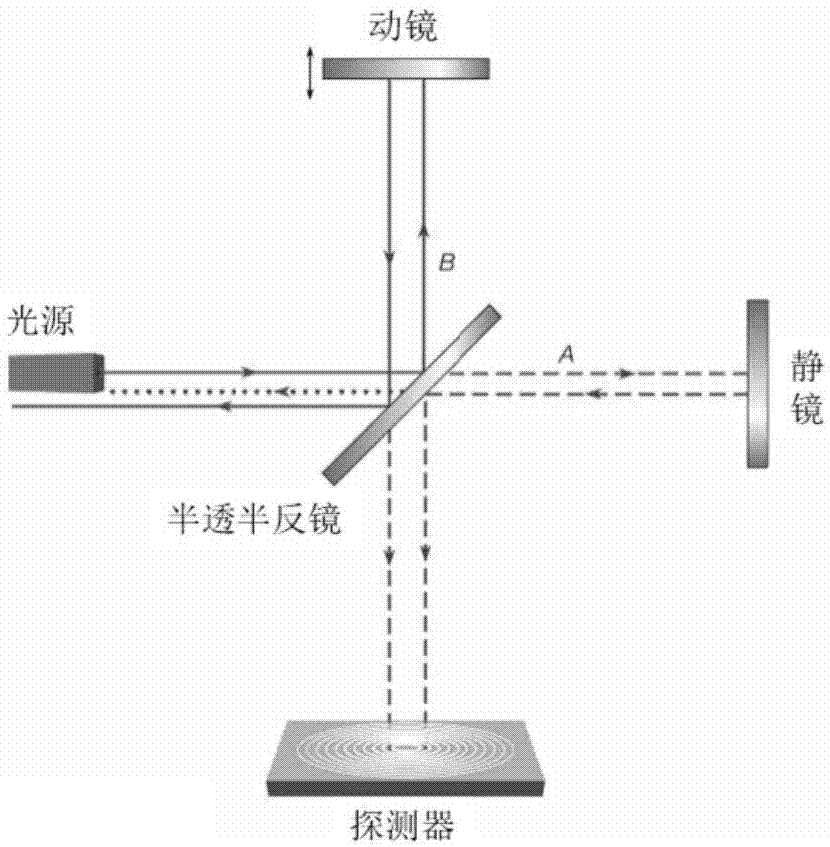
本发明涉及一种通过图像处理算法进行迈克尔逊干涉仪圆环状条纹状态检测的方法。

背景技术：

迈克尔逊干涉仪(英文：michelsoninterferometer)是光学干涉仪中最常见的一种，其原理是一束入射光经过分光镜分为两束后各自被对应的平面镜反射回来，因为这两束光频率相同、振动方向相同且相位差恒定(即满足干涉条件)，所以能够发生干涉。干涉中两束光的不同光程可以通过调节干涉臂长度以及改变介质的折射率来实现，从而能够形成不同的干涉图样。干涉条纹是等光程差的轨迹，若干涉条纹发生移动，一定是场点对应的光程差发生了变化，引起光程差变化的原因。

图1a与图1b分别是迈克尔逊干涉仪的原理图以及所产生的同心圆环图样。通过检测同心圆环的宽度，可以计算出迈克尔逊干涉仪的光程差情况，并反演光谱信息。此外，通过在静态场景下实时监测圆环宽度的变化，可以确认干涉仪状态是否稳定。

传统的干涉仪圆环监测通常需要辅助的计数设备进行，这些仪器可以监测干涉仪同心圆条纹的微小变化，但是此类仪器多数精密复杂，成本较高，在精度要求不高的场合下，使用此类仪器很不方便。

技术实现要素：

本发明的目的是提供一种通过干涉图像自动检测干涉椭圆环宽度的方法，解决使用现有的精密仪器检测条纹宽度成本高且操作复杂的问题，该方法简洁高效，可以用于实时监测迈克尔逊干涉仪圆环条纹状态。

本发明的技术解决方案是提供一种迈克尔逊干涉仪图像条纹宽度检测方法，包括以下步骤：

步骤一：采用自适应二值分割方法，从干涉图样的原始图像上分离亮干涉椭圆环像素，得到前景二值图像；

步骤二：对步骤一获得的前景二值图像进行空洞填充及轮廓优化；

步骤三：检测及标记步骤二优化后前景二值图像中的连通区域；

步骤四：使用形态学运算方法对步骤三检测及标记的连通区域内部进行空洞填充；

步骤五：计算步骤四处理后的每一个被标记的连通区域的中心位置及半长轴及半短轴比例，根据得到的每一个被标记的连通区域的中心位置及半长轴及半短轴比例计算干涉椭圆环中心位置以及半长轴与半短轴比例；

步骤六：根据步骤五的计算结果拟合椭圆及判断拟合后椭圆的亮暗，每个椭圆对应一个编号；

步骤七：依次搜索步骤六拟合的所有椭圆，根据搜索的椭圆亮度获取每个干涉椭圆环的起始椭圆与终止椭圆；即获得每个干涉椭圆环起始椭圆与终止椭圆的位置；根据每个干涉椭圆环起始椭圆与终止椭圆的位置计算干涉椭圆环的宽度。

进一步地，为了避免图像整体亮度不均匀，步骤一中采用分区域16块(4行4列)计算阈值的方法进行分割。

进一步地，步骤二中使用形态学滤波的方法，采用圆形形态学滤波器对步骤一获得的前景二值图像进行空洞填充及轮廓优化；这一过程通过多次的图像“开”、“闭”形态学运算实现。经过这一步骤，大部分杂散点被消除，并且分割的干涉椭圆环区域更加连续，一些缺损和空洞被填充。

进一步地，步骤三通过经典的floodfill算法对步骤二优化后二值图像中的连通区域进行4邻域检测及标记。

进一步地，步骤四具体为：

a1：将步骤三检测及标记的连通区域对应二值图像反转，即前背景互换，经反转后的图像为背景二值图；

a2：通过floodfill算法对背景二值图连通区域进行8邻域标记；

a3：对标记后的背景二值图进行1像素的膨胀运算，将运算结果与前景二值图做差，得到膨胀区域；

a4：在前景二值图连通区域图像上，检查膨胀区域对应像素的连通标记，若某膨胀区域所有标记一致，则认为该背景连通区域为前景连通区域的内部空洞；

a5：将内部空洞像素赋予前景连通区域相同的标记。

进一步地，步骤六包括以下步骤：

a：生成一副与原图同样大小的空白图像，结合干涉椭圆环中心位置以及长短轴比例，根据椭圆公式给空白图像中每一个点赋予一个半长轴或半短轴的值并对每个椭圆编号；

b：求每个编号椭圆上的点对应原始图像像素的平均亮度，根据阈值t判断该干涉椭圆环的亮暗。

进一步地，步骤七中根据椭圆亮度获取每个干涉椭圆环的起始椭圆与终止椭圆的方法为：

若椭圆a的平均亮度小于阈值t且椭圆a-1的平均亮度大于等于阈值t，则椭圆a为一个圆环的起始椭圆；若椭圆a的平均亮度小于阈值t且椭圆a+1的平均亮度大于等于阈值t，则椭圆a为一个圆环的终止椭圆。

本发明还提供一种迈克尔逊干涉仪图像条纹宽度检测系统，其特殊之处在于：包括存储介质及处理器，存储介质存储计算机程序，该计算机程序被处理器执行时，实现上述的方法步骤。

本发明的有益效果是：

1、本发明无需借助其他仪器即可检测迈克尔逊干涉仪的圆环状态；

本发明使用图像处理方法检测迈克尔逊干涉仪的圆环状态，该检测过程可作为干涉仪图像预处理的一部分，无需借助光电计数器等其他仪器。提高了硬件系统的稳定性，降低了成本和体积重量。

2、测量准确性高

本发明基于干涉仪的图像进行圆环检测，可以直接判断圆环状态是否发生变化。由于明暗圆环是迈克尔逊干涉仪的输出信息，因此相比于利用其他仪器间接测量，直接从圆环图像上进行检测准确性更高。此外，本算法充分利用了图像信息中的统计特性，最大程度避免了随机噪声的干扰，进一步提高了检测的准确性。

3、算法运行速度快，可移植性强

本发明设计的算法充分利用了迈克尔逊干涉仪明暗相间圆环图样的的特征，直接寻找圆心并拟合半径。计算过程中不涉及复杂的滑动窗口搜索求解，因此算法运行速度快。此外，算法包含的步骤均为基本的图像处理操作，实现简单，并行性强，也非常容易进行fpga或gpu加速。

附图说明

图1a为迈克尔逊干涉仪的原理图；

图1b为同心圆环图像；

图2为本发明的算法流程框图；

图3a为形态学滤波前的二值分割图；

图3b为形态学滤波后的二值分割图；

图4a为连通区域标记后的图像，不同颜色代表不同连通区域标号；

图4b为将图4a进行形态学处理后的图像；

图5为根据椭圆中心和长短轴比例计算出的不同编号椭圆(对应不同尺寸)；

图6a与图6b分别为暗条纹中间带对应的椭圆以及检测结果信息。

具体实施方式

以下结合附图及具体实施例对本发明做进一步的描述。

本发明能够在低信噪比的迈克尔逊干涉仪图像中自动检测干涉椭圆环的位置和半径，从而计算出干涉仪条纹宽度。其算法如图2所示，具体包括图像预处理、干涉椭圆环参数估计、干涉椭圆环拟合、条纹宽度计算等过程。上述几个过程对应于算法实施的不同阶段，具体按照以下步骤进行实施。

图像预处理：

步骤1：采用自适应二值分割方法，从如图1b所示的低信噪比原始图像上将亮圆环像素分离出来。

寻找适当的阈值，并对图像做自适应阈值分割。阈值的确定采用经典的“大津法”(otsu’smethod)进行。其原理为在图像的统计直方图上寻找最大类间方差的二分类位置。此方法为成熟算法，不在此详述。

由于图像不同区域的干涉环存在亮暗不一致的情况，为了避免图像整体亮度不均匀，因此将整个图像均匀分为16块(4行4列)，在每一块中分别进行自适应二值分割，获取更好的分割效果。

步骤2：对二值分割的结果进行空洞填充及轮廓优化。

由于干涉椭圆环图像噪声通常较大，因此在二值分割结果中存在较多的空洞及毛刺现象。在进行下一步操作之前，使用形态学滤波的方法对二值图像质量进行优化。经过这一步骤，从图3a及图3b的对比可以看出，大部分杂散点被消除，并且分割的干涉椭圆环区域更加连续，一些缺损和空洞被填充。这一过程通过图像“开”，“闭”运算实现，形态学滤波器采用圆形。首先执行半径为r1的闭运算，消除空洞。再执行半径为r2的开运算，消除圆环间的部分随机噪点和毛刺。滤波器参数根据图像尺寸和干涉椭圆环宽度而调整。例如，对于分辨率为1000×1000像素左右且干涉椭圆环宽度在100像素左右的迈克尔逊干涉图像来说，可取r1＝3，r2＝2。

干涉椭圆环参数估计：

步骤3：连通区域检测及标记。

对于上一步优化后的二值图，运行连通区域检测。该步骤可以通过经典的floodfill算法进行4邻域快速标记。使用连通区域标记可以较为完整的检测出中间2-3个间隔较大的干涉椭圆环。利用这几个干涉椭圆环来估计椭圆中心坐标以及长短轴比例。

步骤4：使用形态学运算方法将步骤3标记的连通区域内部空洞填充。

虽然在步骤2中进行了空洞填充的操作，但是由于个别局部区域的亮度不均匀或噪声异常，可能导致在连通区域检测获得的干涉椭圆环内部存在较大的空洞。因此，在连通区域标记后，对干涉椭圆环内部的空洞进行填充以避免影响后续计算的精度。图4a及图4b展示了连通区域标记以及处理后的结果，不同颜色代表不同连通区域标号。

空洞填充的计算过程为：

a1:将步骤3检测及标记的连通区域对应前景二值图像反转，即前背景互换，经反转后的图像为背景二值图；

a2：对背景二值图进行floodfill算法8邻域连通区域标记；

a3：对标记后的背景二值图进行1像素的膨胀运算，将运算结果与前景二值图像做差，得到膨胀区域；

a4：在前景二值图连通区域图像上，检查膨胀区域的标记，若某膨胀区域所有标记一致，则认为该背景连通区域为某前景连通区域的内部空洞；

a5：将内部空洞像素赋予前景连通区域相同的标记。

步骤5：干涉椭圆环中心位置及长短轴比例估计。

在标记的每一个连通区域上，计算每一个连通区域的中心位置，中心位置的计算方法为所有该标记像素点位置的平均值。对中心位置进行筛选，若中心位置的横纵坐标偏离图像中心超过10％，则认为该连通区域标记有误，删除其计算结果。对剩下的连通区域中心位置(xi，yi)，i＝1…n求中位数作为干涉椭圆环中心位置，得到干涉椭圆环的中心位置(xc，yc)

(xc，yc)＝median((x1，y1)，(x2，y2)，…，(xn，yn))

对这些连通区域计算长轴和短轴长度。连通区域的长短轴定义为与其具有相同二阶中心矩的椭圆的长轴和短轴长度。根据长短轴计算的结果，可以求出半长轴ai和半短轴bi的比例，将比例记为ri，

将所有连通区域计算出的比例求取中位数作为椭圆环半长轴和半短轴比例，

r＝median(r1，r2，…，rn)

干涉椭圆环拟合

步骤6：椭圆拟合及亮暗判断。

将与原图同样大小的空白图像上一个点的坐标记为(x，y)，根据椭圆公式，在x轴对应椭圆长轴的情况下，可以得出(x，y)点所在椭圆的半长轴长度a(x，y)为

坐标轴和椭圆长短轴的对应关系在仪器安装好后就已确定。此外，也可以根据上面求解连通区域二阶矩的方式对椭圆的方向进行估计。

根据上面公式可以为图像中每个点赋予一个半长轴的值(为了便于计算可以四舍五入取整数)。用半长轴的整数值作为椭圆编号，并给该椭圆轮廓所在像素赋值，即半长轴为a的椭圆编号为a(根据实际情况，半长轴小于10的像素点一般位于中心亮斑、暗斑内，可以不考虑)。图5展示了不同大小的椭圆，分别具有不同标号，对应不同的半长轴长度。通过求每个椭圆上的点对应原图像素的平均亮度，就可以根据阈值t判断该圆环的亮暗(在图像灰度归一化到[0,1]的情况下，阈值t可以取0.2)。

条纹宽度计算

7、干涉椭圆环条纹宽度计算。

依次搜索所有椭圆，获取每个干涉椭圆环的起始椭圆和终止椭圆序号。具体方法为，若椭圆a的平均亮度小于阈值t且椭圆a-1的平均亮度大于等于阈值t，则椭圆a为一个圆环的起始椭圆；若椭圆a的平均亮度小于阈值t且椭圆a+1的平均亮度大于等于阈值t，则椭圆a为一个圆环的终止椭圆。这样，获取了所有暗环的起始终止位置，就可以计算得到暗环的宽度以及间隔(由于椭圆为同心、同比例，因此通过半长轴或半短轴计算宽度和间隔会得到一样结果)。图6a与图6b展示了暗条纹中间带对应的椭圆，以及根据此检测椭圆条纹宽度等结果信息。