一种多脉冲组合探测的雷达信号快速恢复方法与流程

本发明涉及雷达技术领域，尤其涉及一种多脉冲组合探测的雷达信号快速恢复方法。

背景技术：

雷达是通过发射探测信号并接收目标的反射信号来获取目标信息的一种无线电遥感探测设备。在现有技术中，雷达的工作体制主要可以划分为脉冲和连续波两种工作方式。

在脉冲工作方式下，雷达(也称为“脉冲雷达”)发射脉冲形式的探测信号，之后接收目标的回波信号，脉冲雷达的发射和接收在时间上是先后分开的；在连续波工作方式下，雷达(也称为“连续波雷达”)发射连续波探测信号，与此同时接收目标的回波信号，连续波雷达的发射和接收是同时二[作的。

在脉冲工作方式下，发射探测信号和接收目标回波信号是分时工作，因而收发之间的相互影响比较小，雷达可以发射功率比较大的信号，探测距离可以比较远。然而，由于发射信号时不能接收信号，所以存在探测距离的下限，也就是探测盲区，其大小由发射信号的脉冲宽度决定。在很多情况下，由于探测区域的要求，脉冲宽度有限，要求加大探测脉冲的峰值功率，从而提高发射信号的平均功率，导致发射机设备更为庞大复杂。

在连续波工作方式下，由于连续发射探测信号，使得发射信号的平均功率较大，相对脉冲工作方式而言，其发射信号的峰值功率要小的多，可以采用固态器件、部件方案，实现体积、重量的轻小型化。然而，由于发射和接收信号的工作同时进行，发射和接收通道之间的影响相对较大。为了减少影响保证接收机能够正常工作，一方面要求提高收发通道的隔离度，另一方面对发射机的发射信号功率也要有一定的限制。在这些条件和限制下，导致了连续波雷达的性能受到一定的影响，探测距离比较近。

针对脉冲雷达和连续波雷达的上述缺陷或不足，中科院电子所发明了连续脉冲雷达工作体制，这一新的雷达工作体制借鉴脉冲与连续波雷达的优点，基于发射和接收信号相间隔的方式以一定的间隔连续发射探测脉冲信号，同时在发射脉冲信号之间的时间间隔接收目标的回波信号，以发射时间间隔连续发射设定宽度的探测脉冲信号，在发射的探测脉冲信号之间的脉冲时间间隔接收目标的部分回波信号，再基于部分回波信号恢复完整回波信号。

在该发明中，根据部分回波信号以及时间窗来恢复完整回波信号包括：将所述部分回波信号变换到频域，以得到第一频域信号；将所述时间窗变换到频域，以得到第二频域信号；根据所述第一频域信号和所述第二频域信号，按照下式计算所述回波信号的频域信号：

其中表示卷积运算，yp(ω)是所述第一频域信号，pt(ω)是所述第二频域信号，并且y(ω)是所述回波信号的频域信号；以及将所述回波信号的频域信号反变换到时域，以得到所述完整回波信号。

该发明的信号恢复过程尽管是采用频域快速卷积运算，但计算量仍然非常巨大，不利于实时实现，因此，需要对连续脉冲雷达体制进行改进，在利用连续脉冲雷达体制的优势的同时，降低恢复处理的计算量，存在雷达信号快速恢复方法的需求。

技术实现要素：

本发明的目的在于提供一种多脉冲组合探测的雷达信号快速恢复方法，其能够克服多脉冲编码信号恢复计算量巨大的问题，实现对雷达信号的快速恢复，满足实时雷达信号处理的要求。

为了实现上述目的，本发明提供了一种多脉冲组合探测的雷达信号快速恢复方法。

本发明一实施例提供了一种多脉冲组合探测的雷达信号快速恢复方法，该方法在多脉冲编码时，将多脉冲分为n组，每组m个子脉冲，子脉冲等时宽，采用0度相移的子脉冲，或采用180度相移的子脉冲；在接收解码时，构建接收窗口回波的分组整数系数矩阵，将恢复运算由卷积运算，简化为仅包含加减运算的矩阵和向量内积运算，实现雷达信号的快速恢复。

根据本发明提供的多脉冲组合探测的雷达信号快速恢复方法，该方法包括：

首先，对多脉冲组合编码，将该多脉冲组合信号分为n组，每组m个子脉冲，各个子脉冲等时宽，其中，m＞1，n＞1；

进一步的，在无脉冲发射时为接收窗口，每一个子脉冲时间宽度对应的接收间隔作为1个接收窗口。

其次，构建接收窗口；

进一步的，该构建的接收窗口为：

两个子脉冲之间有1至m-1个与子脉冲宽度相等的接收窗口，每一个子脉冲的完整回波由k个接收窗口组成，k＝m+j-1，j为该组多脉冲全部接收窗口的脉冲宽度的个数。

接着，以设定的时间间隔连续、循环发射各子脉冲信号，并在该时间间隔内通过接收窗口接收对应的回波信号；

进一步的，以设定的时间间隔连续、循环发射各子脉冲信号包括：

发射0度相移的子脉冲，或180度相移的子脉冲。

然后，对接收到的回波信号解码，基于接收窗口构建回波信号的分组整数系数矩阵，将恢复运算由卷积运算简化为仅包含加减运算的矩阵和向量内积运算，得到恢复信号；

进一步的，恢复运算为：

其中，ek为第k个接收窗口的恢复信号，rk，i为恢复矢量，gi为接收窗口信号矢量，ak为噪声加权矢量，n为噪声矢量。

最后，对恢复信号进行归一化处理，得到目标回波信号，实现雷达信号的恢复。

进一步的，对恢复信号进行归一化处理为：

其中为第k个接收窗口的归一化恢复信号，dk为第k个接收窗口的归一化系数。

根据本发明提供的多脉冲组合探测的雷达信号快速恢复方法至少具有如下有益效果：

将恢复运算由卷积运算，简化为仅包含加减运算的向量运算，实现雷达信号的快速恢复，便于实现实时信号处理。

附图说明

通过以下结合附图的说明，并且随着对本发明的更全面了解，本发明的其他目的和效果将变得更加清楚和易于理解，其中：

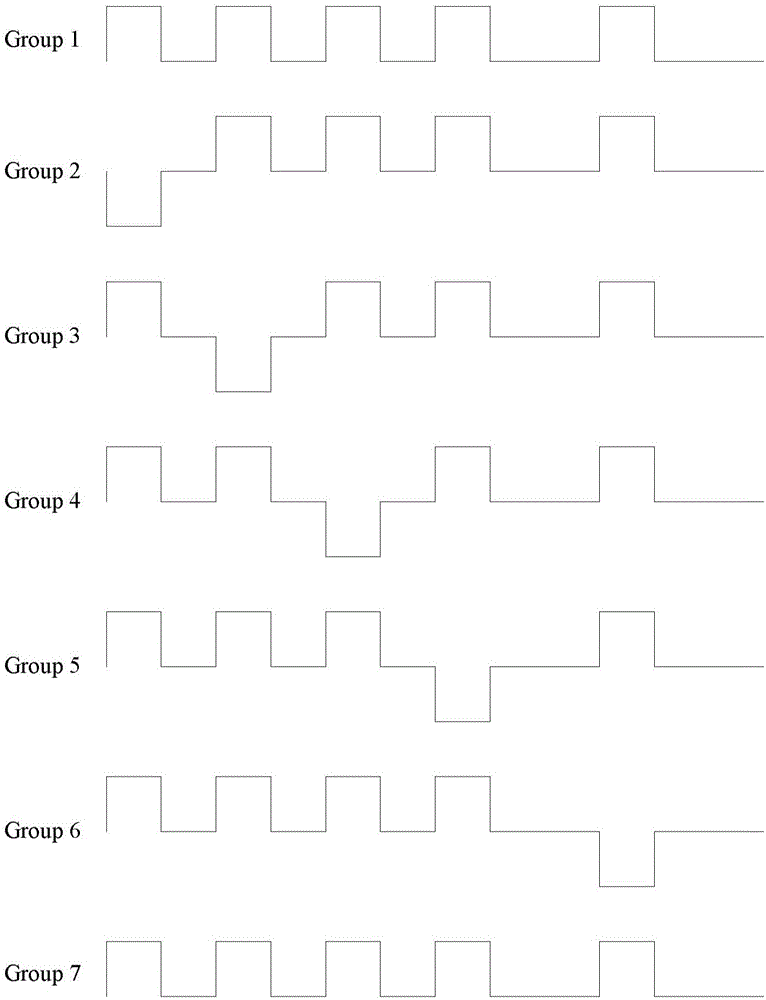
图1是本发明实施例基于n＝7、m＝5、k＝11、j＝7的多脉冲编码的示意图；

图2是本发明实施例基于n＝7、m＝5、k＝11、j＝7的接收窗口的回波信号编码的示意图。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚明白，以下结合具体实施例，并参照附图，对本发明作进一步的详细说明。

本发明一实施例提供了一种多脉冲组合探测的雷达信号快速恢复方法，包括：

对多脉冲组合编码，将该多脉冲组合信号分为n组，每组m个子脉冲，各个子脉冲等时宽，其中，m＞1，n＞1；

一些实施例中，在无脉冲发射时为接收窗口，每一个子脉冲时间宽度对应的接收间隔作为1个接收窗口。

其次，构建接收窗口；

一些实施例中，该构建的接收窗口为：

两个子脉冲之间有1至m-1个与子脉冲宽度相等的接收窗口，每一个子脉冲的完整回波由k个接收窗口组成，k＝m+j-1，j为该组多脉冲全部接收窗口的脉冲宽度的个数。

本实施例中，请参见图1，是设定n＝7、m＝5、k＝11、j＝7时多脉冲编码的示意图。图中，向上的脉冲表示发射0度相移的子脉冲，向下的脉冲表示发射180度相移的子脉冲，无脉冲时表示接收窗口，可以有多个连续的接收窗口，每一个脉冲和接收窗口占用相同的时间宽度。

基于以上实施例，用1表示发射0度相移的子脉冲，-1表示发射180度相移的子脉冲，0表示接收窗口，则图1各脉冲组可以表示为：

第1组多脉冲：101010100100；

第2组多脉冲：-101010100100；

第3组多脉冲：10-1010100100；

第4组多脉冲：1010-10100100；

第5组多脉冲：101010-100100；

第6组多脉冲：101010100-100；

第7组多脉冲：101010100100。

接着，以上述多脉冲编码设定的时间间隔连续、循环发射各子脉冲信号，并在该时间间隔内通过接收窗口接收对应的回波信号；

一些实施例中，以固定时间间隔连续、循环发射各子脉冲信号包括：

发射0度相移的子脉冲，或180度相移的子脉冲。

然后，对接收到的回波信号解码，基于接收窗口构建回波信号的分组整数系数矩阵，将恢复运算由卷积运算简化为仅包含加减运算的矩阵和向量内积运算，得到恢复信号；

一些实施例中，恢复运算为：

其中，ek为第k个接收窗口的恢复信号，rk，i为恢复矢量，gi为接收窗口信号矢量，ak为噪声加权矢量，n为噪声矢量。

基于以上实施例，本实施设每一个子脉冲的完整回波由11个接收窗口组成，分别为：e1、e2、e3、e4、e5、e6、e7、e8、e9、e10、e11，连续脉冲的快速解码恢复方法可以表示为：

其中ek为第k个接收窗口的恢复信号，rk，i为恢复矢量，gi为接收窗口信号矢量，ak为噪声加权矢量，n为噪声矢量。

图2是n＝7、m＝5、k＝11、j＝7接收窗口的回波信号编码的示意图，第m组第n个接收窗口的回波信号表示为g(m，n)，则接收窗口信号矢量gi的转置gi′可以表示为：

g1′＝[g(1，1)g(1，2)g(1，3)g(1，4)g(1，5)g(1，6)g(1，7)]

g2′＝[g(2，1)g(2，2)g(2，3)g(2，4)g(2，5)g(2，6)g(2，7)]

g3′＝[g(3，1)g(3，2)g(3，3)g(3，4)g(3，5)g(3，6)g(3，7)]

g4′＝[g(4，1)g(4，2)g(4，3)g(4，4)g(4，5)g(4，6)g(4，7)]

g5′＝[g(5，1)g(5，2)g(5，3)g(5，4)g(5，5)g(5，6)g(5，7)]

g6′＝[g(6，1)g(6，2)g(6，3)g(6，4)g(6，5)g(6，6)g(6，7)]

g7′＝[g(7，1)g(7，2)g(7，3)g(7，4)g(7，5)g(7，6)g(7，7)]

用ei和噪声ni表示g(m，n)，得到如下的49个表达式：

g(1，1)＝e1+e4+e7+e9+e11+n1；

g(1，2)＝e1+e3+e6+e9+e11+n2；

g(1，3)＝e1+e3+e5+e8+e11+n3；

g(1，4)＝e1+e3+e5+e7+e10+n4；

g(1，5)＝e2+e4+e6+e8+e11+n5；

g(1，6)＝e1+e4+e6+e8+e10+n6；

g(1，7)＝e2+e5+e7+e9+e11+n7；

g(2，1)＝-e1+e4+e7+e9+e11+n8；

g(2，2)＝e1-e3+e6+e9+e11+n9；

g(2，3)＝e1+e3-e5+e8+e11+n10；

g(2，4)＝e1+e3+e5-e7+e10+n11；

g(2，5)＝e2+e4+e6-e8+e11+n12；

g(2，6)＝e1+e4+e6+e8-e10+n13；

g(2，7)＝e2+e5+e7+e9-e11+n14；

g(3，1)＝e1+e4+e7+e9+e11+n15；

g(3，2)＝-e1+e3+e6+e9+e11+n16；

g(3，3)＝e1-e3+e5+e8+e11+n17；

g(3，4)＝e1+e3-e5+e7+e10+n18；

g(3，5)＝e2+e4-e6+e8+e11+n19；

g(3，6)＝e1+e4+e6-e8+e10+n20；

g(3，7)＝e2+e5+e7-e9+e11+n21；

g(4，1)＝e1+e4+e7+e9-e11+n22；

g(4，2)＝e1+e3+e6+e9+e11+n23；

g(4，3)＝-e1+e3+e5+e8+e11+n24；

g(4，4)＝e1-e3+e5+e7+e10+n25；

g(4，5)＝e2-e4+e6+e8+e11+n26；

g(4，6)＝e1+e4-e6+e8+e10+n27；

g(4，7)＝e2+e5-e7+e9+e11+n28；

g(5，1)＝e1+e4+e7-e9+e11+n29；

g(5，2)＝e1+e3+e6+e9-e11+n30；

g(5，3)＝e1+e3+e5+e8+e11+n31；

g(5，4)＝-e1+e3+e5+e7+e10+n32；

g(5，5)＝-e2+e4+e6+e8+e11+n33；

g(5，6)＝e1-e4+e6+e8+e10+n34；

g(5，7)＝e2-e5+e7+e9+e11+n35；

g(6，1)＝e1+e4-e7+e9+e11+n36；

g(6，2)＝e1+e3+e6-e9+e11+n37；

g(6，3)＝e1+e3+e5+e8-e11+n38；

g(6，4)＝e1+e3+e5+e7+e10+n39；

g(6，5)＝e2+e4+e6+e8+e11+n40；

g(6，6)＝-e1+e4+e6+e8+e10+n41；

g(6，7)＝-e2+e5+e7+e9+e11+n42；

g(7，1)＝e1-e4+e7+e9+e11+n43；

g(7，2)＝e1+e3-e6+e9+e11+n44；

g(7，3)＝e1+e3+e5-e8+e11+n45；

g(7，4)＝e1+e3+e5+e7-e10+n46；

g(7，5)＝e2+e4+e6+e8-e11+n47；

g(7，6)＝e1+e4+e6+e8+e10+n48；

g(7，7)＝e2+e5+e7+e9+e11+n49；

解码恢复方法的恢复矢量rk，i分别为：

r1，1＝[1111010]

r1，2＝[-4111010]

r1，3＝[-3011010]

r1，4＝[11-41010]

r1，5＝[111-4010]

r1，6＝[11110-40]

r1，7＝[1111010]

r2，1＝[0000101]

r2，2＝[0000101]

r2，3＝[0000101]

r2，4＝[0000101]

r2，5＝[0000-401]

r2，2＝[000010-4]

r2，7＝[0000101]

r3，1＝[0111000]

r3，2＝[0-411000]

r3，3＝[01-41000]

r3，4＝[011-4000]

r3，5＝[0111000]

r3，6＝[0111000]

r3，7＝[0111000]

r4，1＝[1000110]

r4，2＝[1000110]

r4，3＝[1000110]

r4，4＝[1000-410]

r4，5＝[10001-40]

r4，6＝[1000110]

r4，7＝[-4000110]

r5，1＝[0011001]

r5，2＝[00-41001]

r5，3＝[001-4001]

r5，4＝[0011001]

r5，5＝[001100-4]

r5，6＝[0011001]

r5，7＝[0011001]

r6，1＝[0100110]

r6，2＝[0100110]

r6，3＝[0100-410]

r6，4＝[01001-40]

r6，5＝[0100110]

r6，6＝[0100110]

r6，7＝[0-400110]

r7，1＝[1000101]

r7，2＝[1000101]

r7，3＝[1000-401]

r7，4＝[100010-4]

r7，5＝[1000101]

r7，6＝[-4000101]

r7，7＝[1000101]

r8，1＝[0010110]

r8，2＝[0010-410]

r8，3＝[00101-40]

r8，4＝[0010110]

r8，5＝[0010110]

r8，6＝[0010110]

r8，7＝[00-40110]

r9，1＝[1100001]

r9，2＝[1100001]

r9，3＝[110000-4]

r9，4＝[1100001]

r9，5＝[-4100001]

r9，5＝[1-400001]

r9，7＝[1100001]

r10，1＝[0001010]

r10，2＝[00010-40]

r10，3＝[0001010]

r10，4＝[0001010]

r10，5＝[0001010]

r10，6＝[0001010]

r10，7＝[000-4010]

r11，1＝[1110101]

r11，2＝[111010-4]

r11，3＝[1110101]

r11，4＝[-4110101]

r11，5＝[1-410101]

r11，6＝[11-40101]

r11，7＝[1110-401]

噪声加权矢量ak分别为：

a1＝[1111010-41110101-41101010-41010111-401011110-401111010]

a2＝[00001010000101000010100001010000-401000010-40000101]

a3＝[01110000-41100001-41000011-4000001110001110000011000]

a4＝[100011010001101-400101010-401010001001000011-4000110]

a5＝[001100100-41001001-40010011001001100-400110010011001]

a6＝[010011001001100100-41001001-40010011001000100-400110]

a7＝[100010110001011000-401100010-41000101-40001011000101]

a8＝[00101100010-41000101-4000101100010110001011000-40110]

a9＝[11000011100001110000-41100001-410000110-400011100001]

a10＝[000101000010-400001010000101000010100001010000-4010]

a11＝[1110101111010-41110101-41101011-41010111-401011110-401]

噪声矢量n的转置n′为：

n′＝[n1n2n3n4n5n6n7n8n9n10n11n12n13n14n15n16n17n18n19n20n21n22n23n24n25n26n27n28n29n30n31n32n33n34n35n36n37n38n39n40n41n42n43n44n45n46n47n48n49]

最后，对恢复信号进行归一化处理，恢复出目标回波信号，实现雷达信号的恢复；

一些实施例中，对恢复信号进行归一化处理为：

其中为第k个接收窗口的归一化恢复信号，dk为第k个接收窗口的归一化系数。

本实施例中，对恢复信号进行归一化处理：

其中为第k个接收窗口的归一化恢复信号，dk为第k个接收窗口的归一化系数，其中d1＝d11＝50，d2＝d10＝20，d3＝d4＝d5＝d6＝d7＝d8＝d9＝30。

最终，恢复出目标回波信号之后，就可以如同脉冲雷达或连续波雷达一样，根据需要进行后续的处理工作。

应当注意，为了使本发明的实施方式更容易理解，上面的描述省略了对于本领域的技术人员来说是公知的、并且对于本发明的实施方式的实现可能是必需的更具体的一些技术细节。例如，上面的描述省略了对现有的频域快速卷积算法的一般性描述。应该理解，根据本发明的实施例的n＝7、m＝5、k＝11、j＝7的编码方法和快速解码方法，还可以具有现有的其它参数的编码方法和快速解码方法。上述说明仅仅是示意性的而不是限制性的。

提供本发明的说明书是为了说明和描述，而不是用来穷举或将本发明限制为所公开的形式。对本领域的普通技术人员而言，许多修改和变更都是可以的。

以上所述的具体实施例，对本发明的目的、技术方案和有益效果进行了进一步详细说明，应理解的是，以上所述仅为本发明的具体实施例而已，并不用于限制本发明，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。