一种大地电磁测深曲线的定量优选方法与流程

本发明属于地球物理勘探领域，涉及大地电磁数据处理技术，尤其是涉及针对分布式数据处理后大地电磁测深曲线的定量优选方法。

背景技术：

大地电磁测深法(mt)是在地面上一点或多点同时观测天然变化的、互为垂直的电磁场分量，用以探测地球内部的电性构造。由于其具有野外施工简便、探测深度大等优点，因此该方法在研究深部地质构造、矿产勘查、油气勘探等方面得到了广泛应用。

目前，大地电磁测深由传统的单点观测逐渐向分布式观测发展，以便提高观测效率，同时，分布式观测后的大地电磁数据便于利用多种张量估算方法进行分布式处理。相比单点观测仅能处理一组测深曲线，分布式观测能够从分布式处理后的多组测深曲线中进行优选。

目前有多种张量估算方法来进行大地电磁测深曲线估算，包括：单点处理(sims,etal.,1971)，利用本地站与参考站信号相关而噪声非相关性的远参考处理(gamble，1979，具体参见：gambletd.magnetotelluricswitharemotereference[j].geophysics,1979,81(1):87-94)(下文简称为远参考处理)，利用本地站与参考站磁场相关性的磁场相关远参考处理(varentsov,2003，具体参见：varentsovim.chapter10arraysofsimultaneouselectromagneticsoundings:design,dataprocessingandanalysis[j].methodsingeochemistry&geophysics,2003,40:259-273；张刚，等,2017，具体参见：张刚,庹先国,王绪本,等.磁场相关性在远参考大地电磁数据处理中的应用[j].石油地球物理勘探,2017(6):1333-1343)(下文简称为基于磁场相关远参考处理)，共用磁道处理(张文秀，等，2012，具体参见：张文秀,周逢道,林君,等.分布式电磁探测系统在深部地下水资源勘查中的应用[j].吉林大学学报(地球科学版),2012,42(4):1207-1213.)。对于上述四种数据张量估算，如果在同一测区有n台大地电磁测深仪同时进行分布式观测，对于某一观测点来说，单点处理方式利用本地站的电场数据和磁场数据处理有1组处理结果；远参考处理、基于磁场相关远参考处理利用其它n-1个采集站的磁场数据和本地站的电磁场数据进行处理分别有n-1组处理结果；共用磁道处理利用本地电场和其它n-1个采集站的磁场数据来进行处理，也有n-1组处理结果；那么该采集站所有的处理结果总数为3n-2组，假设分布式观测共有10个采集站，则多达28组处理结果。上述四种数据处理方式计算得到的测深曲线结果并不完全一致。一般来说，远参考处理的测深曲线相比单点处理效果要好，其前提条件是对参考站的数据质量要求较高，需要在弱/无噪声干扰的环境下进行布设，但是一般在进行分布式采集时，各个采集站的数据质量事先不能预估，所以可能会出现远参考处理之后的测深曲线还不如单点处理的情况，同样的情况可能会发生在基于磁场相关远参考处理和共用磁道处理方法上。所以如何定量评价某特定采集站所计算的四种结果孰优孰劣，筛选出质量最好、最合理的测深曲线，是获得本地可靠电性结构模型的重要保证。

为了筛选出可靠的测深曲线，现有技术中是利用人工筛选的方式进行优选，具有一定的主观性且效率低，而如何定量筛选出能表征地下电性结构的测深曲线是需要研究的问题。

技术实现要素：

本发明所要解决的技术问题是为了克服现有技术的上述缺点，提供一种大地电磁测深曲线的定量优选方法，无需人工筛选，能够定量筛选出能表征地下电性结构的测深曲线，提高处理效率，增强优选的客观性及结果的准确性。

本发明解决其技术问题所采用的技术方案是：一种大地电磁测深曲线的定量优选方法，采用n台大地电磁测深仪分别对n个测深点进行分量数据采集，包括以下步骤：

a.每个测深点利用常规单点张量阻抗估算处理方式、远参考处理方式、基于磁场相关远参考处理方式、磁场共用处理方式中的至少两种进行分布式数据处理，得到每种处理方式后的测深曲线，并记录每一组测深曲线的频点个数；

b.计算任意两组测深曲线中视电阻率相互之间的离散弗雷歇距离以及抗相位相互之间的离散弗雷歇距离，离散弗雷歇距离按照下式计算：设两条测深曲线p和q，其频点个数分别为m和n，则p和q的离散弗雷歇距离为：

其中p:[0:m]→v，p是从集合[0:m]＝{0,1,...,m}到空间v的一个映射，α:[1:m+n]→[0,m]，α是从集合[1:m+n]＝{1,2,...,m+n}到集合[0:m]＝{0,1,...,m}的一个映射，α(k),k＝1,2,...m+n表示映射α在自变量取k时的映射值；q:[0:n]→v，q是从集合[0:n]＝{0,1,...,n}到空间v的一个映射，β:[1:m+n]→[0,n]，β是从集合[1:m+n]＝{1,2,...,m+n}到集合[0:n]＝{0,1,...,n}的一个映射，β(k),k＝1,2,...m+n表示映射β在自变量取k时的映射值，表示算子的复合运算，||·||2表示欧几里得距离；ψm,n是由两个连续、不减且满射算子构成的所有可能组合，

ψm,n＝mon([1:m+n],[0:m])×mon([1:m+n],[0:n])(2)

式(2)中，mon(x,y)是由集合x到集合y中连续、不减且满射的算子所构成，[1:m+n]＝{1,2,…,m+n}，[0:m]＝{0,1,…,m}，[0:n]＝{0,1,…,n}；

按照上述计算过程计算本地站b和其他采集站rj的视电阻率弗雷歇距离(b,rj)和阻抗相位的弗雷歇距离(b,rj)，其中，i表示xy或者yx方向，j＝1,…,n，n为测深曲线组数；

c.将离散弗雷歇距离计算结果加权，得到本地站和其他采集站测深曲线的离散弗雷歇距离：

其中，i表示xy或者yx方向，j＝1,…,n，n为测深曲线组数，l和d为加权因子；

d.筛选出δf(b,rj)最小者，得到该测深曲线即为最光滑合理的测深曲线。

具体的，所述分量数据采集包括5分量采集与4分量采集，其中，5分量包括电场2分量，磁场3分量；4分量包括电场2分量，磁场2分量。

具体的，步骤a中常规单点张量阻抗估算处理方式利用本地站的电场数据和磁场数据进行处理得到1组处理结果，远参考处理、基于磁场相关远参考处理利用其它n-1个采集站的磁场数据和本地站的电磁场数据进行处理分别得到n-1组处理结果；磁场共用处理方式利用本地电场数据和其它n-1个采集站的磁场数据来进行处理，得到n-1组处理结果。

优选的，l和d的范围分别为[0,1]。

本发明的有益效果是：利用离散弗雷歇距离来定量、自动筛选测深曲线，以克服现有技术中人工筛选测深曲线时主观性强、耗时久、效率低下，且无定量指标的缺点，具体而言是，利用离散弗雷歇距离来定量评价分布式数据处理后的多组测深曲线，离散弗雷歇距离利用两个目标的路径所形成的两条曲线上所有离散点的距离，测量两条曲线的相似度，而后筛选出分布式处理后的测深曲线的最优结果；该方法节省人力成本，筛选出能表征地下电性结构的测深曲线，提高结果客观性与准确性，提高处理效率，使用范围较广。本发明适用于筛选测深曲线。

附图说明

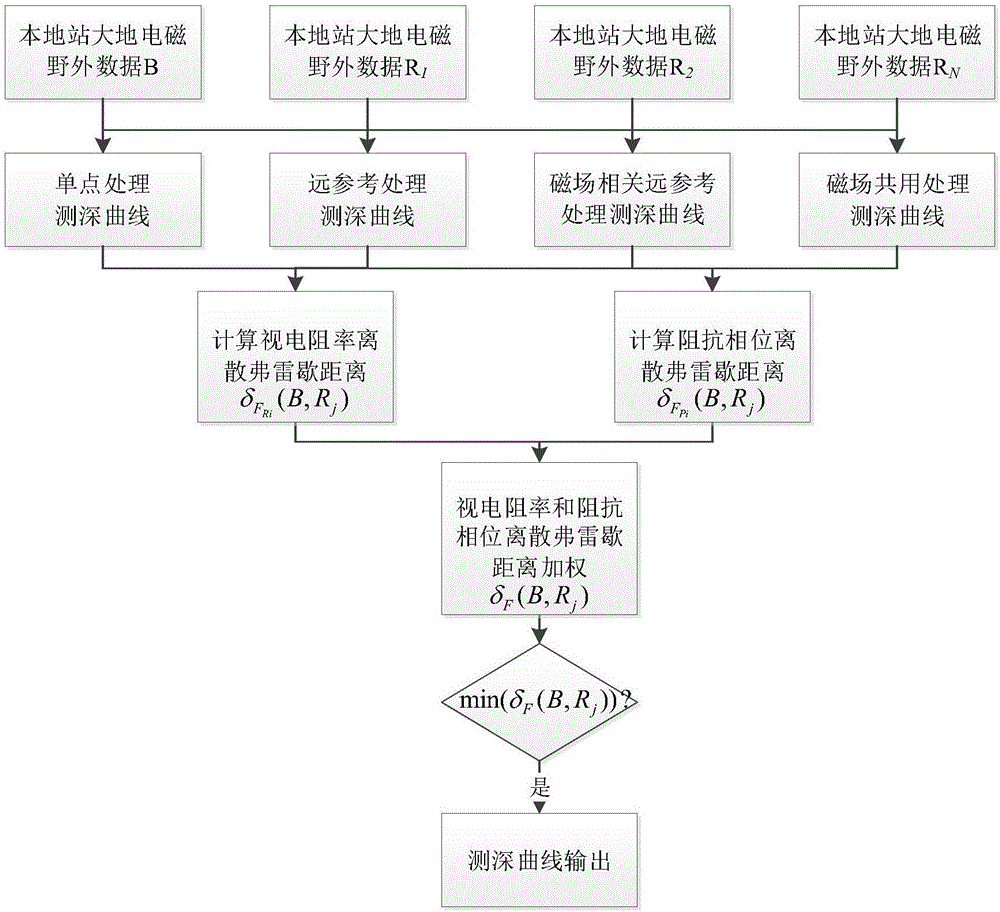
图1是本发明的流程示意图；

图2为正演测深曲线分别添加gauss、rayleigh、f分布、对数正态分布、poisson5种噪声后的结果；

图3为l39测点分布式数据处理后的7组测深曲线。

具体实施方式

下面结合附图及实施例，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明的一部分实施例，而不是全部的实施例。以下对至少一个示例性实施例的描述实际上仅仅是说明性的，决不作为对本发明及其应用或使用的任何限制。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。本发明未详细阐述部分属于本领域公知技术。

对于相关领域普通技术人员已知的技术、方法和设备可能不作详细讨论，但在适当情况下，所述技术、方法和设备应当被视为授权说明书的一部分。

如图1所示，本发明的大地电磁测深曲线的定量优选方法，包括以下步骤：

(1)采用n台大地电磁测深仪分别对n个测深点进行分量数据采集，本领域中常用的是5分量采集或4分量采集，即所述分量采集包括5分量采集与4分量采集，其中，5分量包括电场2分量，磁场3分量；4分量包括电场2分量，磁场2分量；

(2)每个测深点利用常规单点张量阻抗估算处理方式、远参考处理方式、基于磁场相关远参考处理方式、磁场共用处理方式中的至少两种进行分布式数据处理，得到每种处理方式后的测深曲线，并记录每一组测深曲线的频点个数；

常规单点张量阻抗估算处理方式是利用本地站的电场数据和磁场数据进行处理得到1组处理结果，远参考处理、基于磁场相关远参考处理利用其它n-1个采集站的磁场数据和本地站的电磁场数据进行处理分别得到n-1组处理结果；磁场共用处理方式利用本地电场数据和其它n-1个采集站的磁场数据来进行处理，得到n-1组处理结果。

在以下实施例中，为了选出最优的测深曲线，都是用了四种处理方式进行处理，而后进行筛选比较。在实际操作中，可以任意选择大于1的若干种处理方式进行筛选。则在同时选择上述四种处理方式时，共可得到3n-2组测深曲线。

(3)计算上述任意两组测深曲线中视电阻率相互之间的离散弗雷歇距离，以及各组阻抗相位相互之间的离散弗雷歇距离。当采用四种处理方式时，即计算3n-2组测深曲线中相关参数的离散弗雷歇距离。

离散弗雷歇距离按照下式计算：设两条测深曲线p和q，其频点个数分别为m和n，则p和q的离散弗雷歇距离(sriraghavendraetal,2007)为：

其中p:[0:m]→v，p是从集合[0:m]＝{0,1,...,m}到空间v的一个映射，α:[1:m+n]→[0,m]，α是从集合[1:m+n]＝{1,2,...,m+n}到集合[0:m]＝{0,1,...,m}的一个映射，，α(k),k＝1,2,...m+n表示映射α在自变量取k时的映射值；q:[0:n]→v，q是从集合[0:n]＝{0,1,...,n}到空间v的一个映射，β:[1:m+n]→[0,n]，β是从集合[1:m+n]＝{1,2,...,m+n}到集合[0:n]＝{0,1,...,n}的一个映射，β(k),k＝1,2,...m+n表示映射β在自变量取k时的映射值，表示算子的复合运算，||·||2表示欧几里得距离；

ψm,n＝mon([1:m+n],[0:m])×mon([1:m+n],[0:n])(2)

ψm,n是由两个连续、不减且满射算子构成的所有可能组合，如α1,α2,α3是mon([1:m+n],[0:m])中的元素，β1,β2是mon([1:m+n],[0:n])中的元素，则ψm,n＝{(α1,β1),(α1,β2),(α2,β1),(α2,β2),(α3,β1),(α3,β2)}。式(2)中，mon(x,y)是由集合x到集合y中连续、不减且满射的算子所构成，[1:m+n]＝{1,2,…,m+n}，表示从1到m+n的整数集，且1≤m+n；[0:m]＝{0,1,…,m}，表示从0到m的整数集，且0≤m；[0:n]＝{0,1,…,n}，表示从0到n的整数集，且0≤n，m和n分别为测深曲线p和q的频点个数，根据不同大地电磁方法，一般取值40-100，也和频点的疏密程度有关。

按照上述计算过程计算本地站b和其他采集站rj的视电阻率弗雷歇距离(b,rj)和阻抗相位的弗雷歇距离(b,rj)，其中，i表示xy或者yx方向，j＝1,…,n，n为测深曲线组数。

(4)将离散弗雷歇距离计算结果加权，得到本地站和其他采集站测深曲线的离散弗雷歇距离：

其中，i表示xy或者yx方向，j＝1,…,n，n为测深曲线组数，l和d为加权因子,l和d的范围为[0,1]，基于最优化考虑，取l＝0.6，d＝0.4

(5)筛选出δf(b,rj)最小者，得到该组测深曲线即为最光滑合理的测深曲线，获得最优的测深曲线并输出。

该方法基于离散弗雷歇距离，定量筛选分布式数据处理后的多组测深曲线，避免了利用人工筛选的主观性和费时费力的弊端。

实施例1

理论模拟，主要是说明方法的正确性，利用此方法能够筛选出最优的曲线。一般，地球物理勘探领域有一个新方法提出，首先需要进行理论模型验证，然后再推广到实际中去。

本例为理论模拟计算，都以四种处理方式进行处理，利用上述的大地电磁测深曲线的定量优选方法包括如下步骤：

(1)建立层状模型：在0-100km深度电阻率为1000ω·m的背景下，5-20km深度为10ω·m的低阻异常，得到正演后的测深曲线如图2黑色实线所示。

(2)为了模拟各种干扰引起的测深曲线异常，在原始测深曲线中添加5种噪声，分别是：高斯分布(gauss)噪声、瑞利分布(rayleigh)噪声、f分布噪声、对数正态分布噪声、泊松(poisson)噪声，得到多组测深曲线如图2中离散点所示；

(3)计算上述6组测深曲线中视电阻率相互之间的离散弗雷歇距离(b,rj)，以及6组测深曲线中阻抗相位相互之间的离散弗雷歇距离(b,rj)，计算离散弗雷歇距离如公式(1)所示；

(4)将离散弗雷歇距离进行加权，加权计算过程如公式(3)，得到的加权结果如表1所示；

表1正演测深曲线与加噪后每组测深曲线的弗雷歇距离加权值

(5)筛选出加权离散弗雷歇距离δf(b,rj)中的最小者，得到该组测深曲线即为最光滑合理的测深曲线。经计算，原始正演后测深曲线与其他组的离散弗雷歇距离为26.54，为最小，由此从6组测深曲线中挑选正演后测深曲线作为最终结果。

理论计算结果证明了利用离散弗雷歇距离自动筛选测深曲线的正确性。

实施例2

本例为实际野外资料，一种大地电磁测深曲线的定量优选方法，l33、l36、l39为位于跨龙门山构造带南西段进行同步观测的三个大地电磁测深点，为了从l39测点分布式处理结果中筛选出最优的一组测深曲线，包括如下步骤：

(1)对于l39测点，利用四种处理方式进行分布式数据处理，具体而言，常规单点张量阻抗估算处理(l39ss)处理出一组测深曲线，利用l33、l36对l39测点进行远参考处理(l39vsl33_rr，l39vsl36_rr)处理出2组测深曲线、磁场相关远参考处理(l39vsl33_rrhc，l39vsl36_rrhc)处理出2组测深曲线、磁场共用处理(l39vsl33_uh，l39vsl36_uh)处理出2组测深曲线，共得到7组测深曲线，如图3所示；

(2)计算上述7组测深曲线中视电阻率相互之间的离散弗雷歇距离，以及7组阻抗相位相互之间的离散弗雷歇距离。离散弗雷歇距离按照(1)式计算；

(3)将离散弗雷歇距离进行加权，加权计算过程如公式(3)，得到的加权结果如表2所示；

表2l39与l33、l36的分布式数据处理后每组弗雷歇距离的加权值

(4)筛选出加权离散弗雷歇距离δf(b,rj)中的最小者，该组测深曲线即为最光滑合理的测深曲线。经计算，7组测深曲线中，远参考处理l39vsl33_rr与其他组测深曲线的离散弗雷歇距离为122.74，为最小，由此选择远参考处理后的结果为最终结果。

本发明使用范围较广，利用天然电磁场勘探的音频大地电磁法(amt)、宽频大地电磁法(mt)和长周期大地电磁法(lmt)皆可使用。