一种基于空频自适应滤波的卫星导航抗干扰方法与流程

本发明属于卫星导航抗干扰技术领域，具体涉及一种空频自适应的信号处理方法。

背景技术：

卫星信号到达地面时只有-130dbm，极易受到干扰。在复杂的电磁环境下，卫星导航的脆弱性成为制约其持续稳定定位的主要因素。卫星导航抗干扰技术，利用方向图可控天线阵(crpa)，实时自适应地生成空域滤波权矢量，并做加权处理，使抗干扰天线在空间来向未知的干扰方向自适应地形成零陷，或在卫星信号入射方向形成增益，获得良好的信噪比。这对于战时复杂电磁环境下惯性/卫星组合导航的生存能力，有至关重要的意义。因为干扰个数、带宽、时变性各不同，对抗干扰阵列天线的自由度、各通道的一致性及抗干扰算法的运算速度都有严苛要求，因此抗干扰算法及其高效实现成为卫星导航专业中非常复杂和必要的研究方向。

技术实现要素：

发明目的：

针对卫星导航易受干扰的问题，提出一种空域自适应滤波的数字信号处理方法，实现卫星导航抗干扰的功能。

技术方案：

第一方面，提出了一种基于空频自适应滤波的卫星导航抗干扰方法，其特征在于，包括:

接收m个阵元的中频数据；

在每个阵元的中频数据中，每n个点形成一个数据段，对每个数据段进行汉明窗加窗处理得到加窗数据段；

将每个加窗数据段的后25％×n点数据与后一加窗数据段的前25％×n点数据相加并用加和之后的数据替换所述当前加窗数据段的后25％×n点数据得到重叠数据段；

对每个重叠数据段进行n点快速傅立叶变换得到对应的频点数据；

将所述频点数据缓存在双口ram中；

利用所述频点数据，计算与所述频点数据中的每个数据段中的前13个频点以及后13个频点对应的协方差矩阵；

对所述协方差矩阵进行自适应对角加载得到加载矩阵；

对所述加载矩阵进行求逆得出逆矩阵；

利用逆矩阵，根据线性约束最小方差准则求得所述频点数据的最优权值；

从所述双口ram中读取所述频点数据；

利用所述最优权值对所述频点数据进行加权处理得到加权数据；

对加权数据进行逆快速傅立叶变换并输出处理结果，其中，所述m和n均为自然数。

可选地，对所述加载矩阵进行求逆是利用fpga对所述加载矩阵进行求逆。

可选地，所述协方差矩阵是二阶的。

可选地，对所述协方差矩阵进行自适应对角加载是指对每个协方差矩阵，自适应地加上第一行第一列数据除以8192的数值。

可选地，其中根据线性约束最小方差准则求得所述频点数据的最优权值包括对所述频点数据中的每个数据段中的第14至第n-13个频点的权值取零。

可选地，所利用的最优权值是与其进行加权处理的频点数据计算得到。

可选地，所述n为64。

第二方面，提出了一种基于空频自适应滤波的卫星导航抗干扰装置，其特征在于，包括：

接收模块，用于接收m个阵元的中频数据；

加窗模块，用于在每个阵元的中频数据中，每n个点形成一个数据段，对每个数据段进行汉明窗加窗处理得到加窗数据段；

叠加模块，用于将每个加窗数据段的后16点数据与后一加窗数据段的前16点数据相加并用加和之后的数据替换所述当前加窗数据段的后16点数据得到重叠数据段；

变换模块，用于对每个重叠数据段进行n点快速傅立叶变换得到对应的频点数据；

存储模块，用于将所述频点数据缓存在双口ram中；

协方差矩阵计算模块，用于利用所述频点数据，计算与所述频点数据中的每个数据段中的前13个频点以及后13个频点对应的协方差矩阵；

对角加载模块，用于对所述协方差矩阵进行自适应对角加载得到加载矩阵；

求逆模块，用于对所述加载矩阵进行求逆得出逆矩阵；

最优权值计算模块，用于利用逆矩阵，根据线性约束最小方差准则求得所述频点数据的最优权值；

读取模块，用于从所述双口ram中读取所述频点数据；

加权处理模块，用于利用所述最优权值对所述频点数据进行加权处理得到加权数据；

逆变换模块，用于对加权数据进行逆快速傅立叶变换并输出处理结果

有益效果：

相较于传统的时域l抽头的空时自适应处理stap，本发明将lm×lm维矩阵运算降至2m×2m维矩阵，减小了运算量，提高了运算实时性，其中m是天线阵元数量。同时，对部分频点的弃用，运算实时性进一步提高。并且，因为二阶fft、时域加窗和重叠的引入，缓解了现有sfap零限杂乱的问题。第三，自适应对角加载的引用提高了抗干扰处理的数值稳健性，抗干扰性能得到提高。

附图说明

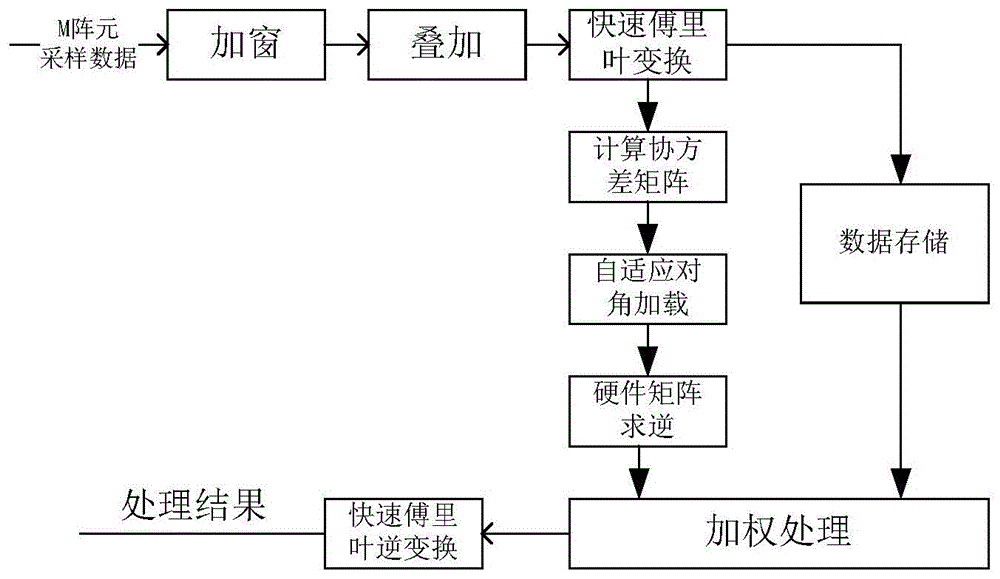
图1是本发明方法的流程图。

具体实施方式

下面结合附图对本发明进行详细描述

本发明采用二阶空频自适应处理(spacefrequencyadaptiveprocessing,sfap)方法，通过fft(快速傅里叶变换)将输入信号划分为n个频点，并在每个频点上采用矩阵求逆的方法计算各个阵元的最优权值。缓存fft后的数据，与该数据计算出的最优权值做加权处理，再进行ifft(快速傅里叶逆变换)后达到抑制干扰的目的。

假设阵列有m个阵元，每个频点的操作在2m×2m维矩阵中进行，包括协方差矩阵的统计平均计算、矩阵求逆和权值归一化三个数字信号处理步骤。本发明选取n＝64，为减小运算量，提高抗干扰实时性，只计算前13个频点和后13个频点的最优权值，其余频点的最优权值取零。

同时，为减少频谱泄漏带来的影响，除采用二阶fft以外，本发明采用时域加窗和25％叠加的方法，使宽带干扰达到理想中的均匀分割，缓解了sfap比stap(spacefrequencyadaptiveprocessing)零限较杂乱的问题。

而且，当干扰较大时，各阵元间的自适应矩阵病态度高，数值稳健性差。本发明采用对协方差矩阵进行自适应对角加载的方法，降低矩阵求逆的误差，提高抗干扰性能。

具体步骤如下：

1)对m个阵元的中频采样处理，选择合适的n点，本设计n＝64。每n个点形成一个数据段，对每个数据段进行hamming窗加窗处理得到加窗数据段；

2)相邻的每个数据段做25％重叠。即把每个数据段的最后25％×n点数据和下一段数据的前25％×n点数据重叠相加，并用加和之后的数据替换当前加窗数据段的后25％×n点数据；

3)对个数据段做n点fft得到对应的频点数据；

其中m＝1,2,……m，k＝1,2,……n.

xm(n)为对应的时域中，第m个阵元后的第n个采样值，ωn是时域窗函数的第n个系数，而xm(k)为频域中第m个阵元后的第k个采样值。

4)将频点数据缓存在双口ram中；

5)计算协方差矩阵；

m个阵元组成的第k个频点的矢量为：

x(k)＝(x1(k),x2(k),……xm(k))^t,增加为二阶矢量得到：

x’(k)＝(x1(k),x1(k+1),x2(k),x2(k+1),……xm(k),xm(k+1))^t，

协方差矩阵为r(k)＝e{x’(k)x’^h(k)}，是一个2m×2m维矩阵。期望的实现形式是对170个协方差矩阵的统计平均。为简化运算，只计算k＝[1…13]和k＝[52…64]区间内的协方差矩阵。

6)取出每个频点协方差矩阵的第一行第一列数据，将其除以8192，将结果与该协方差矩阵对角线上的元素相加；

7)对协方差矩阵进行fpga硬件矩阵求逆，并根据线性约束最小方差准则(lcmv)，求得k＝[1…13]和k＝[52…64]频点的最优权值；

其中k＝1,2,……13,52,53,……,64。

u(k)是信号从期望方向入射时，在第k个频点形成的导向矢量，最优权值h(k)是一个2m维矢量。

8)取步骤4中ram中的数据，与7步骤计算得到的权值做加权处理。注意时序控制，确保利用的最优权值是与其进行加权处理的频点数据计算得到。

其中k＝1,2,……13,52,53,……,64。