基于盲源分离的压力容器声发射信号检测的方法与流程

本发明属于压力容器声发射信号检测的信号处理领域，涉及基于盲源分离的压力容器声发射信号检测的方法。

背景技术：

压力容器是在石油化工、医药、食品等行业领域中广泛使用的设备，属于工业生产和人民日常生活的重要基础设施。由于这些设备大多盛装高温、高压、易燃、易爆或剧毒介质，压力容器一旦发生开裂或泄漏，往往并发爆炸、火灾或中毒等灾难性事故，造成人民生命财产的重大损失，并引起严重环境污染，社会影响恶劣。

为了保证压力容器的使用的安全性和规范性，各种无损检测技术在压力容器的制造和在役定期检验中得到广泛应用，现有的无损检测方法有声发射检测、射线检测、超声检测、磁粉检测和渗透检测等常规无损检测方法。但磁粉以及渗透等方法需要停产检验，超声检测或射线探伤方法探测到的能量来自无损检测仪器，不适合长期连续的检测，而声发射检测属于一种动态检测方法，可以提供缺陷随着环境变化的实时连续信息，并且能够快速检测大型构件，以及检测危害结构安全的活动性缺陷，提供缺陷动态信息。

声发射信号属于非线性、非平稳的检测信号，目前常用的压力容器的声信号检测方法有人工检测法、反向传播神经网络(bpnn)、ds融合和支持向量机等方法。然而bpnn方法存在收敛速度过慢的问题，并且容易陷人局部最优；ds融合方法通常在识别过程中无法获得大量的样本数据。

由于压力容器设备属于工业广泛且长期使用的设备，声发射信号的检测是分析容器是否产生泄漏的第一步，用传统检测方法可能存在生产过程中无法及时检测的情况，极可能导致人员和财产的重大损失，这对未来在线检测指明了方向。因此及时并准确地在线检测出压力容器声发射信号，对防止事故发生，保证人员和财产的安全具有重要意义。

技术实现要素：

有鉴于此，本发明的目的在于提供一种基于稀疏表示的盲源分离的压力容器测漏的声发射检测的方法。本方法通过构建盲源分离(bbs)模型，建立观测信号与声源信号的关系模型，利用短时傅里叶变换(stft)将时域信号转换为时频信号，然后根据声信号的稀疏性，并进行单源点检测，利用改进拉普拉斯势函数对单源点进行聚类，得出盲源分离模型的混合矩阵。最后，根据混合矩阵利用最小化l1范数还原源声信号。

为达到上述目的，本发明的技术方案提供一种基于稀疏表示的盲源分离的压力容器测漏的声发射检测的方法，所述方法包括以下步骤：

1)通过安装在压力容器上的声发射传感器采集通过激励产生的泄露、噪声和正常的声发射信号，再对采集的数据进行预处理。

2)建立观测信号(即声发射传感器采集信号)与声源信号的bbs模型，其中观测信号个数已知，声源信号个数未知。

3)对bbs模型进行短时傅里叶变换，对变换之后的信号进行单源点检测，去掉低能量的点，并做归一化处理。

4)利用改进拉普拉斯势函数进行聚类处理，并找出聚类中心，求出混合矩阵。

5)根据混合矩阵利用最小l1范数法还原声源信号。

本发明达到的有益效果为：本发明提出了一种基于盲源分离的压力容器的声发射检测的方法。该方法可以根据已知的观测信号还原出未知的发声源信号的个数以及特征。通过短时傅里叶变换(stft)对信号进行处理以及单源点检测这种去噪策略的引入，能够充分利用声信号的稀疏性，并利用改进拉普拉斯势函数对信号进行聚类，能够轻松地找到聚类中心。运用最小化l1范数还原声信号，在计算上便于实现。该方法克服了人工检测方法速度慢以及传统方法特征的提取依赖人工经验的缺点，使还原得到的声信号更加的准确。

附图说明

为了使本发明的目的、技术方案和有益效果更加清楚，本发明提供如下附图进行说明：

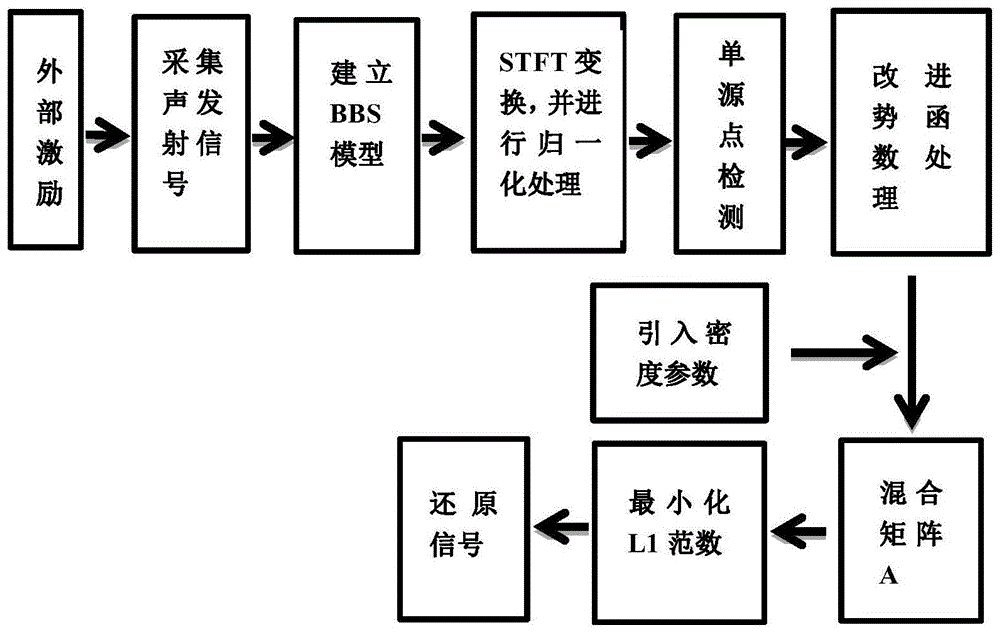
图1为本发明所述基于盲源分离的压力容器声发射信号检测的方法的实施流程框图。

图2为本发明所述bbs模型。

具体实施方式

为了更清楚地说明本发明的目的、技术方案和优点，下面结合附图对本发明的方法做描述，附图1为本发明的基于盲源分离的压力容器声发射信号检测的方案的流程框图，具体实施的步骤如下：

1)通过安装在压力容器上的声发射传感器采集通过激励产生的泄露、噪声和正常的声发射信号，再进行数据预处理。

首先在压力容器各关键位置安装好统一规格的声发射传感器，通过施加激励的方式模拟泄露和噪声发生时的声发射信号，来获取需要的声发射数据，数据的种类和激励方式如下表1所示。本发明将压力容器现场常检测到的声发射源分为正常、泄露信号、干扰信号三种，正常数据直接采集正常的情况下的声发射信号，泄露的声发射数据可以通过打开压力容器的阀门来产生，用0.5mm的hb铅笔芯来断铅以模拟压力容器开裂的声信号，摩擦信号就通过用不同材料摩擦压力容器获取，水滴信号通过往压力容器滴水的方式模拟，电磁噪声则采用在一旁运行大功率电机来实现，至于复合干扰则将各类噪声信号交叉组合在一起来采集声发射信号。

表1压力容器各类声发射源激励方式表

2)获取了声发射数据后,建立bbs模型,如式(1)所示。

其中观测信号为x1(t)，x2(t)，…，xm(t)，m为已知的观测信号个数，源声源信号为s1(t)，s2(t)，…，sn(t)，n为未知的发声源信号个数。a为bbs模型的混合矩阵，噪声信号为n1(t)，n2(t)，…，nn(t)。

这个过程形一般可以看作为两个系统，对于把源信号通过混合矩阵进行混合并加入一些噪声干扰得到混合后的观测信号这一过程可以被看作为混合系统。对于利用混合后得到的观测信号对混合矩阵估计进而对源信号进行恢复，最终得到分离出的源信号这一过程可以被看作是盲源分离系统，如附图2所示。

3)为了得到更好的稀疏性，用短时傅里叶变换进行处理。那么可知第i个混合信号可以写为：

第n个声源信号为：

其中win(·)是窗函数，一般加窗函数可以为汉明窗。

那么时频域下的混合信号可以改写为：

x(t，f)＝as(t，f)(4)

其中x(t，f)＝[x1(t，f)，x2(t，f)，…，xn(t，f)]^t是进行短时傅里叶变换后的混合信号，s(t，f)＝[s1(t，f)，s2(t，f)，…，sm(t，f)]^t是经过短时傅里叶变换后的源信号。对于短时傅里叶变换可以较好地利用语音信号的特性，同时可以较好的降低算法的复杂度，并且相较于傅里叶变换来说，短时傅里叶算法能更好地得到信号的瞬时频率的特性。

混合矩阵的估计计算主要是依靠信号的稀疏性，单源点检测能够提稀疏信号的聚类程度，并且能够有效去除杂波。单源点检测处理方式为任意两个信号满足式(5)的关系式。

其中ε是一个接近0的门限值。剩下的点即为单源点。单源点存在某一时刻t，有且只有一个源信号其主导作用，满足关系式(6)，观测信号具有线性聚类特征。

一般情况下散点周围除了会存在一些干扰点或者噪声外，离原点较近的一些低能量的点也会影响聚类效果。为了提高混合矩阵的估计精度，一般通过式(7)去掉一部分的低能量点。

||x(t，f)||＞λ·max||x(t，f)||(7)

式中，参数λ∈(0，1)。

为了更好地聚类，提高预估的矩阵的精度，还需要根据下式进行归一化的处理。

4)利用改进势函数进行聚类的具体步骤：

(1)引入密度参数，寻找初始聚类中心，已知数据点

x(t，f)＝[x1(t，f)，x2(t，f)，…，xn(t，f)]^t

任意两个数据点间的欧氏距离为：

d(x(i，f)，x(j，f))＝(|x1(i，f)-x1(j，f)|²+x2(i，f)-x2(j，f)|²+…+xm(i，f)-xm(j，f)|²)^1/2其中

x(i，f)＝[x1(i，f)，x2(i，f)，…，xn(i，f)]^t，

x(j，f)＝[x1(j，f)，x2(j，f)，…，xn(j，f)]^t

t个数据点的平均距离为

空间中任一点x(i，f)，以该点为中心半径为r的区域称为该点的邻域，邻域内的点的个数称为点x(i，f)基于距离r的密度参数，这里取r＝dm，则点x(i，f)的密度参数d(x(i，f))可表示为

其中

u(x)＝1，x≥0

u(x)＝0，x＜0

空间中任意一点x(i，f)，若其附近的点越多，d(x(i，f))则越大.故选择d(x(i，f))大的点作为初始聚类中心，有利于聚类过程的高效收敛.同时，为了避免所选的初始聚类中心局部收敛，在选取初始聚类中心时，尽可能使所选点之间的距离最大.因此，基于密度选取初始聚类中心算法的具体步骤如下：

i.计算t时刻观测数据点x(t，f)的密度参数d(x(t，f))，选取出的x(t，f)满足

其中ε1＝0.35，满足上式的数据点记作放入高密度点集合h中。在h中选择密度参数值最大的数据点作为第1个初始聚类中心，记为z1，取h中离z1最远的数据点作为第2个聚类中心z2，将z1和z2按列存放于初始聚类中心矩阵z中，并在h中将z1和z2删除。

ii.计算h中剩余的的数据点到x(t，f)到已知的初始的聚类中心{zh}的距离

iii.z3为h中满足的将z3并入z中，并在h中将z3删去。同理zk为h中满足

的如此循环，直至找出c个初始聚类中心，c的值可按t＞＞c＞m(t为采样点数,m为观测信号个数),这里取c＝5m。

(2)基于密度选取初始聚类中心的方法可用于势函数，来解决源信号个数未知的盲分离问题.为了正确估计势函数的各个局部最大值，可采用改进拉普拉斯势函数，如式(8)。

其中是观测矩阵处理之后的列向量，t为列数。当j(ok)取得局部最大值时，所对应的ok可近似作为观测数据的聚类中心。式中的参数b的值可用下式估计：

其中

要求解j(ok)的极大值可以先求导令导数值为0，然后采用固定点优化迭代算法，得到第l+1次迭代时第k个聚类中心的表达式(9)，即

其中l为迭代次数，l的初始取值为0，并令z3为得初始聚类中心矩阵z中的列矢量。当时，停止迭代.其中，ε为计算精度，其越接近0，精度越高，但算法的复杂度也增加，这里取ε＝10^-6。

当算法收敛后，聚类中心矢量ok将凝聚在j(ok)的各个局部最大值处。而在实际中，j(ok)的有些局部最大值是由噪声和异常值造成的，但噪声和异常值所产生的聚类中心对应的j(ok)值相对来说较小，故可按式(10)进行处理,

来消除噪声和异常值的影响，将不满足式(10)的ok剔除，最终保留下来的聚类中心个数即源信号的个数，聚类中心矢量即估计的混合矩阵的列矢量，这里ε的大小可凭经验选取，这里取ε＝0.5。所求得的n个ok组成的矩阵，即为所估计的混合矩阵am×n，其中m为观测信号个数，n为声源信号个数。

5)利用最小l1范数还原信号的具体步骤：

(1)对于已经估计出来的混合矩阵am×n，选取am×n当中任意m个列向量构成矩阵wm×m，其中该任意m列向量所对应的m个声源信号有值，而其他n-m个声源信号值估计为0。m个声源信号有值组成矩阵sm×1(t)。利用式子(11)

x(t)＝wm×m·sm×1(t)(11)

由于wm×m可逆，x(t)已知，则解出sm×1(t)，将am×n中所有m个列向量组合计算出所有可能的sm×1(t)，然后利用选则最小值作为原声源信号。

最后按这样的步骤，对t个时刻进行处理，这完成了0～t时刻的声源数据还原，完成基于盲源分离的声源信号检测。